
13 P
1st - Uni

21 P
9th - 12th

24 P
9th - 12th

10 P
12th
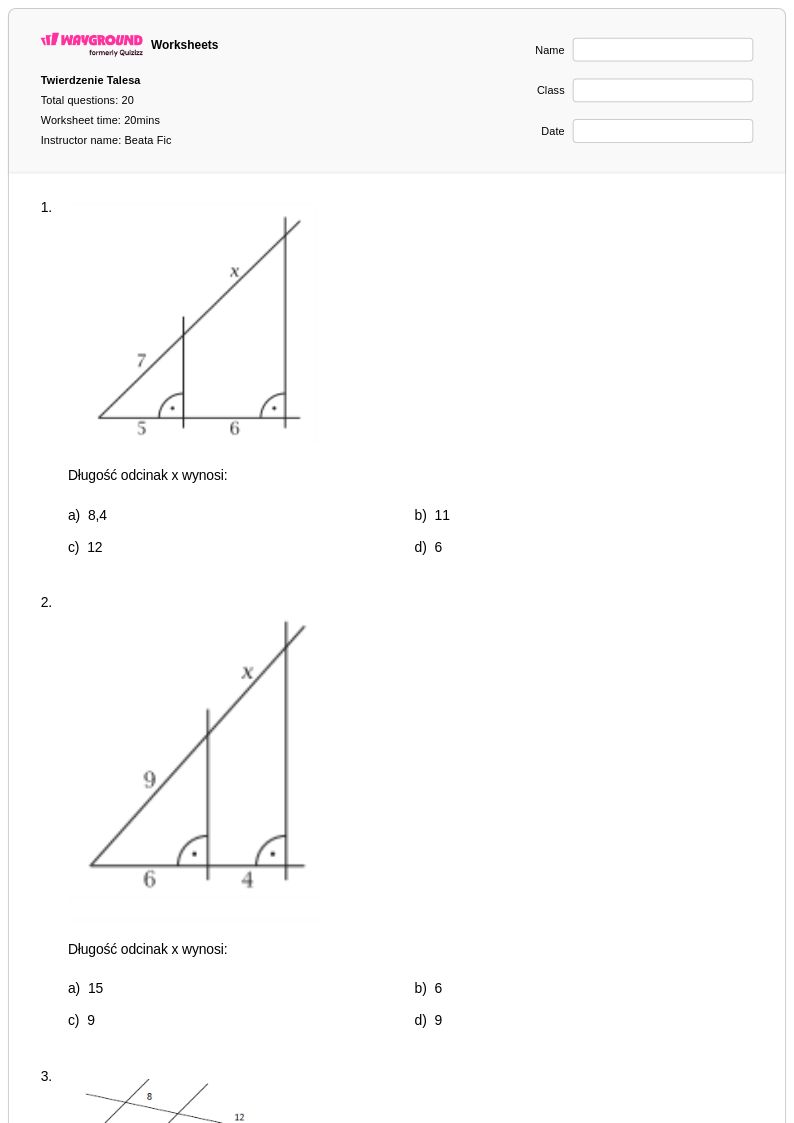
20 P
12th
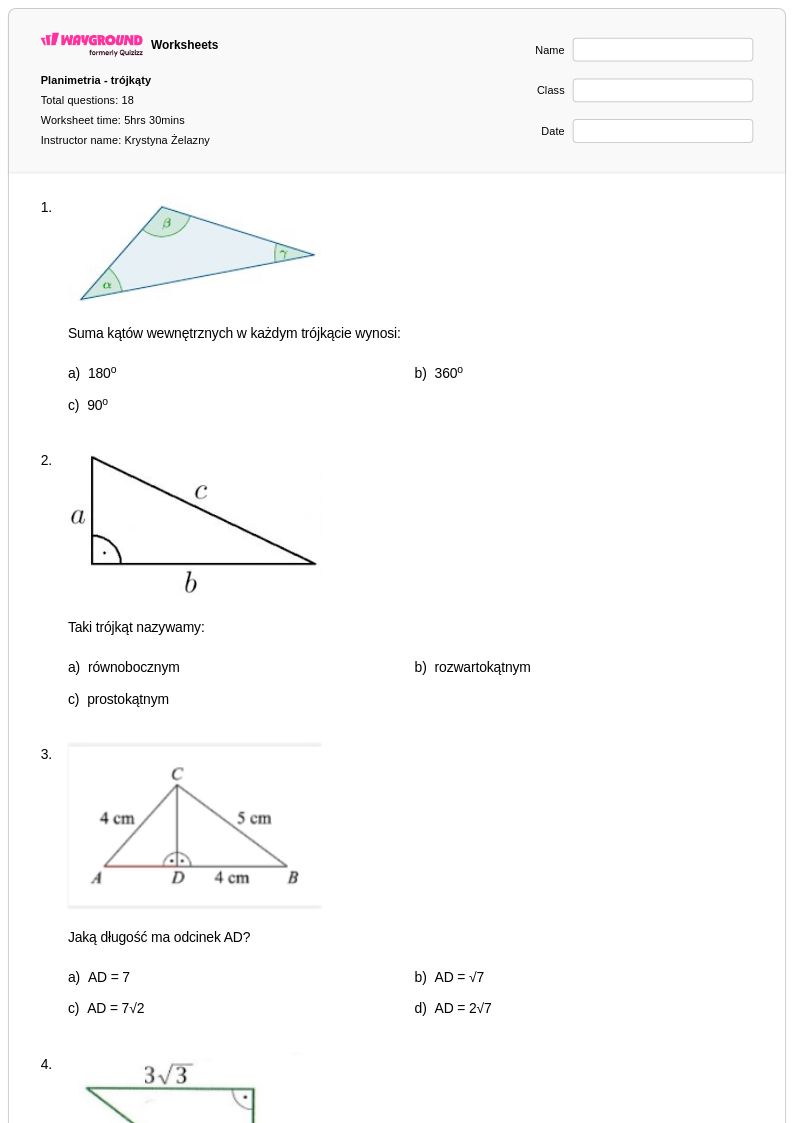
18 P
12th

11 P
12th
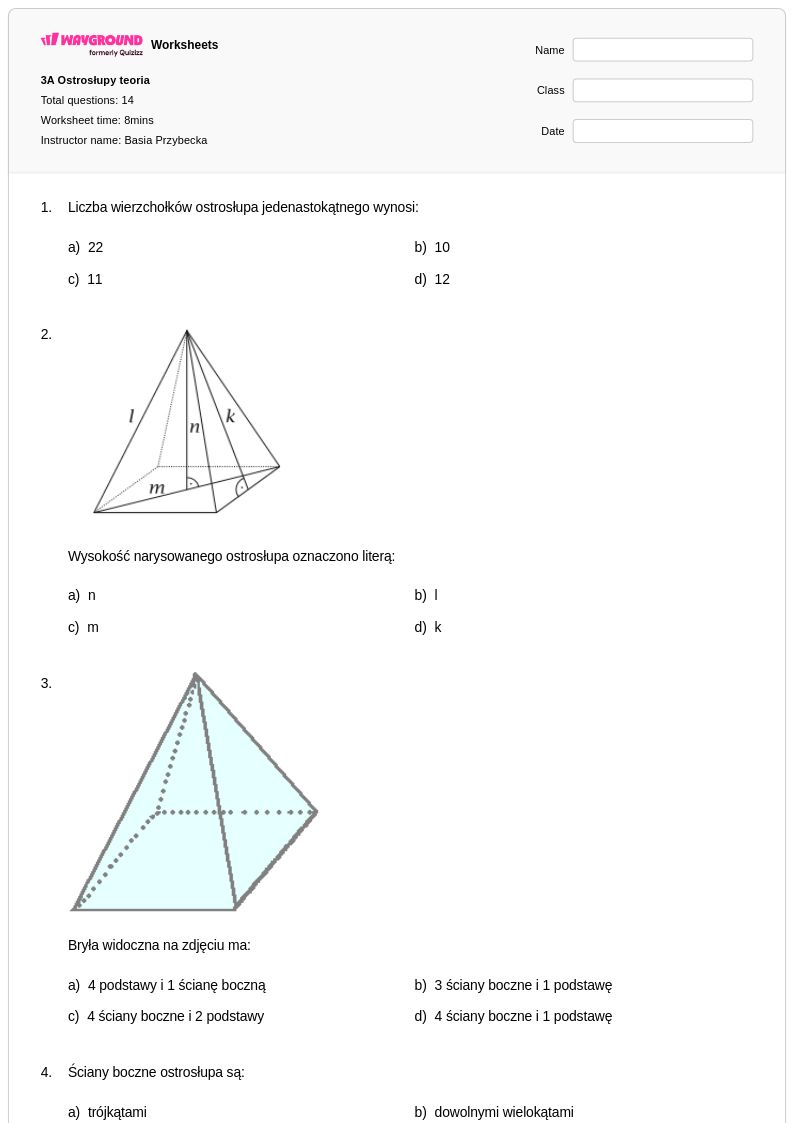
14 P
12th
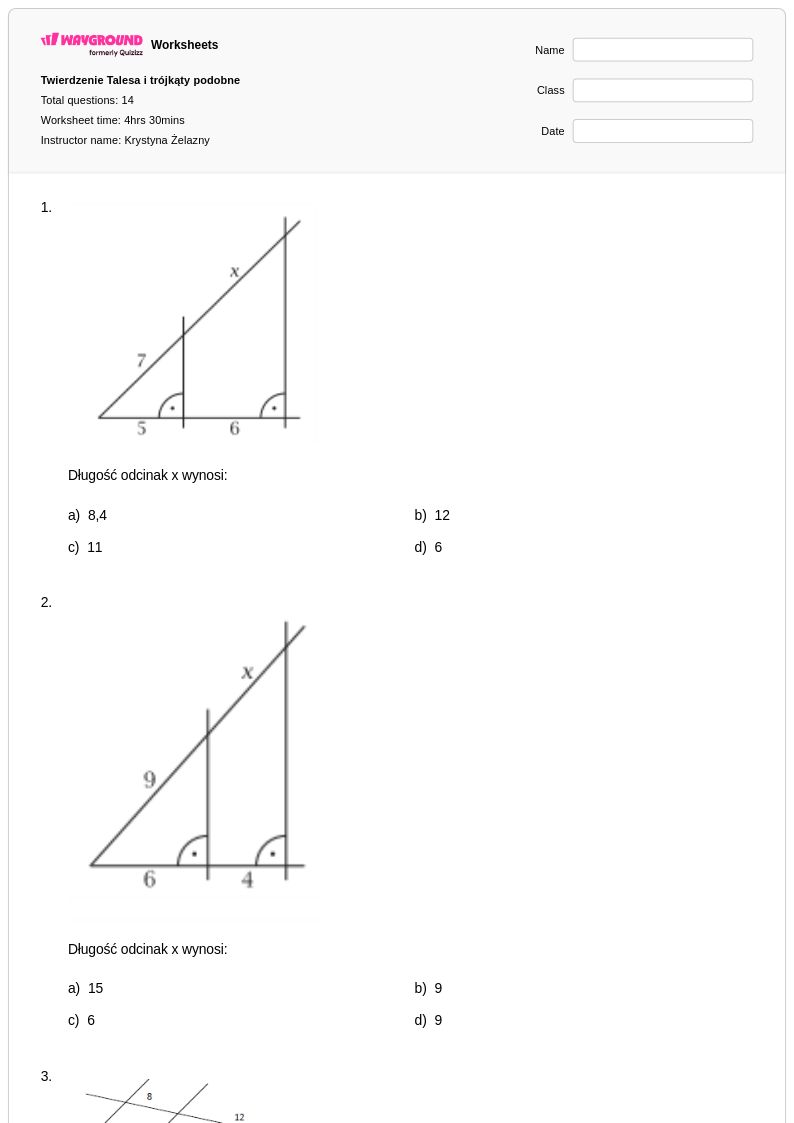
14 P
12th

8 P
8th - 12th

20 P
10th - 12th

12 P
12th
![[8] Cechy przystawania trójkątów - Nadający się do druku Twierdzenie-o-nierówności-trójkąta Karty-pracy Klasa 12 - Quizizz](https://quizizz-static.s3.amazonaws.com/_media/worksheets-new/65bfc9414f4f362db084f34b-[8]-cechy-przystawania-trójkątów)
10 P
8th - Uni

50 P
9th - 12th

12 P
9th - 12th

20 P
9th - 12th

13 P
9th - 12th

9 P
9th - 12th
20 P
9th - 12th

6 P
9th - 12th

21 P
12th

19 P
9th - 12th

10 P
9th - 12th

21 P
7th - PD
Przeglądaj Twierdzenie o nierówności trójkąta arkusze ćwiczeń według ocen
Przeglądaj inne arkusze tematyczne dla klasa 12
Przeglądaj arkusze Twierdzenie o nierówności trójkąta do wydrukowania dla Klasa 12
Arkusze ćwiczeń z twierdzenia o nierówności trójkątów dla uczniów klasy 12, dostępne w Wayground (dawniej Quizizz), zapewniają kompleksowe ćwiczenia z tą fundamentalną zasadą geometryczną, która reguluje relacje między długościami boków w trójkątach. Te starannie zaprojektowane arkusze ćwiczeń wzmacniają umiejętności analityczne uczniów, stawiając przed nimi wyzwanie: czy z trzech danych długości można zbudować trójkąt, zastosować twierdzenie do rozwiązania problemu nieznanych długości boków oraz przeanalizować dowody geometryczne dotyczące konstrukcji trójkątów. Uczniowie pracują nad systematycznie ustrukturyzowanymi zadaniami praktycznymi, które obejmują zarówno podstawowe zastosowania, jak i złożone scenariusze wieloetapowe. Każdy arkusz ćwiczeń zawiera szczegółowe klucze odpowiedzi, które wspierają samodzielną naukę i samoocenę. Bezpłatne materiały do druku oferują zróżnicowane formaty zadań, od ćwiczeń z weryfikacji numerycznej po zastosowania algebraiczne, w których uczniowie muszą znaleźć zakresy możliwych wartości boków trójkątów.
Obszerna kolekcja Wayground opiera się na milionach materiałów dotyczących twierdzenia o nierówności trójkątów, stworzonych przez nauczycieli, umożliwiając nauczycielom precyzyjne wyszukiwanie i filtrowanie materiałów dzięki rozbudowanym funkcjom wyszukiwania i filtrowania, które sortują je według poziomu trudności, rodzaju problemu i zgodności ze standardami matematycznymi. Nauczyciele korzystają z zaawansowanych narzędzi do różnicowania, które pozwalają dostosować złożoność arkuszy ćwiczeń do zróżnicowanych potrzeb uczniów, niezależnie od tego, czy zapewniają one pomoc uczniom mającym trudności w nauce, czy też stanowią wyzwanie dla uczniów zaawansowanych. Elastyczne opcje formatowania platformy obejmują zarówno zadania cyfrowe, jak i pliki PDF do pobrania i wydrukowania, usprawniając planowanie lekcji i umożliwiając płynną integrację z różnymi metodami nauczania. Te kompleksowe zbiory arkuszy ćwiczeń wspierają systematyczne budowanie umiejętności poprzez starannie opracowane zadania praktyczne, umożliwiając nauczycielom uzupełnianie indywidualnych luk w nauce, a jednocześnie utrwalanie znajomości tego istotnego twierdzenia geometrycznego w zróżnicowanych warunkach klasowych.
