15 คิว
7th

13 คิว
7th

10 คิว
7th

11 คิว
10th

35 คิว
10th

21 คิว
5th
20 คิว
9th - 12th
16 คิว
10th
14 คิว
6th - 8th

11 คิว
7th
20 คิว
10th
21 คิว
9th

15 คิว
6th

26 คิว
12th
16 คิว
12th
22 คิว
9th - 12th
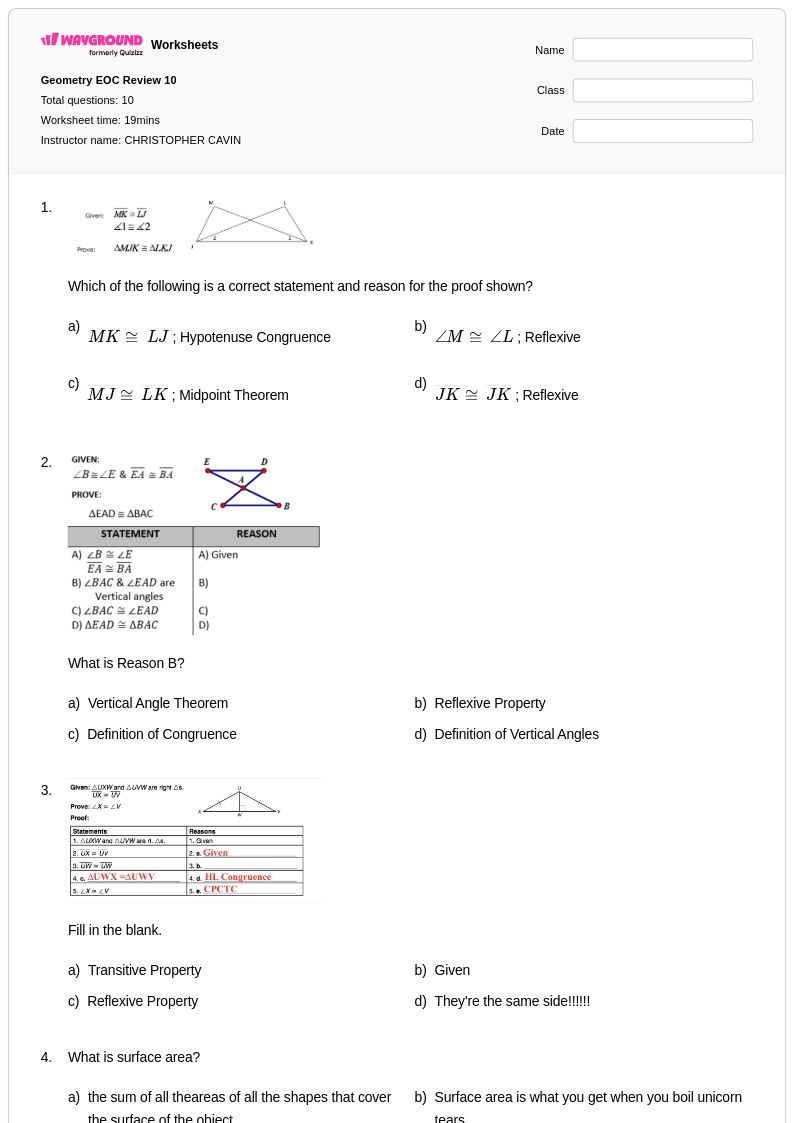
10 คิว
10th
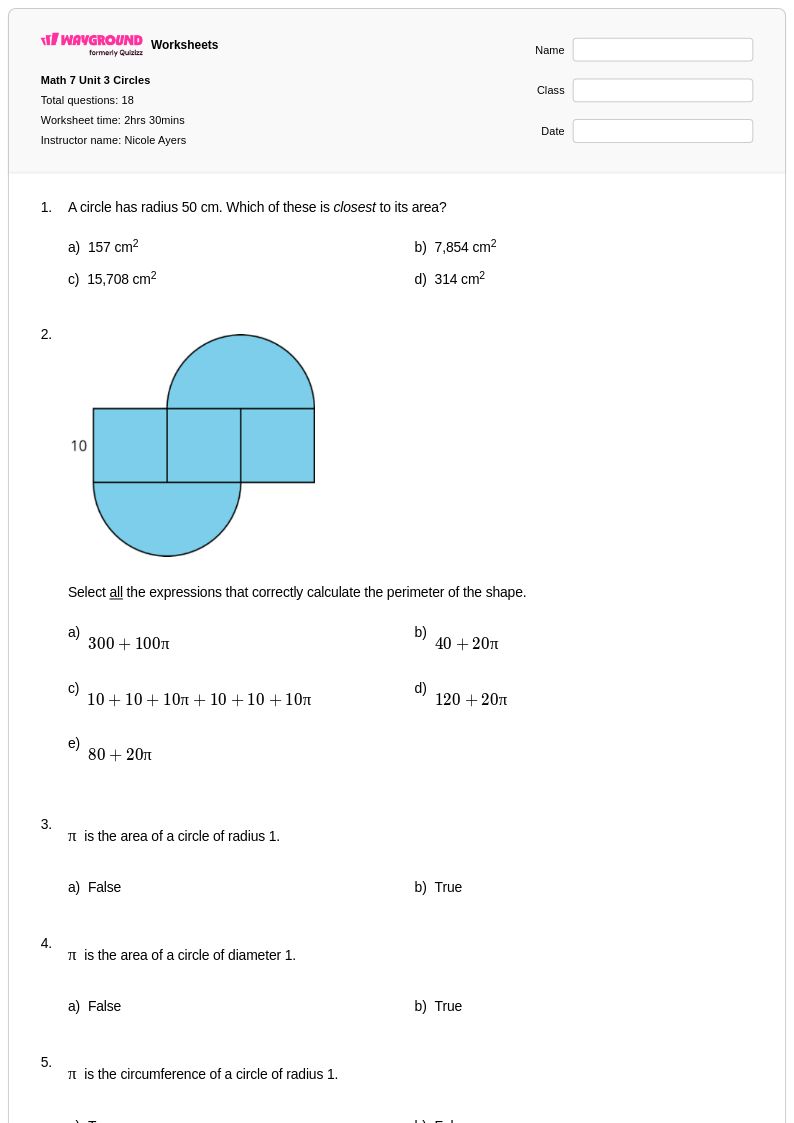
18 คิว
7th

14 คิว
7th

10 คิว
6th - 8th
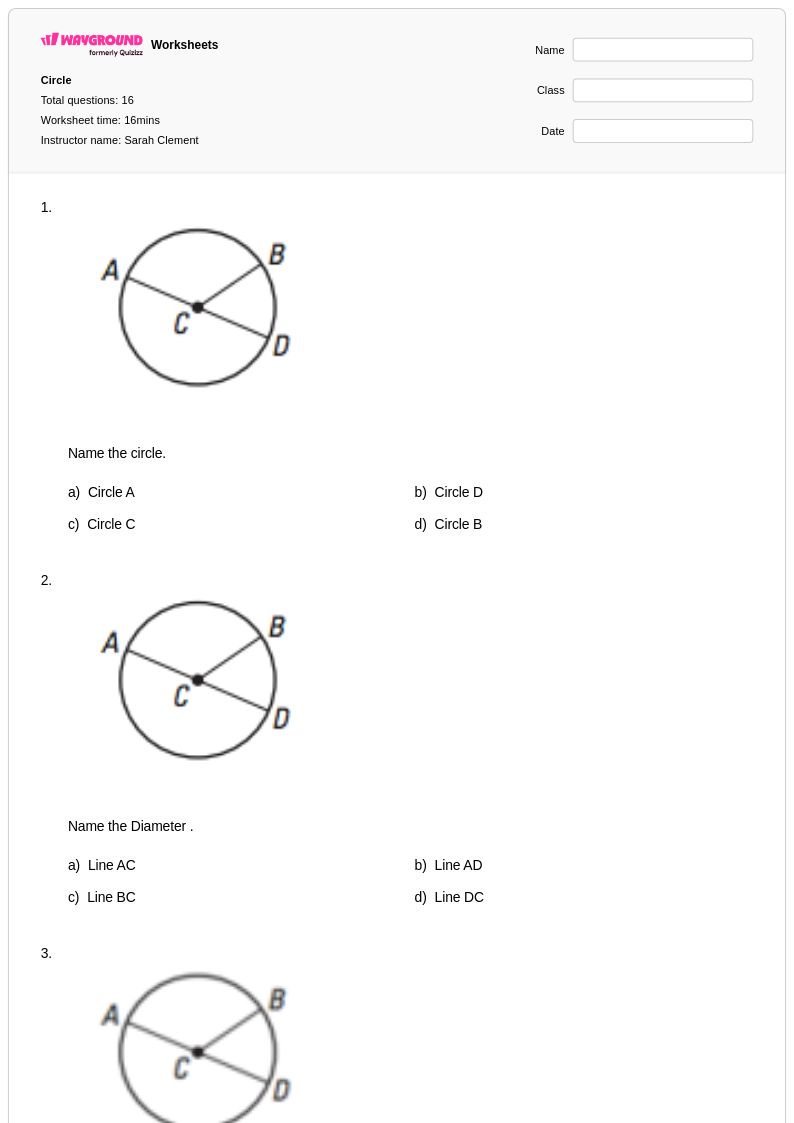
16 คิว
7th

17 คิว
7th
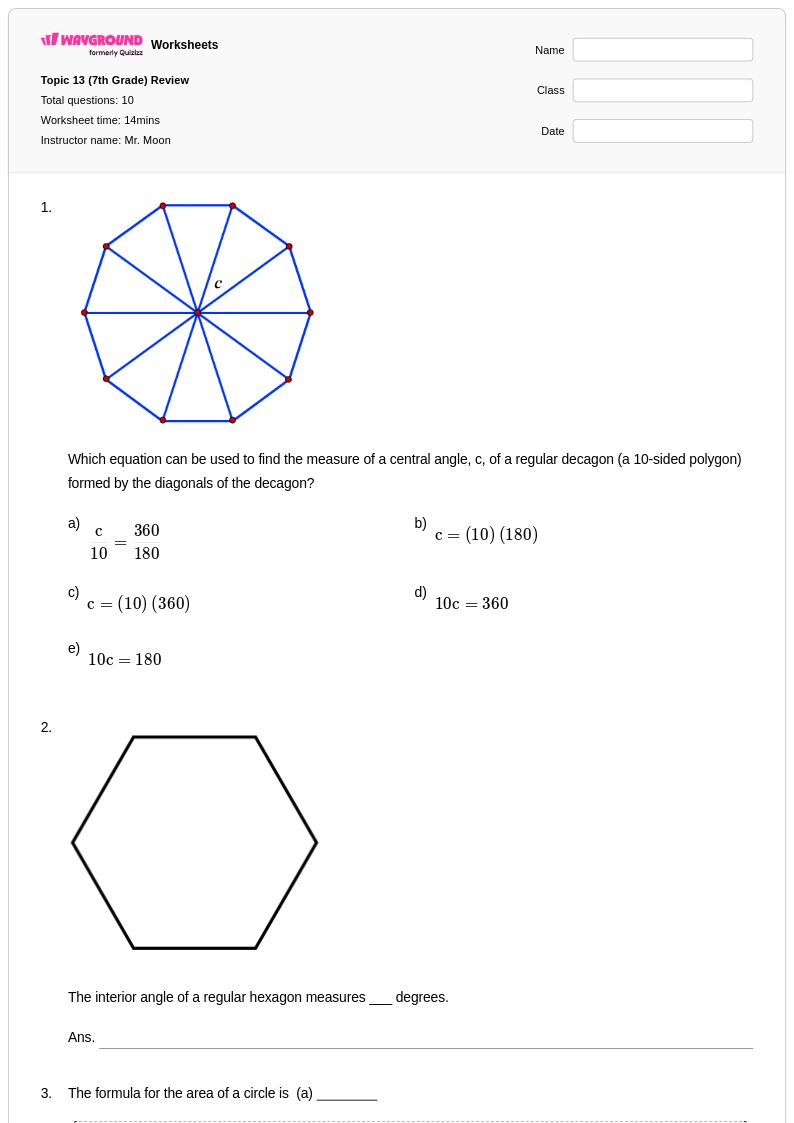
10 คิว
6th - 8th

20 คิว
6th - 8th
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน การพิสูจน์วงกลม ที่พิมพ์ได้
แบบฝึกหัดการพิสูจน์วงกลมที่มีให้ใช้งานผ่าน Wayground (เดิมคือ Quizizz) ช่วยให้นักเรียนคณิตศาสตร์ได้ฝึกฝนอย่างเป็นระบบในการสร้างข้อโต้แย้งเชิงตรรกะและตรวจสอบความสัมพันธ์ทางเรขาคณิตภายในรูปวงกลม แหล่งข้อมูลที่ครอบคลุมเหล่านี้ช่วยเสริมสร้างทักษะการคิดเชิงวิเคราะห์โดยนำนักเรียนผ่านกระบวนการที่เข้มงวดในการพิสูจน์ทฤษฎีบทที่เกี่ยวข้องกับคอร์ด เส้นสัมผัส เส้นตัด มุมภายในวงกลม และการวัดส่วนโค้ง แบบฝึกหัดแต่ละชุดประกอบด้วยโจทย์ฝึกหัดที่จัดเรียงอย่างระมัดระวังซึ่งพัฒนาจากแนวคิดพื้นฐานไปสู่การพิสูจน์หลายขั้นตอนที่ซับซ้อน พร้อมด้วยเฉลยที่แสดงให้เห็นถึงเหตุผลทางคณิตศาสตร์และรูปแบบที่ถูกต้อง นักเรียนพัฒนาความเชี่ยวชาญในการประยุกต์ใช้สัจพจน์และทฤษฎีบทที่ได้รับการยอมรับในขณะที่เรียนรู้ที่จะเขียนเหตุผลที่ชัดเจนและเป็นลำดับสำหรับข้อสรุปทางเรขาคณิตของพวกเขา เอกสารที่พิมพ์ได้ฟรีเหล่านี้เป็นเครื่องมือสำคัญในการเสริมสร้างการเรียนการสอนในห้องเรียนและสร้างความมั่นใจในการโต้แย้งทางคณิตศาสตร์อย่างเป็นทางการ
Wayground (เดิมคือ Quizizz) ช่วยเสริมศักยภาพครูคณิตศาสตร์ด้วยคลังข้อมูลขนาดใหญ่ที่มีทรัพยากรการพิสูจน์วงกลมที่สร้างโดยครูหลายล้านรายการ ซึ่งช่วยให้การวางแผนบทเรียนและการสอนที่แตกต่างกันมีประสิทธิภาพยิ่งขึ้น แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานและวัตถุประสงค์การเรียนรู้เฉพาะได้อย่างรวดเร็ว ในขณะที่เครื่องมือปรับแต่งในตัวช่วยให้สามารถปรับเปลี่ยนได้อย่างราบรื่นเพื่อตอบสนองความต้องการที่หลากหลายของนักเรียน ครูสามารถแจกจ่ายสื่อการเรียนการสอนได้อย่างมีประสิทธิภาพ ทั้งในรูปแบบไฟล์ PDF ที่พิมพ์ได้สำหรับการใช้งานในห้องเรียนแบบดั้งเดิม และรูปแบบดิจิทัลสำหรับสภาพแวดล้อมการเรียนรู้ที่บูรณาการเทคโนโลยี ทรัพยากรที่หลากหลายเหล่านี้สนับสนุนการแก้ไขปัญหาเฉพาะด้านสำหรับนักเรียนที่ประสบปัญหาเกี่ยวกับการให้เหตุผลทางเรขาคณิต มอบโอกาสในการเสริมสร้างความรู้สำหรับผู้เรียนขั้นสูงที่พร้อมสำหรับความท้าทายในการพิสูจน์ที่ซับซ้อน และเสนอการฝึกฝนทักษะอย่างสม่ำเสมอซึ่งเสริมสร้างโครงสร้างเชิงตรรกะที่จำเป็นสำหรับการเขียนพิสูจน์ทางคณิตศาสตร์
