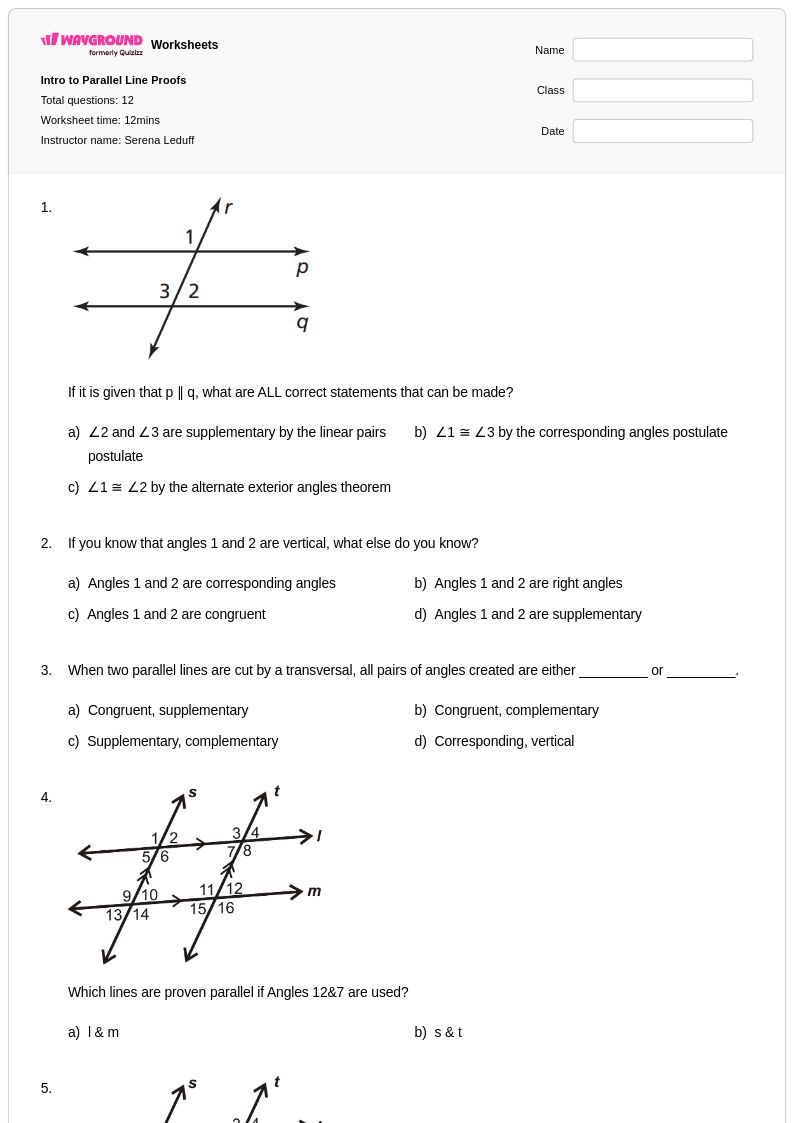
12 คิว
9th - 12th
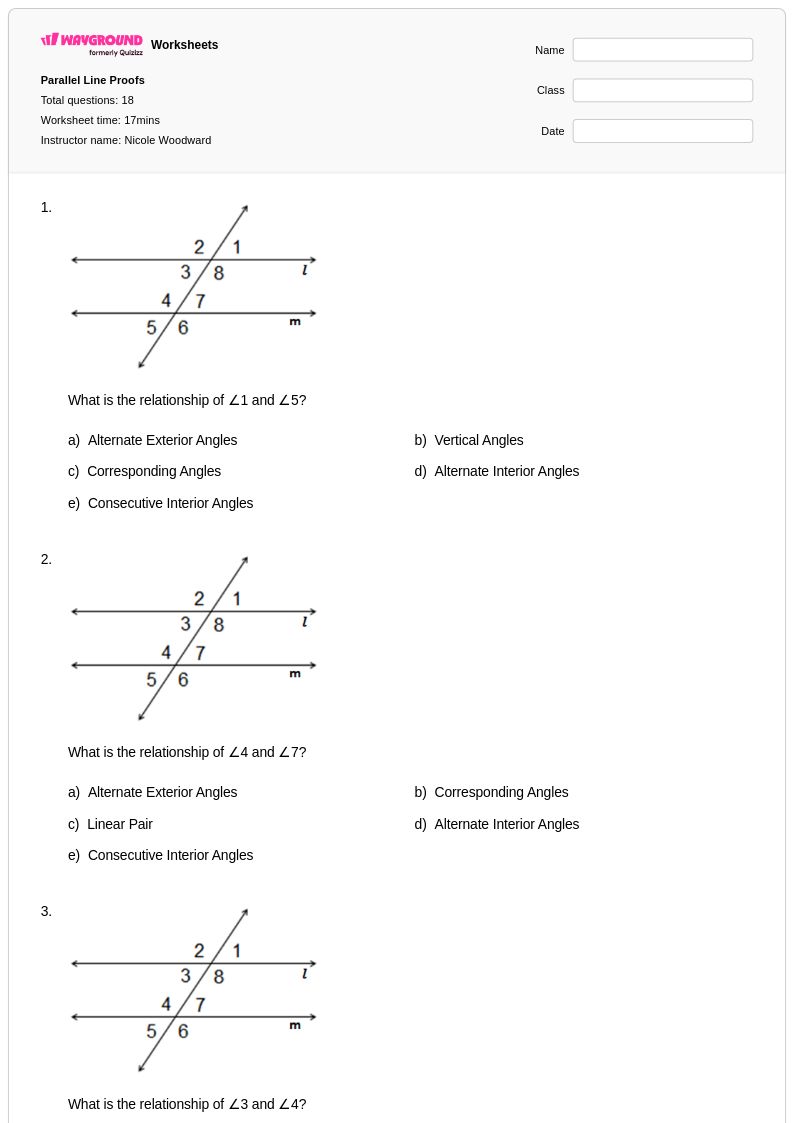
18 คิว
9th - 10th

20 คิว
9th - 12th

6 คิว
9th
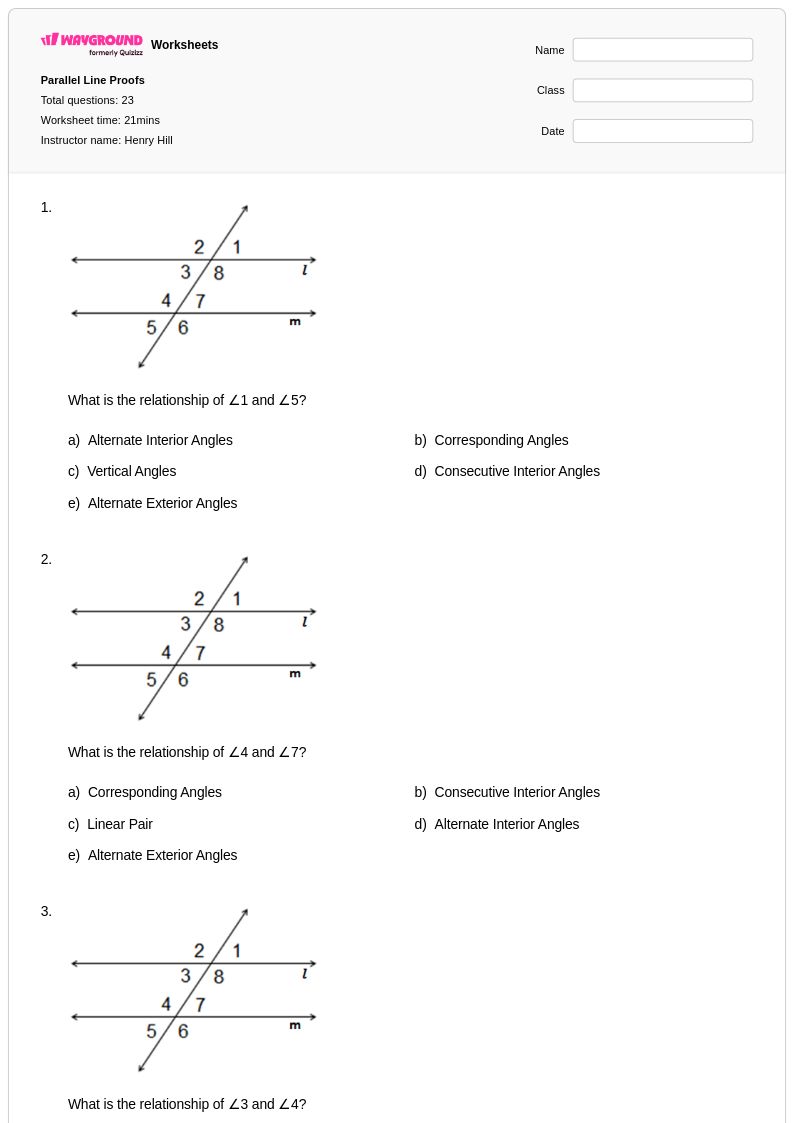
23 คิว
8th - 12th
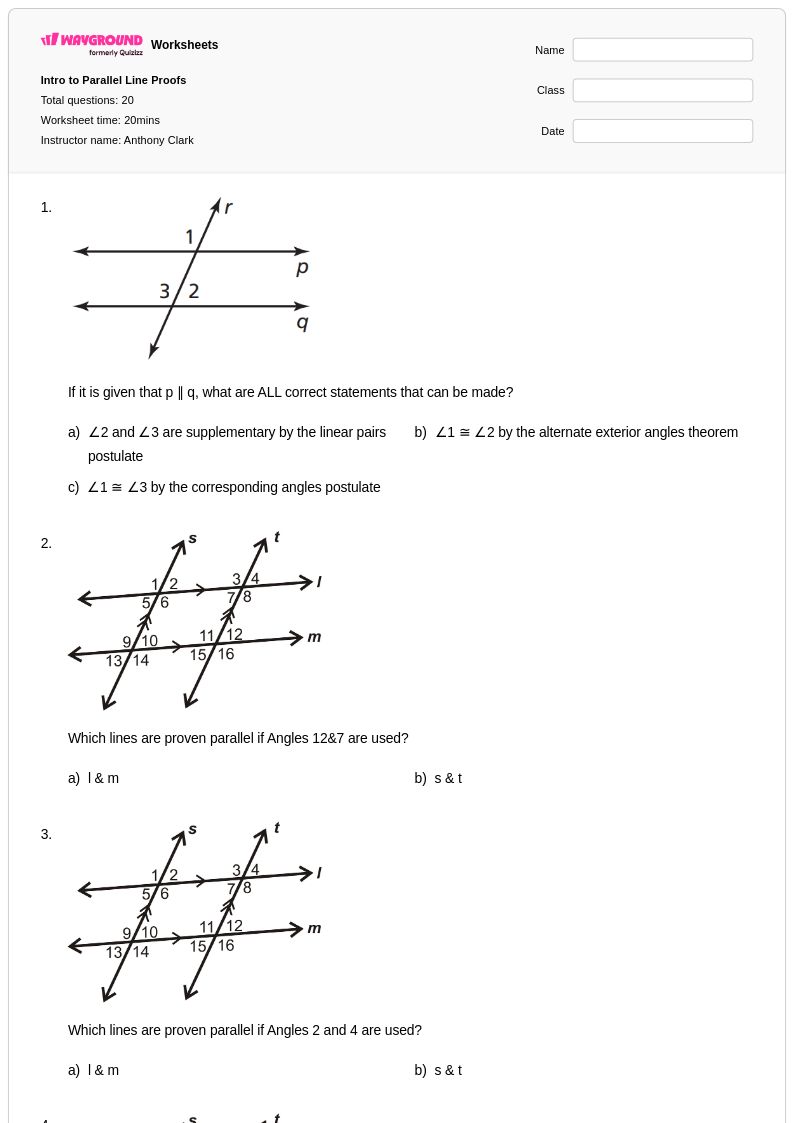
20 คิว
9th - Uni

16 คิว
9th - 12th

10 คิว
9th - 10th

13 คิว
9th

35 คิว
8th - 10th
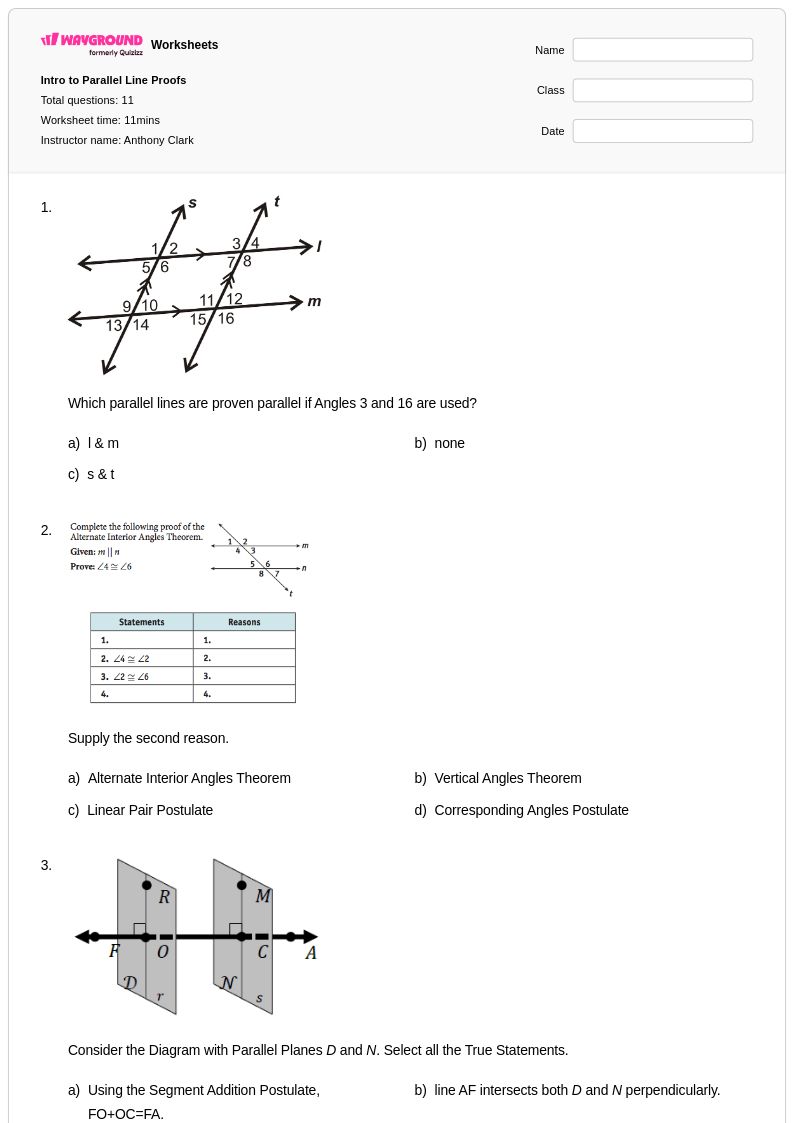
11 คิว
9th - Uni
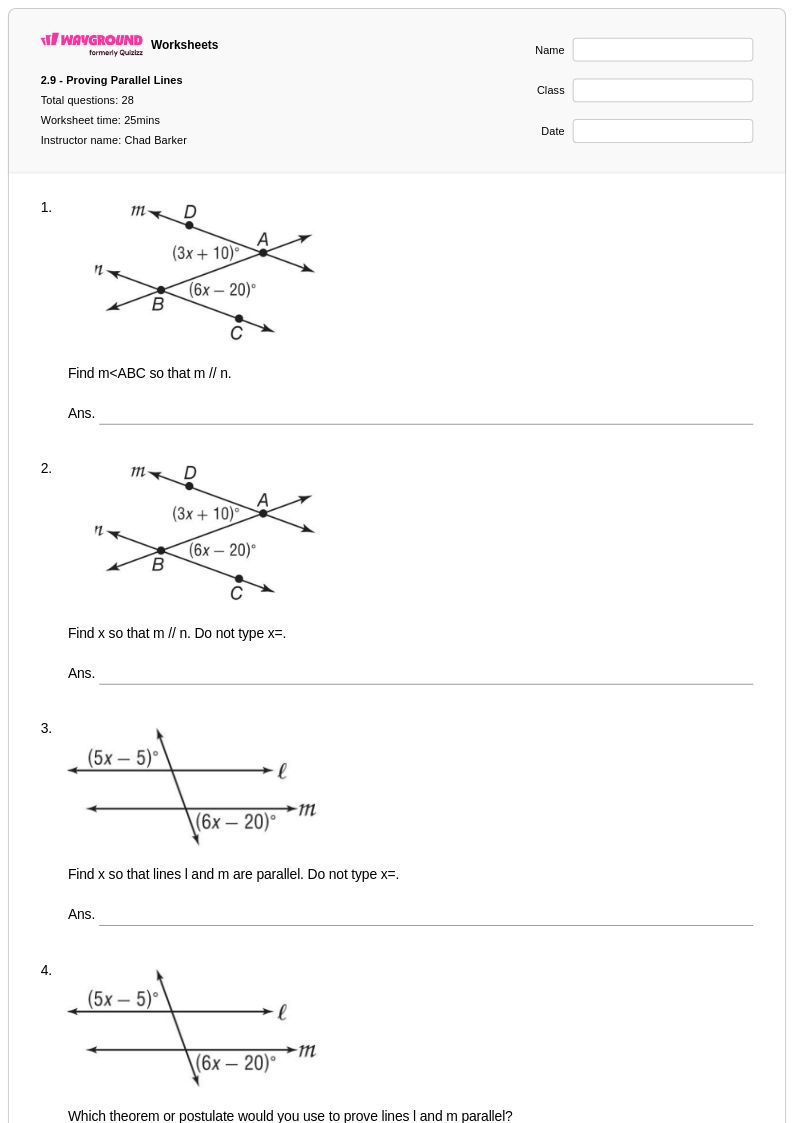
28 คิว
9th

29 คิว
8th - 11th
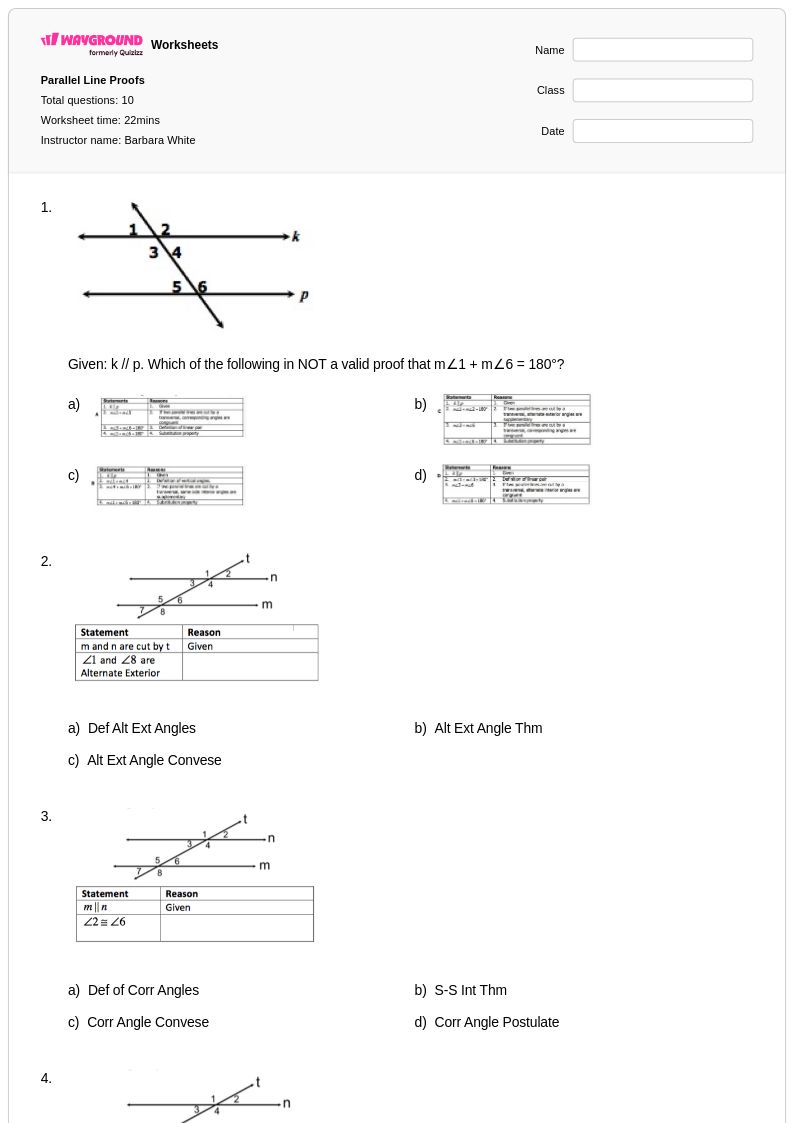
10 คิว
9th - 12th
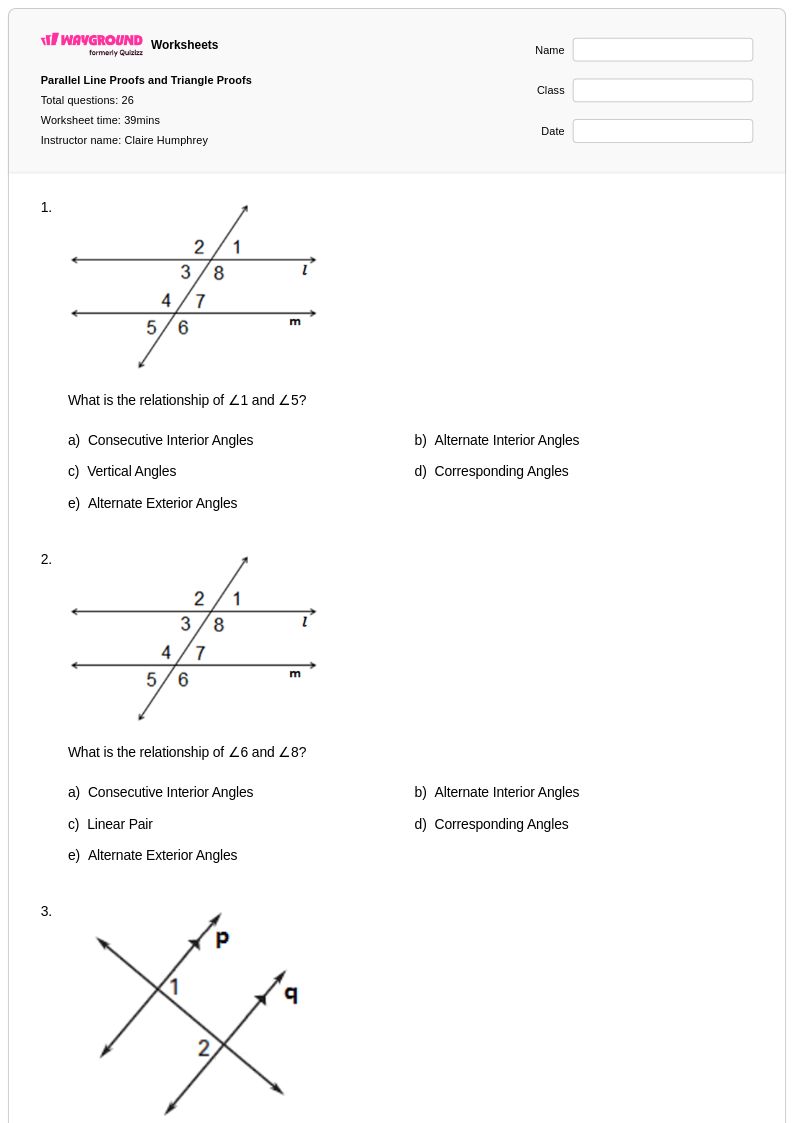
26 คิว
9th - 10th

18 คิว
9th - 12th

13 คิว
9th - 12th

60 คิว
8th - 11th

13 คิว
9th - 12th
10 คิว
8th - 10th
12 คิว
9th

12 คิว
9th

40 คิว
9th - 12th

10 คิว
9th - 12th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 9
สำรวจแผ่นงาน การพิสูจน์เส้นขนาน ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 9
การพิสูจน์เส้นขนานสำหรับนักเรียนชั้นมัธยมศึกษาปีที่ 3 (เกรด 3) เป็นพื้นฐานสำคัญของการให้เหตุผลทางเรขาคณิต ซึ่งต้องอาศัยความเข้าใจโครงสร้างเชิงตรรกะของการให้เหตุผลทางคณิตศาสตร์ พร้อมทั้งการประยุกต์ใช้ทฤษฎีบทสำคัญเกี่ยวกับเส้นขนานที่ถูกตัดด้วยเส้นตัดขวาง ชุดแบบฝึกหัดการพิสูจน์เส้นขนานที่ครอบคลุมของ Wayground ช่วยให้ฝึกฝนความสัมพันธ์ของมุมอย่างเป็นระบบ รวมถึงมุมที่สมนัยกัน มุมภายในสลับ มุมภายนอกสลับ และมุมภายในด้านเดียวกัน แบบฝึกหัดที่ออกแบบมาอย่างพิถีพิถันเหล่านี้จะแนะนำนักเรียนทีละขั้นตอนในการสร้างการพิสูจน์ทางเรขาคณิตอย่างเป็นทางการ เสริมสร้างความสามารถในการระบุข้อมูลที่กำหนด ประยุกต์ใช้ทฤษฎีบทที่เกี่ยวข้อง และเขียนลำดับตรรกะของข้อความและเหตุผล แบบฝึกหัดแต่ละชุดมีเฉลยโดยละเอียดที่แสดงรูปแบบการพิสูจน์และสัญลักษณ์ทางคณิตศาสตร์ที่ถูกต้อง ในขณะที่รูปแบบ PDF ที่พิมพ์ได้ฟรีช่วยให้แจกจ่ายในห้องเรียนและมอบหมายการบ้านได้ง่าย
Wayground ซึ่งเดิมชื่อ Quizizz ช่วยเสริมศักยภาพครูคณิตศาสตร์ด้วยแหล่งข้อมูลนับล้านที่สร้างโดยครูโดยเฉพาะ ซึ่งมุ่งเน้นไปที่การพิสูจน์เส้นขนานและแนวคิดการให้เหตุผลทางเรขาคณิต ความสามารถในการค้นหาและกรองขั้นสูงของแพลตฟอร์มช่วยให้ครูผู้สอนสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานหลักสูตรเฉพาะได้อย่างรวดเร็ว และปรับการสอนให้เหมาะสมกับความต้องการของนักเรียนแต่ละคน ครูสามารถปรับแต่งแบบฝึกหัดการพิสูจน์เส้นขนานที่มีอยู่แล้ว หรือสร้างเนื้อหาใหม่โดยใช้เครื่องมือดิจิทัลที่ยืดหยุ่น จากนั้นเผยแพร่สื่อได้อย่างราบรื่นทั้งในรูปแบบสิ่งพิมพ์และรูปแบบดิจิทัลแบบโต้ตอบ ชุดทรัพยากรที่ครอบคลุมนี้สนับสนุนเป้าหมายการสอนที่หลากหลาย รวมถึงการแนะนำแนวคิดเบื้องต้น การแก้ไขทักษะเฉพาะสำหรับนักเรียนที่ประสบปัญหา และกิจกรรมเสริมสำหรับผู้เรียนที่มีความสามารถสูง ช่วยให้ครูสามารถให้การฝึกฝนที่สอดคล้องกับมาตรฐานและสร้างความมั่นใจให้กับนักเรียนในการสร้างการพิสูจน์ทางเรขาคณิต
