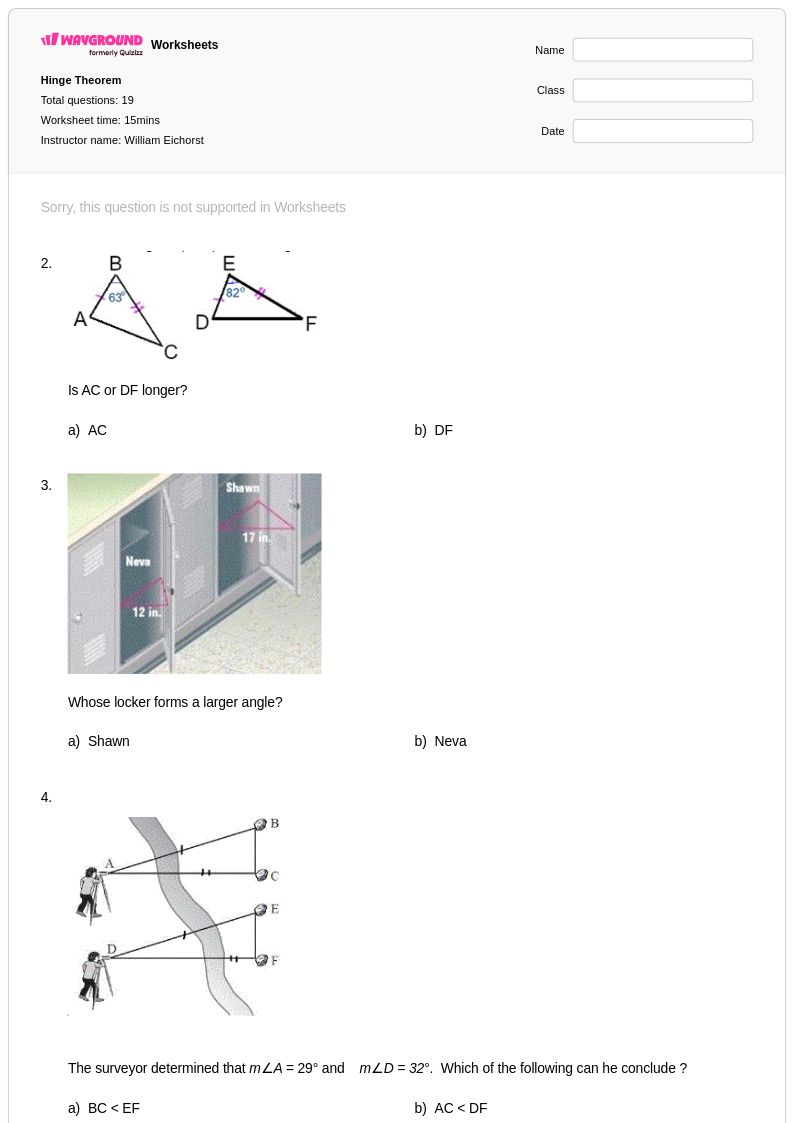
21 คิว
9th - 12th
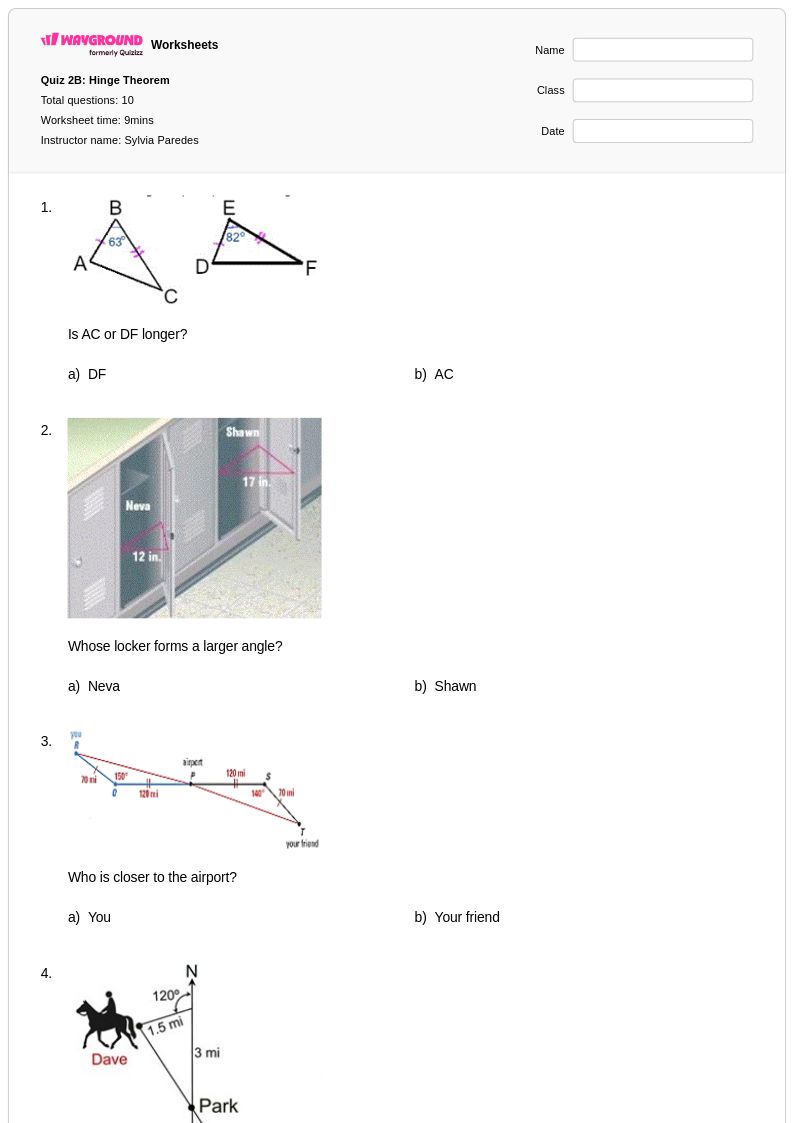
10 คิว
9th - 12th

15 คิว
9th - 12th
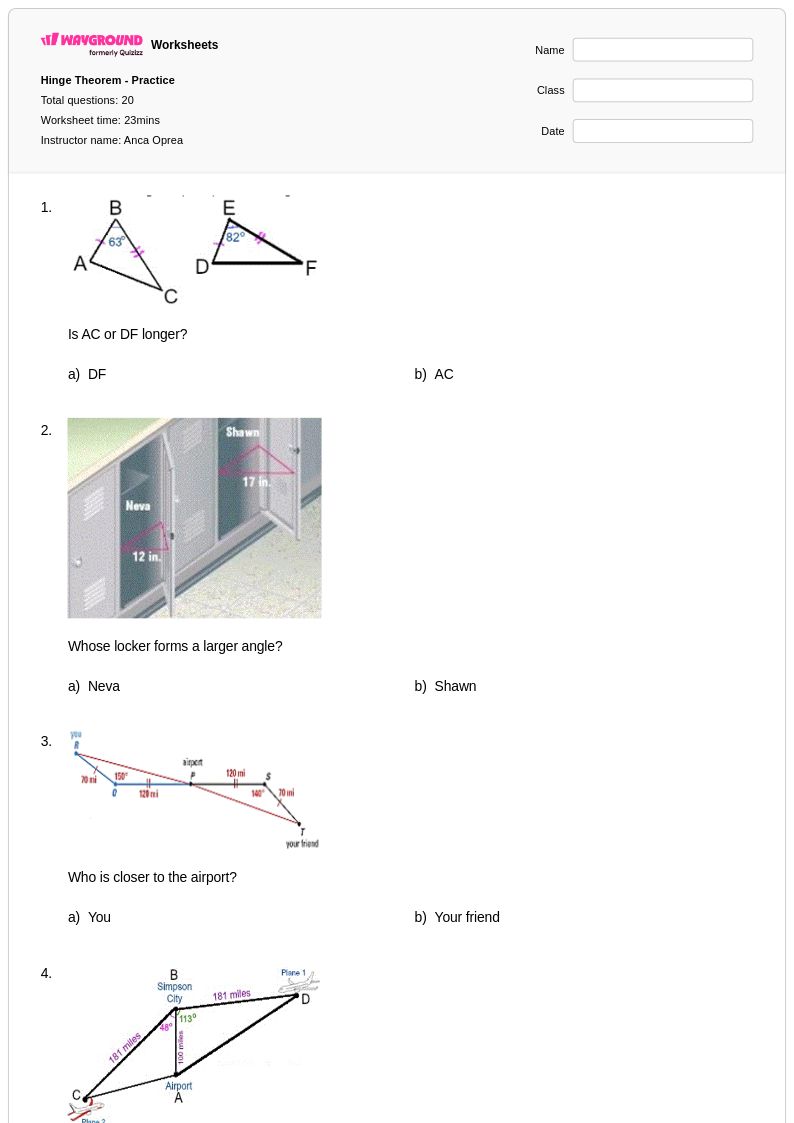
20 คิว
9th - 12th
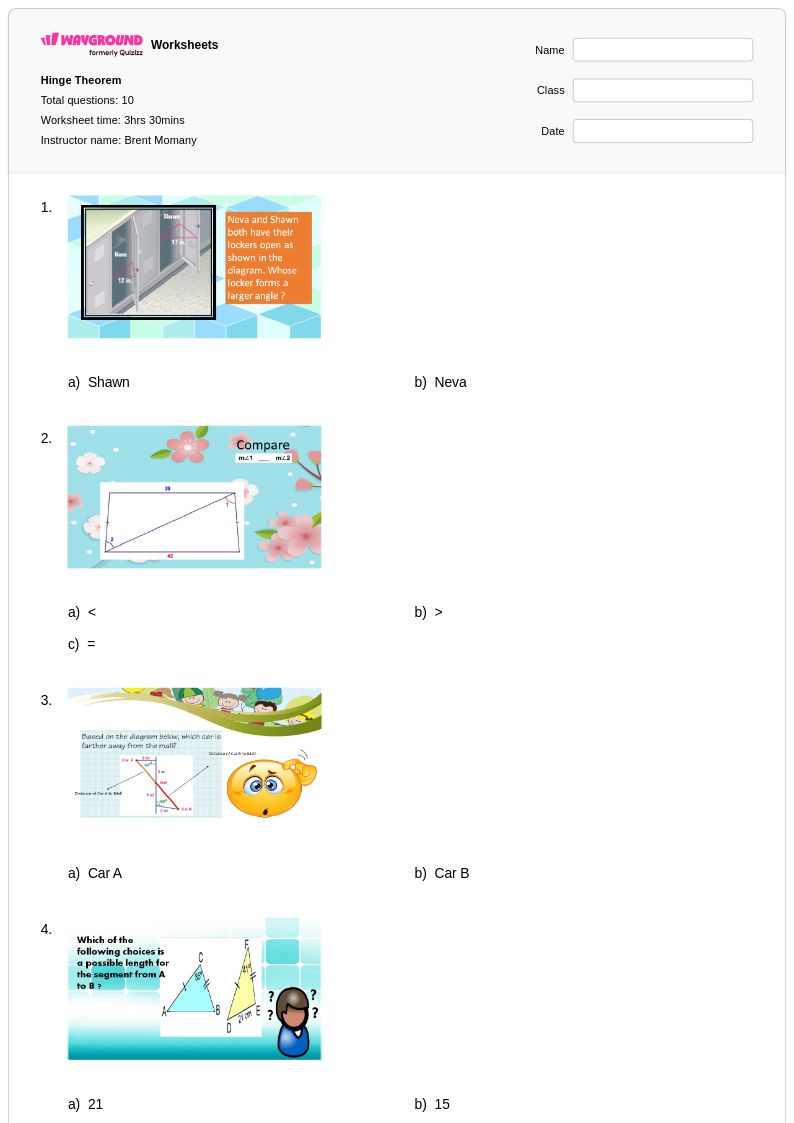
10 คิว
9th
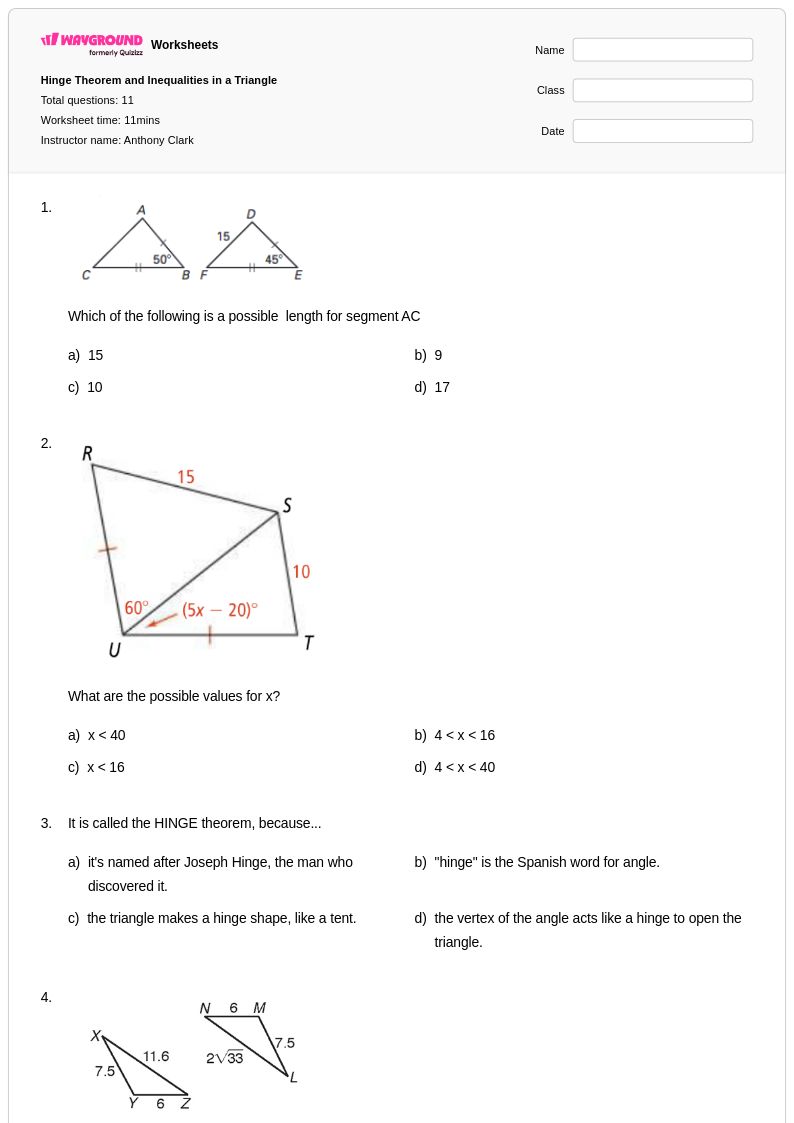
11 คิว
8th - Uni
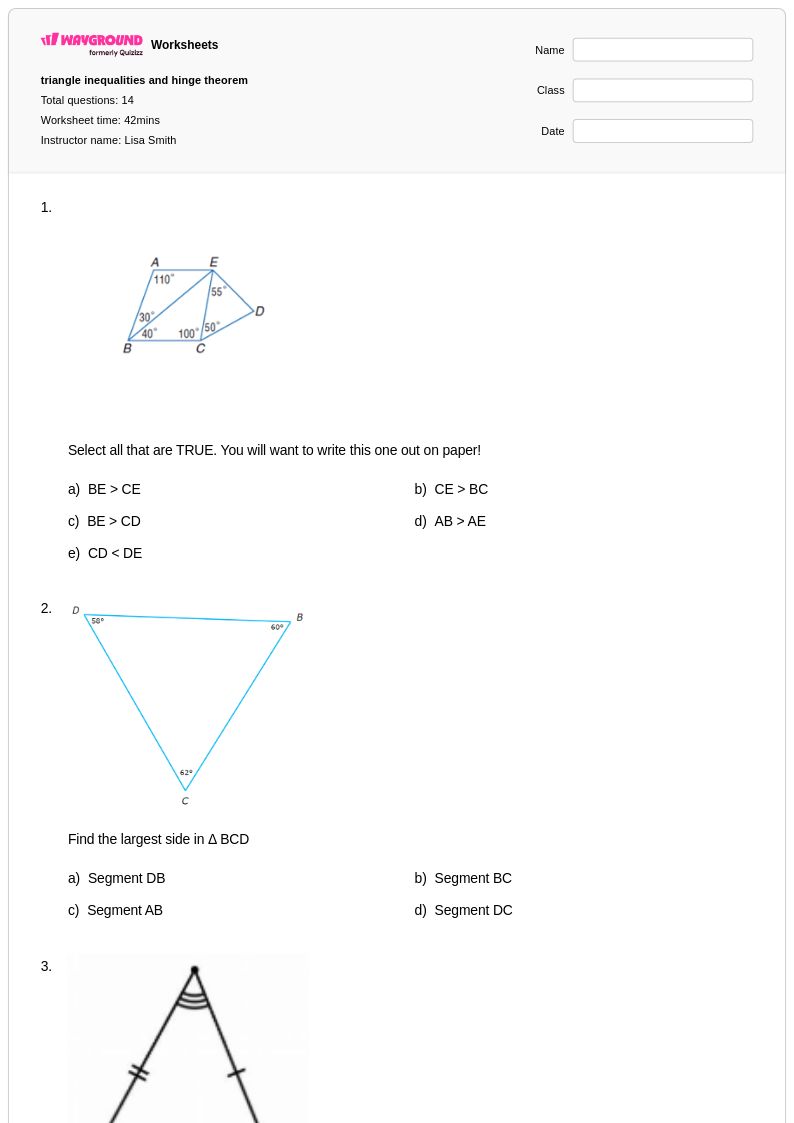
14 คิว
9th - 12th
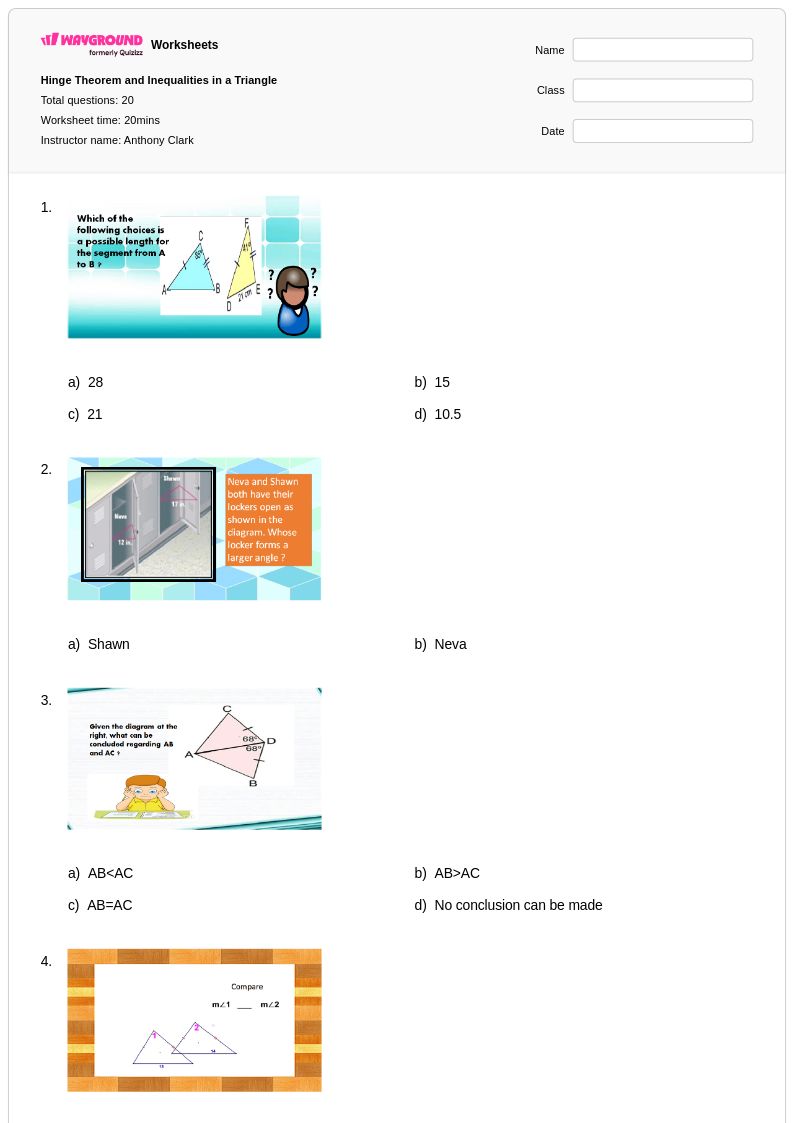
20 คิว
8th - Uni
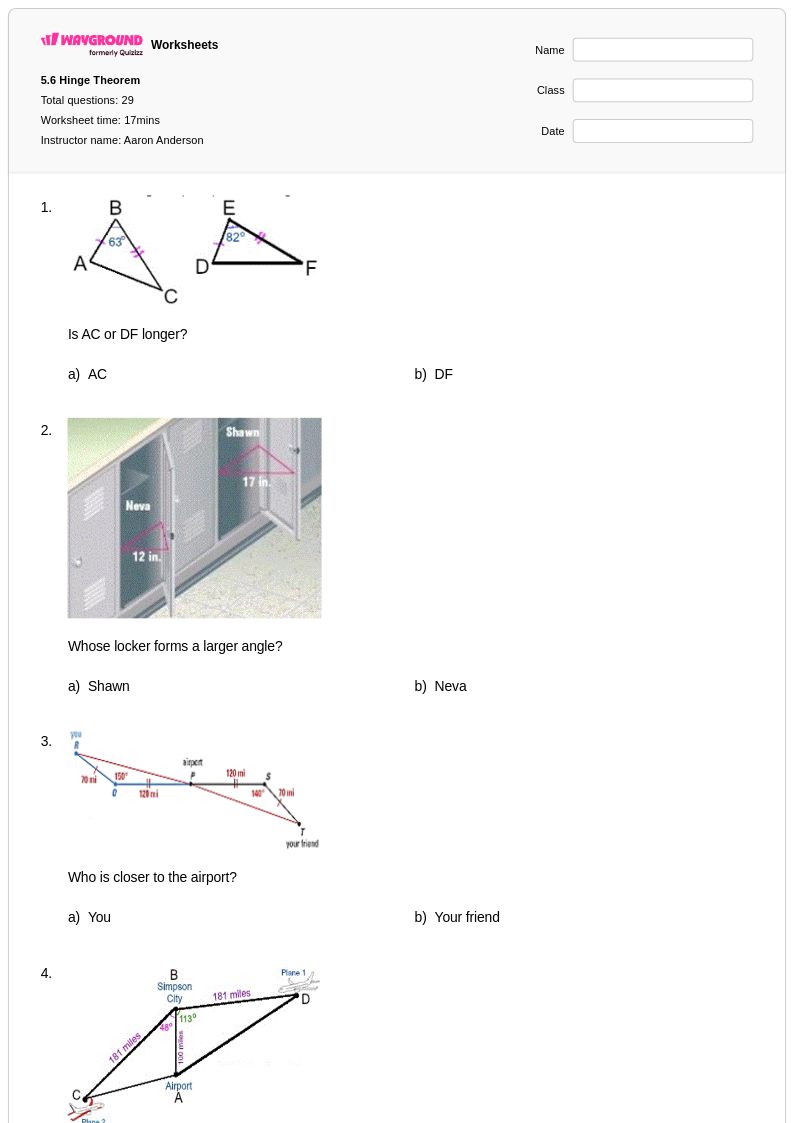
29 คิว
9th
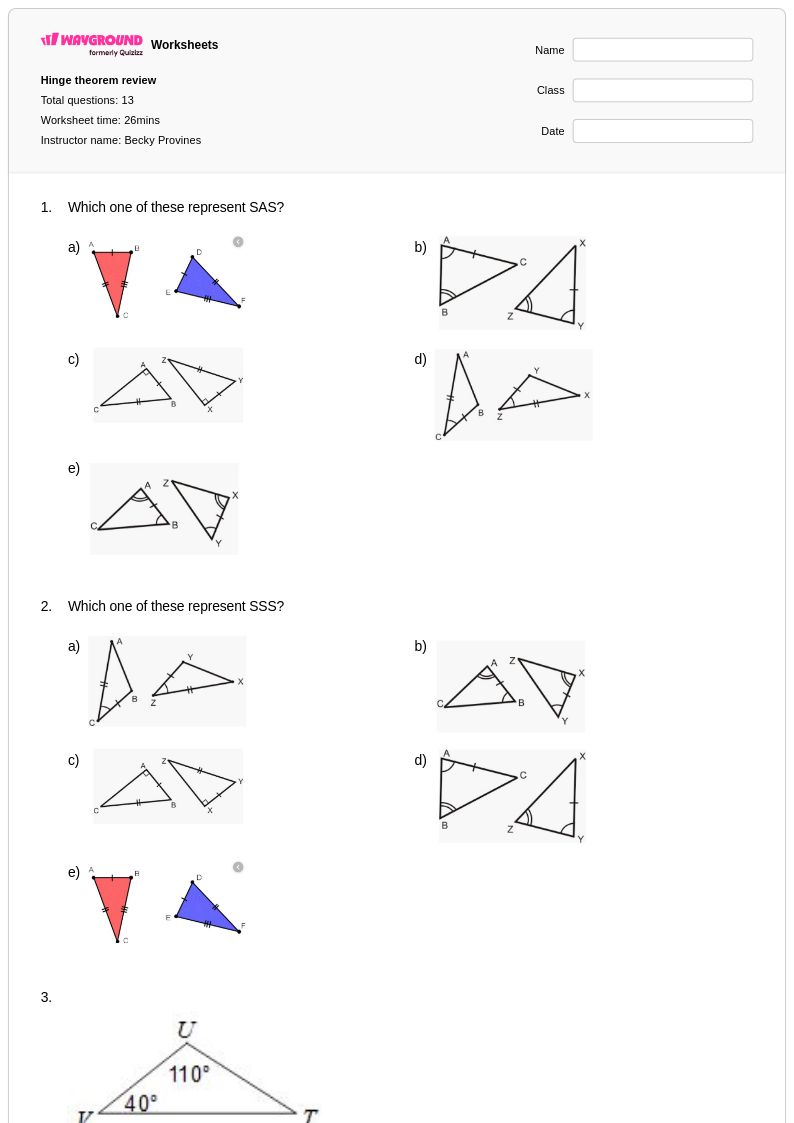
13 คิว
9th
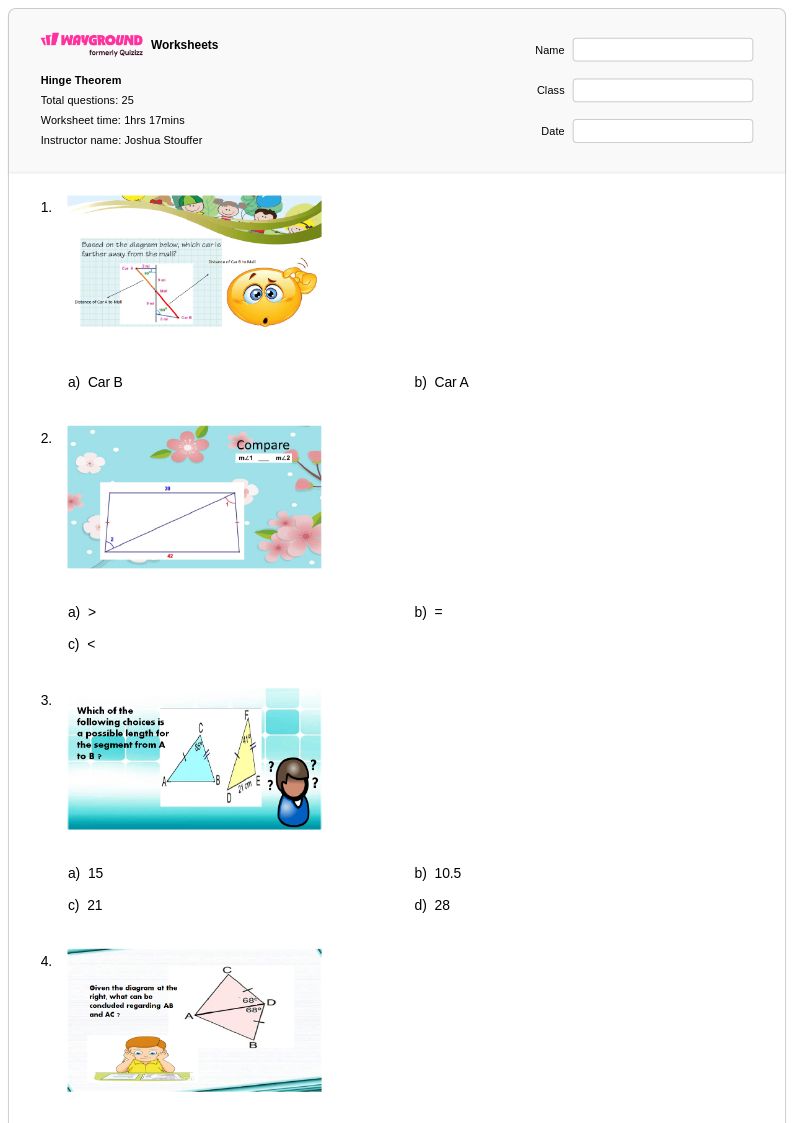
25 คิว
9th - 12th
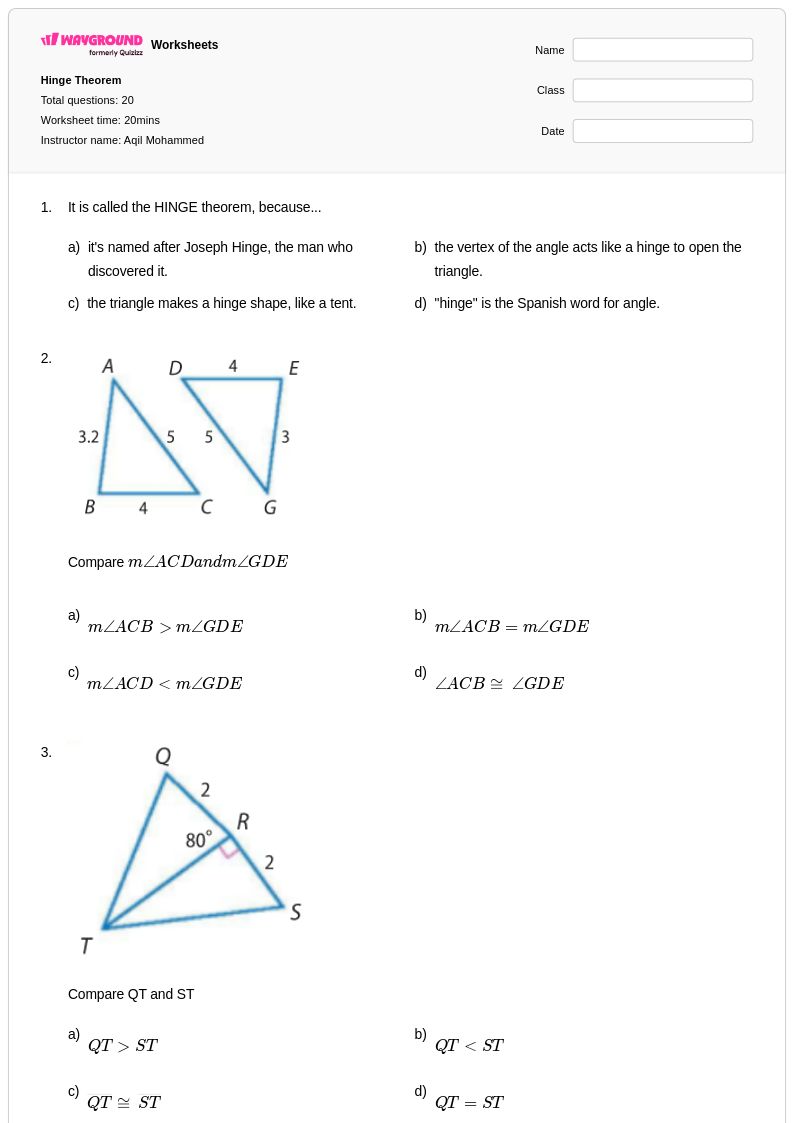
20 คิว
8th - 10th
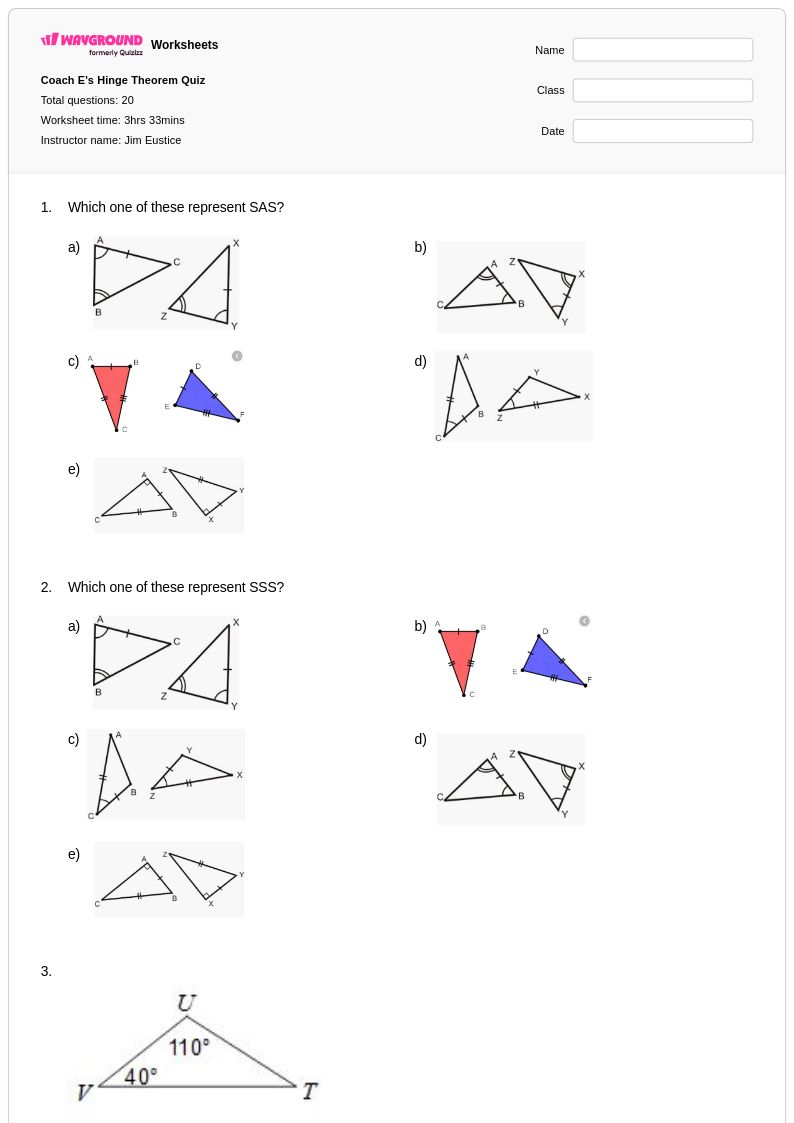
20 คิว
9th - 10th
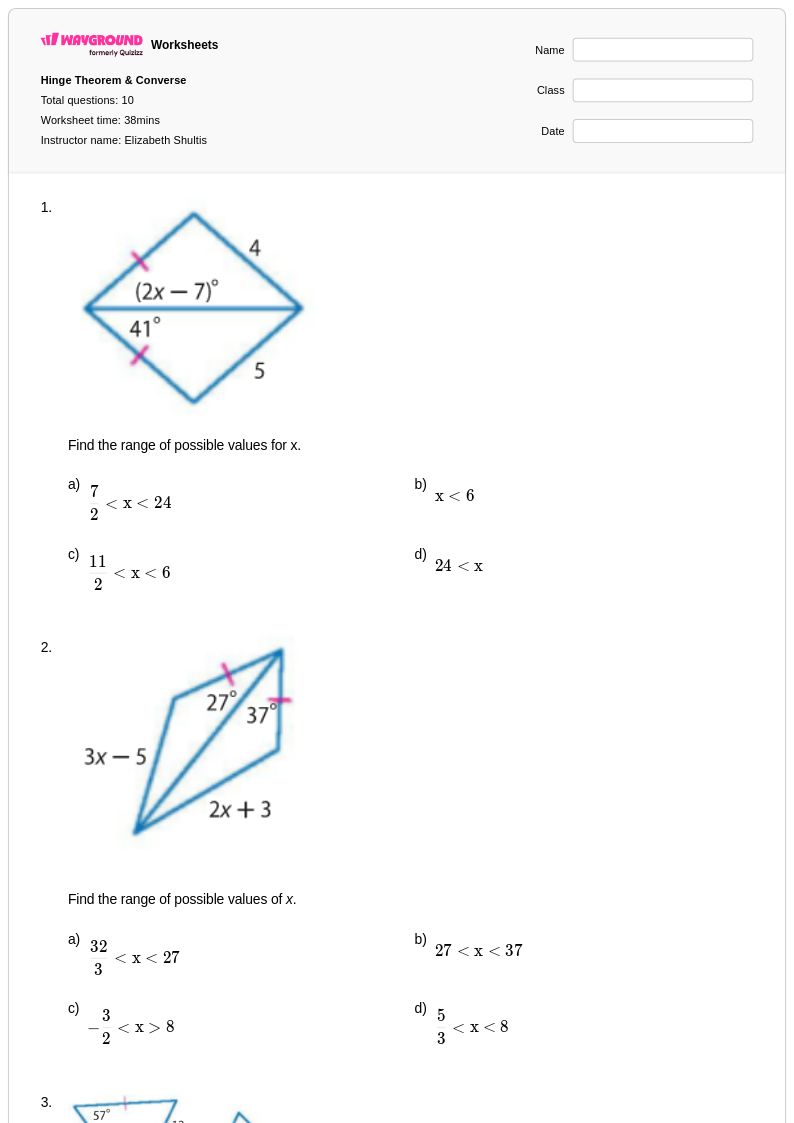
10 คิว
9th - 12th
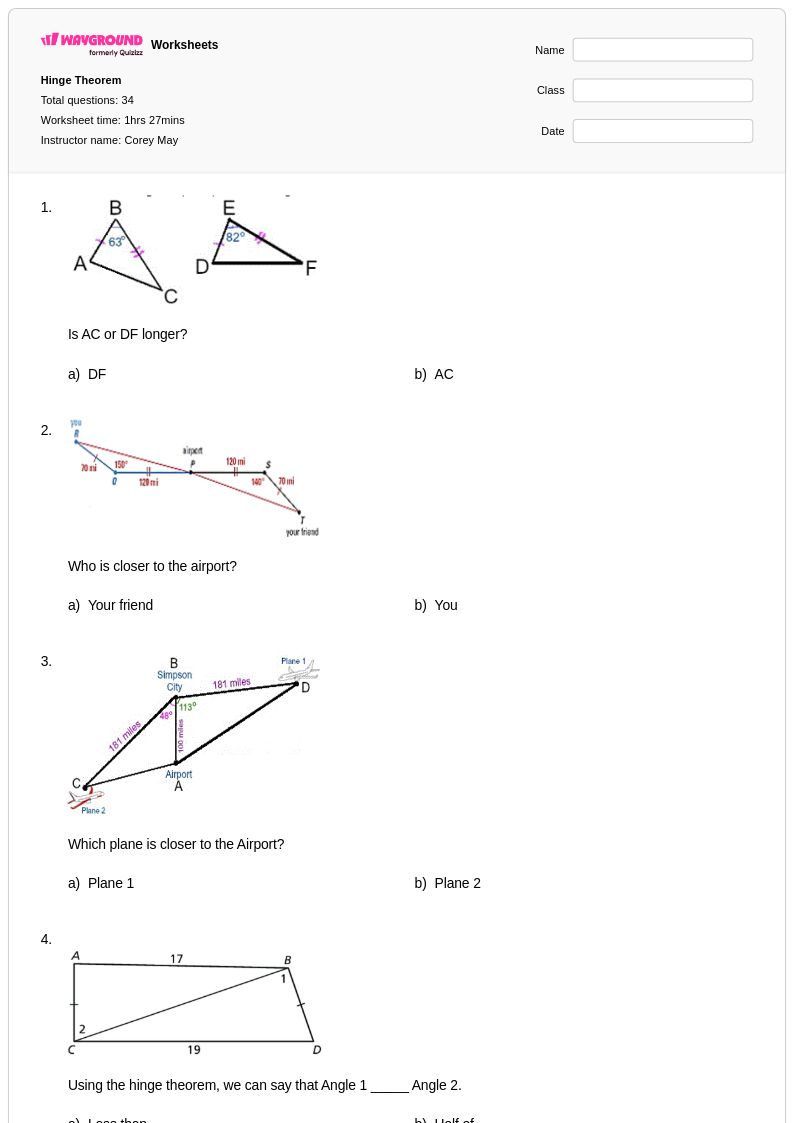
34 คิว
9th - 12th

28 คิว
8th - 12th
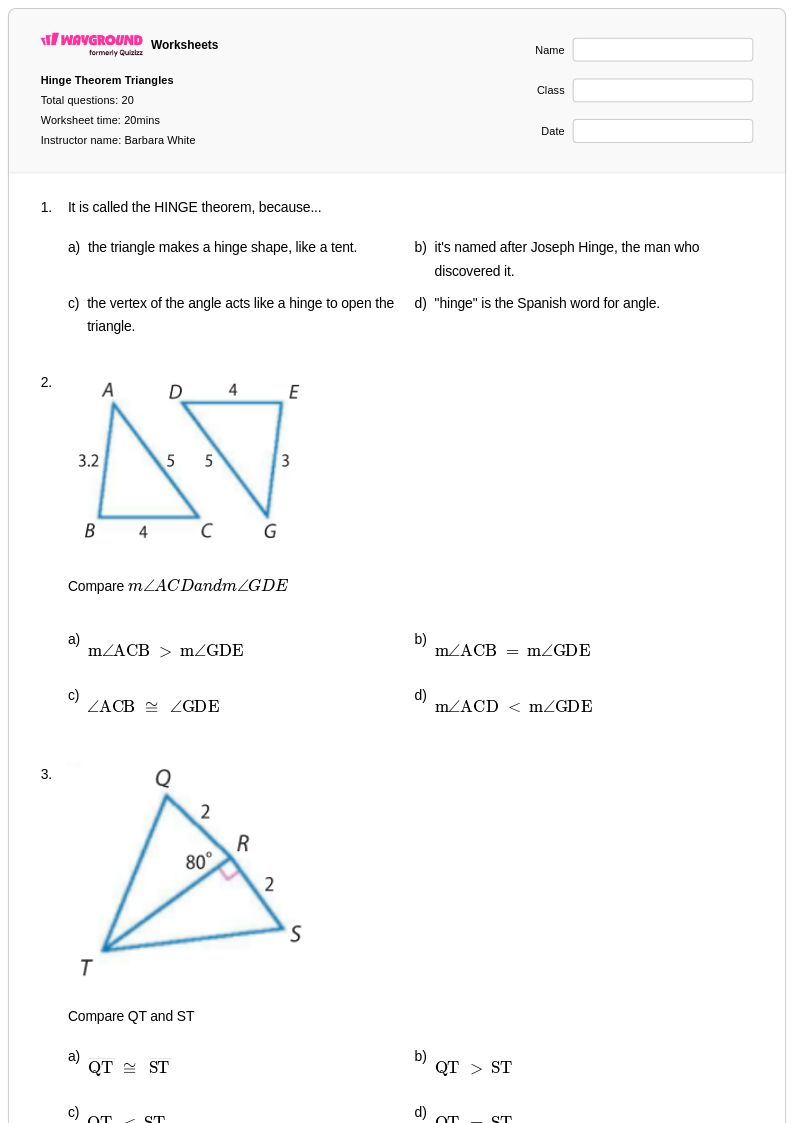
20 คิว
8th - 10th
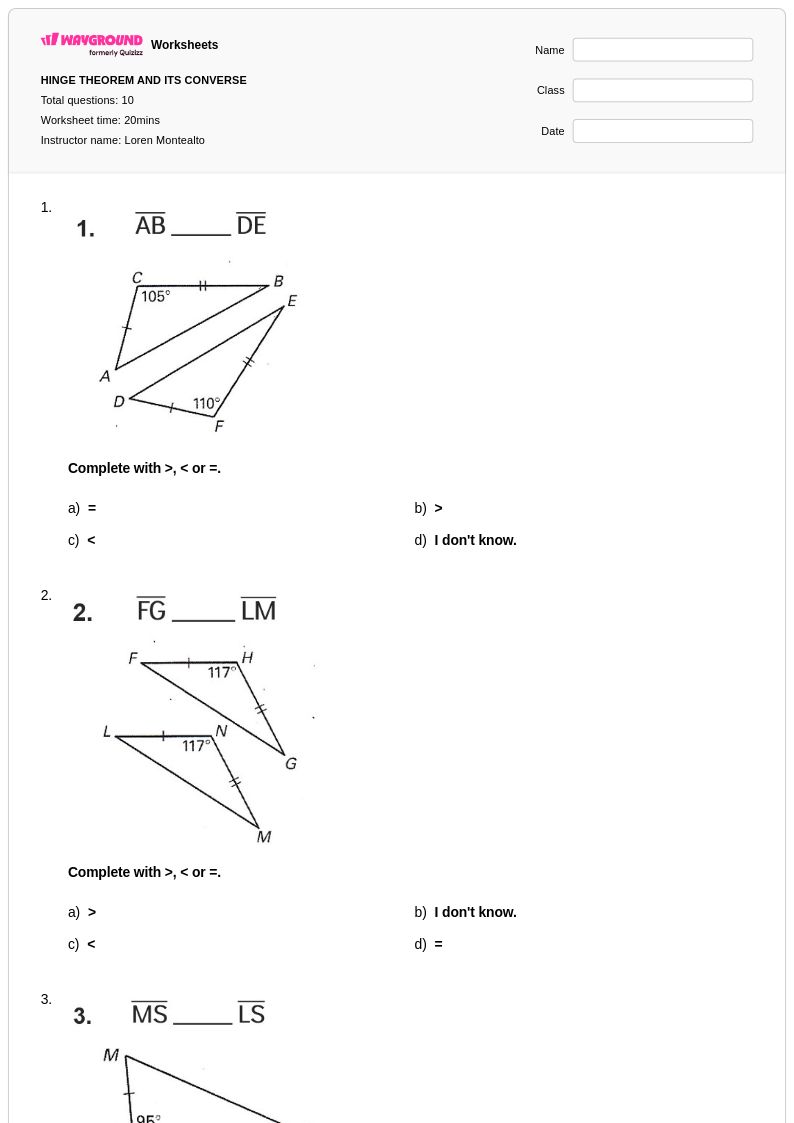
10 คิว
8th - 12th

14 คิว
9th

5 คิว
6th - 10th

17 คิว
9th - 12th
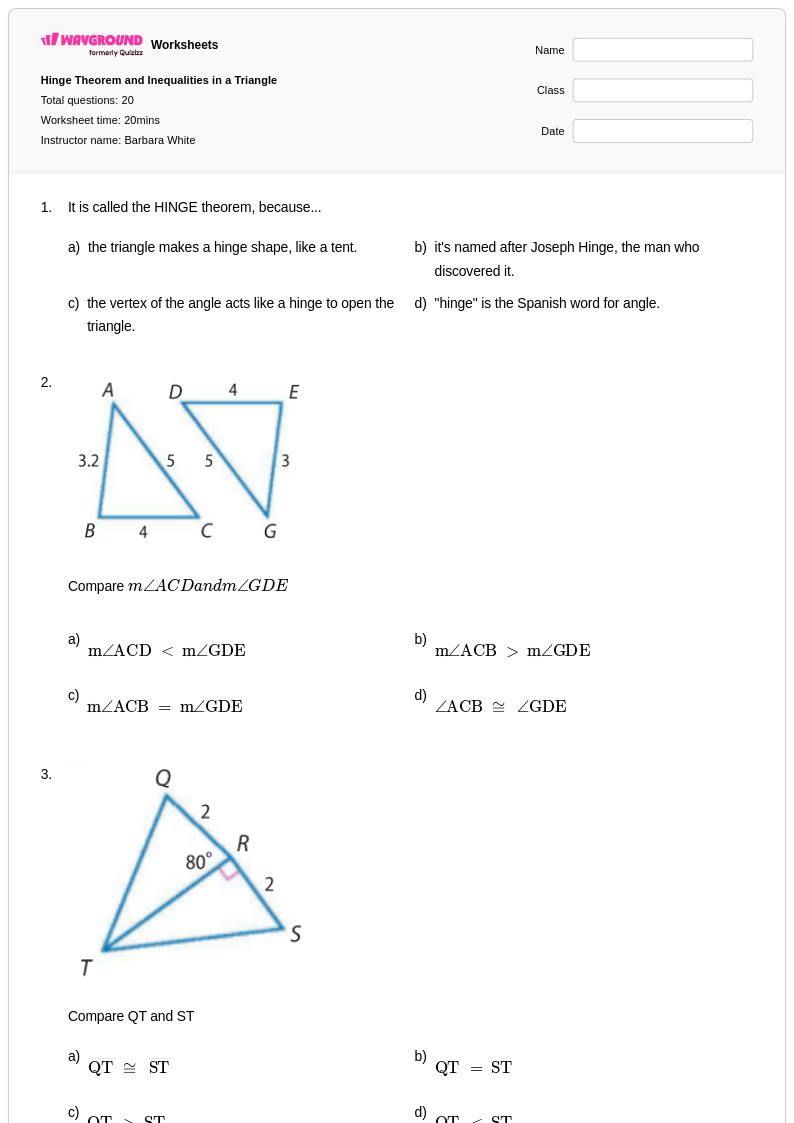
20 คิว
8th - 10th
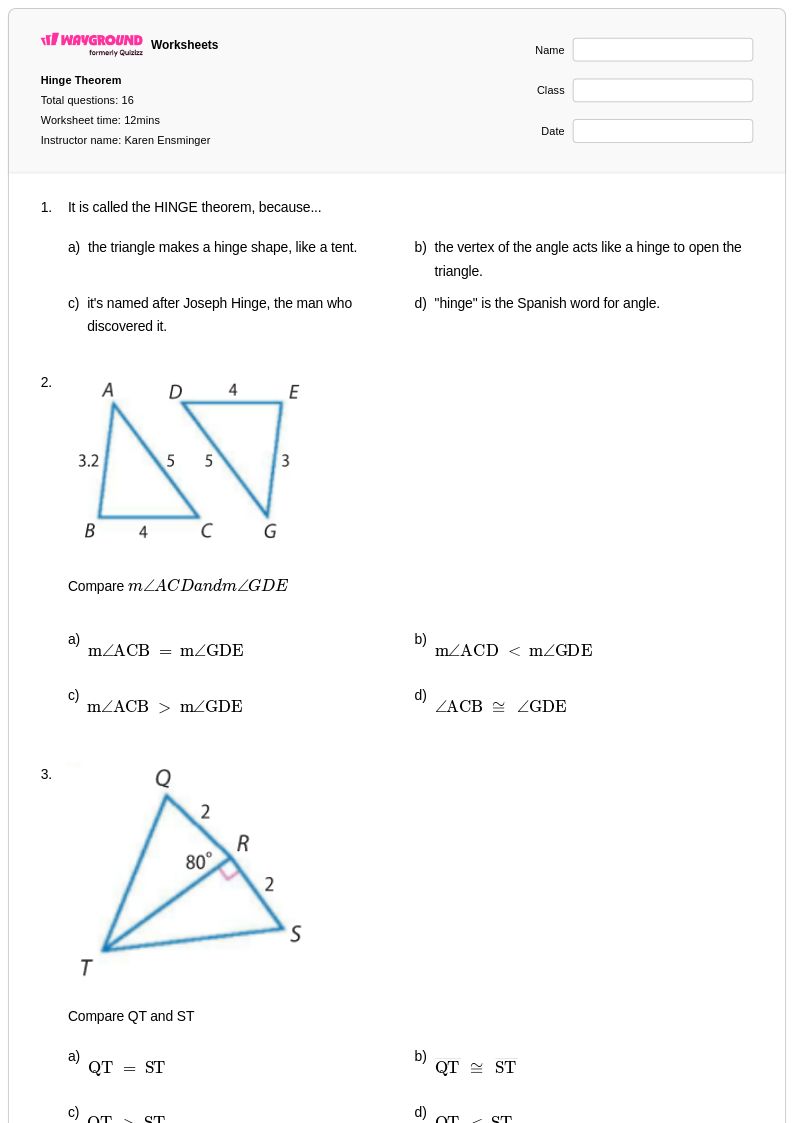
16 คิว
9th
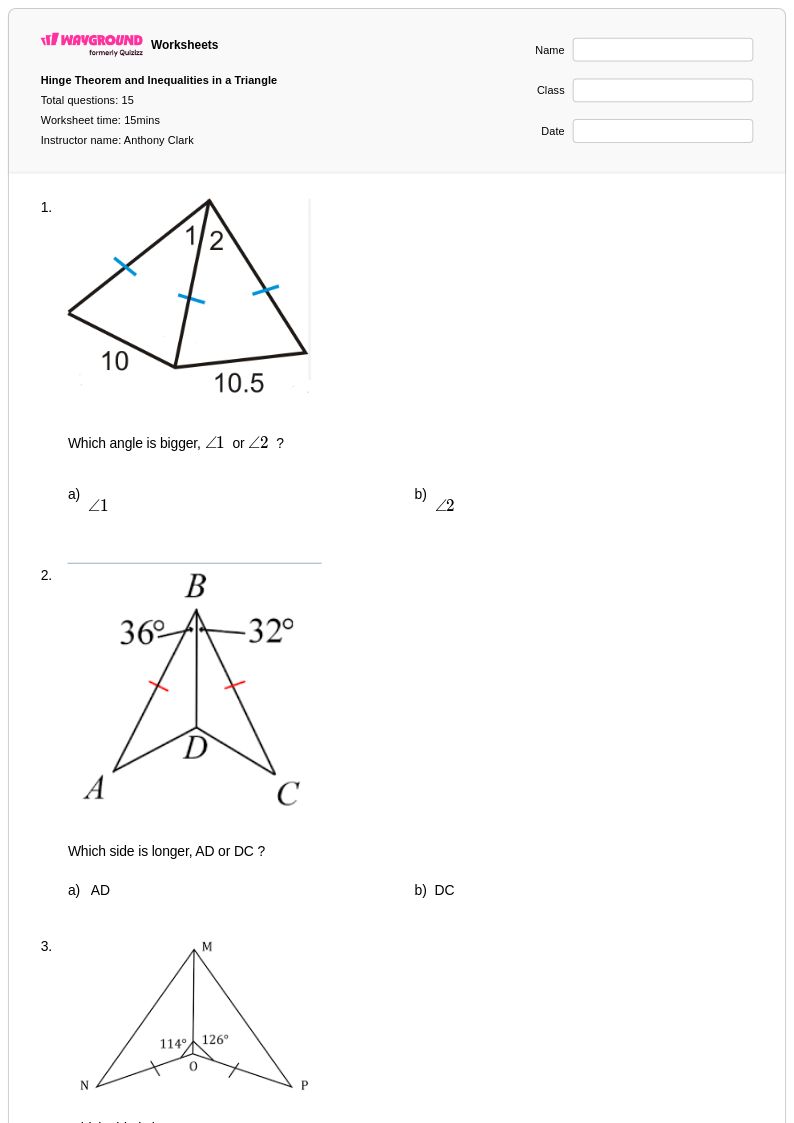
15 คิว
8th - Uni
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 9
สำรวจแผ่นงาน ทฤษฎีบทบานพับ ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 9
แบบฝึกหัดทฤษฎีบทบานพับสำหรับนักเรียนชั้นมัธยมศึกษาปีที่ 3 จาก Wayground ให้แบบฝึกหัดที่ครอบคลุมเกี่ยวกับหลักการทางเรขาคณิตพื้นฐานนี้ ซึ่งเชื่อมโยงความยาวด้านกับขนาดมุมในรูปสามเหลี่ยม แหล่งข้อมูลที่ออกแบบมาอย่างเชี่ยวชาญเหล่านี้ช่วยให้นักเรียนเข้าใจแนวคิดที่ว่า เมื่อด้านสองด้านของรูปสามเหลี่ยมหนึ่งเท่ากันกับด้านสองด้านของรูปสามเหลี่ยมอีกรูปหนึ่ง รูปสามเหลี่ยมที่มีมุมระหว่างด้านใหญ่กว่าจะมีด้านที่สามยาวกว่า และในทางกลับกัน รูปสามเหลี่ยมที่มีด้านที่สามยาวกว่าจะมีมุมระหว่างด้านใหญ่กว่า แบบฝึกหัดเหล่านี้เสริมสร้างทักษะการคิดเชิงวิเคราะห์ผ่านแบบฝึกหัดที่เป็นระบบซึ่งต้องการให้นักเรียนเปรียบเทียบรูปสามเหลี่ยม วิเคราะห์ข้อมูลที่กำหนด และใช้เหตุผลเชิงตรรกะเพื่อกำหนดความสัมพันธ์ระหว่างมุมและด้าน แบบฝึกหัดแต่ละชุดมีเฉลยครบถ้วนและมีให้ดาวน์โหลดเป็นไฟล์ PDF ที่พิมพ์ได้ฟรี ทำให้ครูผู้สอนสามารถนำข้อเสนอแนะและการประเมินผลไปใช้ในการสอนเรขาคณิตได้อย่างง่ายดาย
Wayground สนับสนุนครูผู้สอนคณิตศาสตร์ด้วยชุดทรัพยากรทฤษฎีบทบานพับที่สร้างโดยครูผู้สอนจำนวนมาก ซึ่งสามารถค้นหาได้ง่ายผ่านความสามารถในการค้นหาและกรองข้อมูลที่มีประสิทธิภาพซึ่งออกแบบมาโดยเฉพาะสำหรับเนื้อหาทางการศึกษา แบบฝึกหัดนับล้านชุดในแพลตฟอร์มนี้สอดคล้องกับมาตรฐานหลักสูตร และมีเครื่องมือช่วยปรับระดับความยากง่ายที่ช่วยให้ครูสามารถปรับแต่งสื่อการเรียนการสอนให้เหมาะสมกับระดับความสามารถของนักเรียนที่แตกต่างกัน ตั้งแต่การแนะนำแนวคิดพื้นฐานไปจนถึงการประยุกต์ใช้การเขียนพิสูจน์ขั้นสูง ครูสามารถเข้าถึงแหล่งข้อมูลเหล่านี้ได้ทั้งในรูปแบบไฟล์ PDF ที่พิมพ์ได้และเวอร์ชันดิจิทัลแบบโต้ตอบ ซึ่งให้ความยืดหยุ่นสำหรับการสอนในห้องเรียน การบ้าน และการเรียนรู้ด้วยตนเอง แนวทางที่ครอบคลุมนี้ช่วยให้ครูสามารถวางแผนบทเรียนได้อย่างมีประสิทธิภาพ ให้การแก้ไขปัญหาที่ตรงจุดสำหรับนักเรียนที่มีปัญหา ให้โอกาสในการเสริมสร้างความรู้สำหรับผู้เรียนที่มีความสามารถสูง และให้การฝึกฝนทักษะอย่างสม่ำเสมอซึ่งช่วยสร้างความมั่นใจให้กับนักเรียนในการประยุกต์ใช้ทฤษฎีบทบานพับในสถานการณ์การแก้ปัญหาทางเรขาคณิตที่หลากหลาย
