
10 คิว
9th - 12th
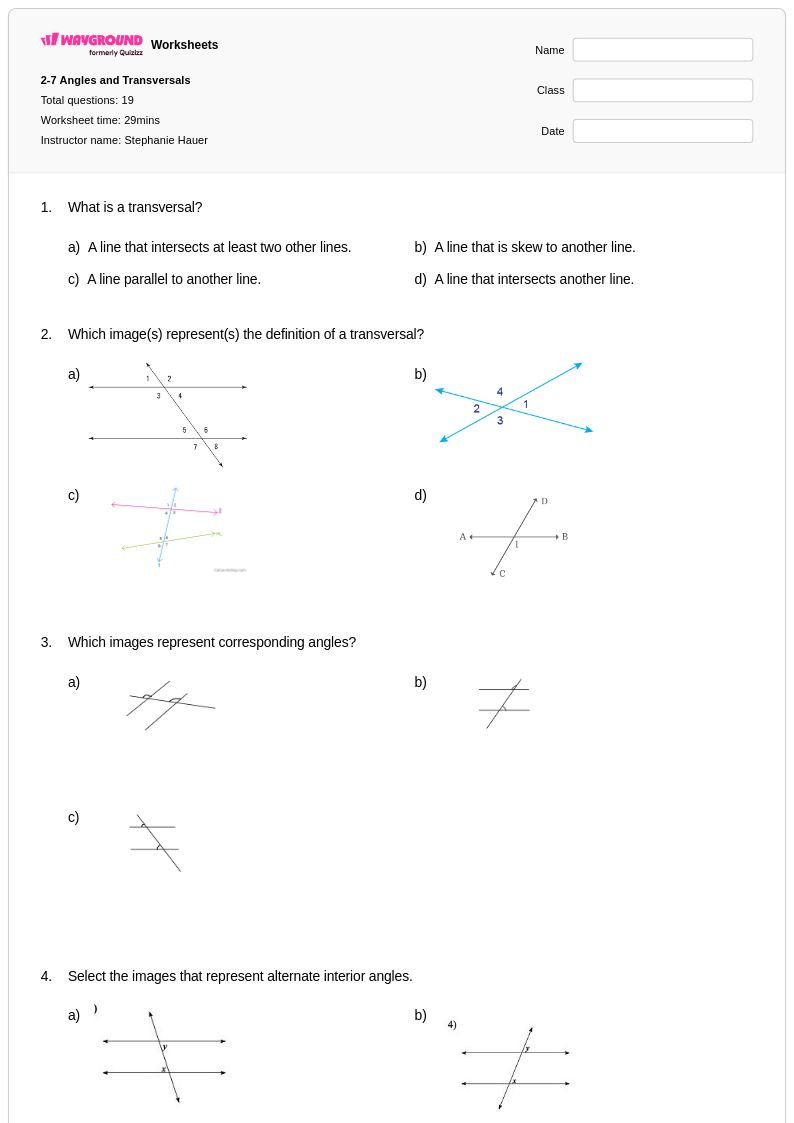
19 คิว
9th - 12th
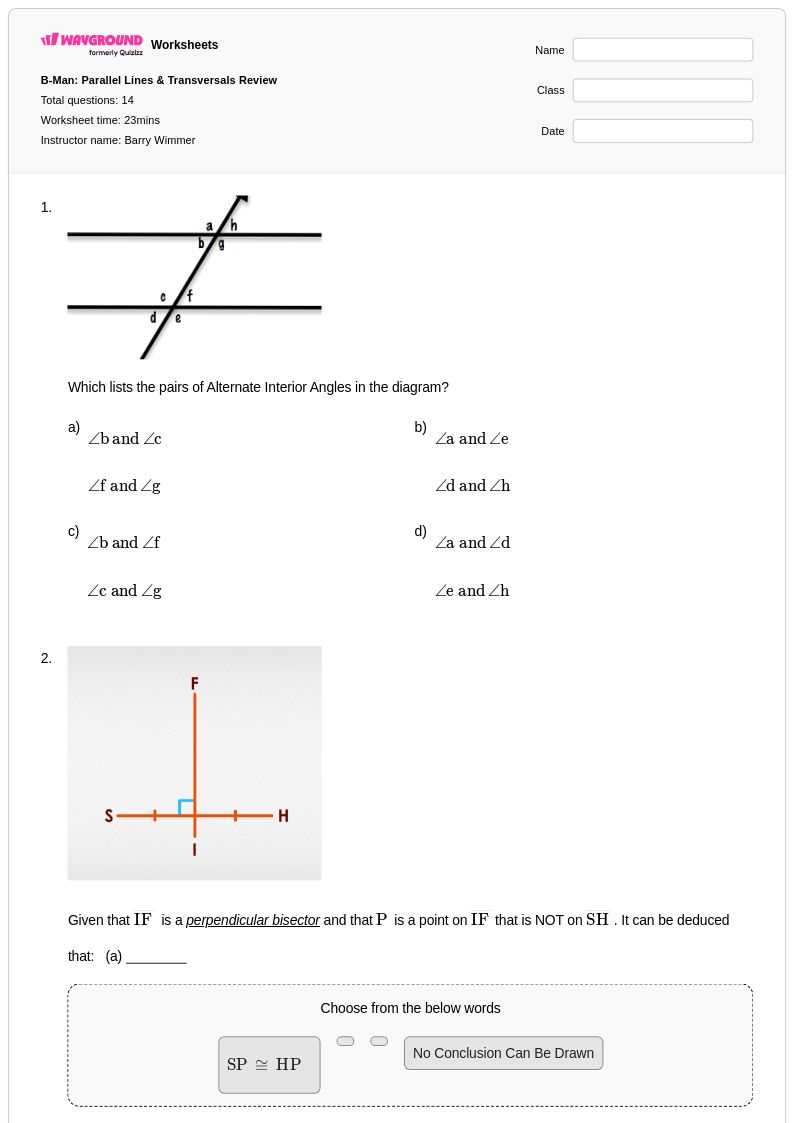
14 คิว
9th - 12th
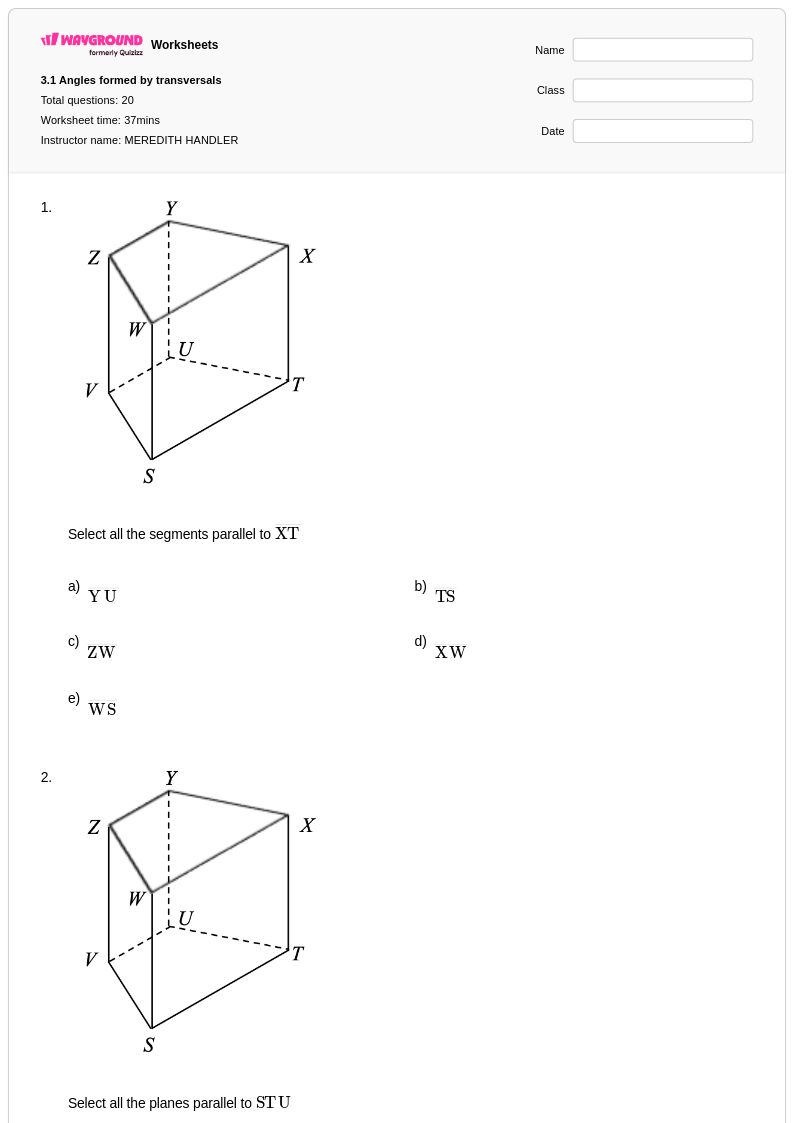
20 คิว
9th - 12th

18 คิว
9th - 12th
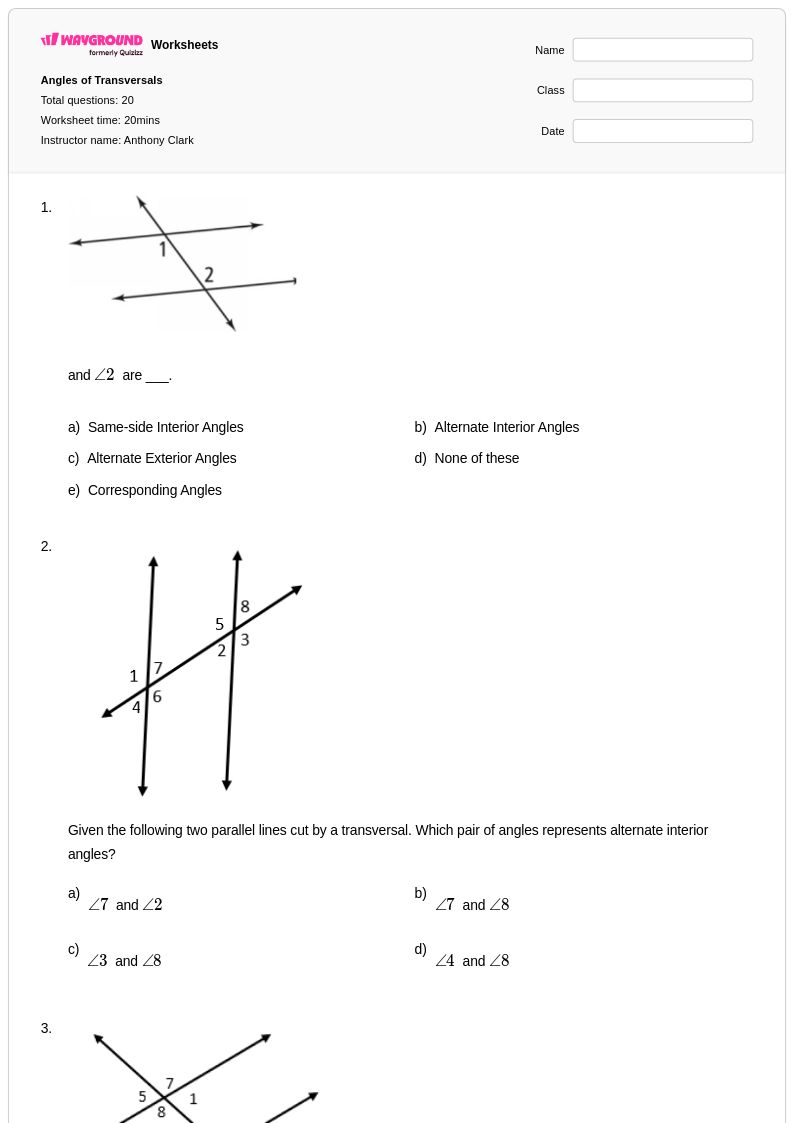
20 คิว
8th - Uni

20 คิว
8th - Uni
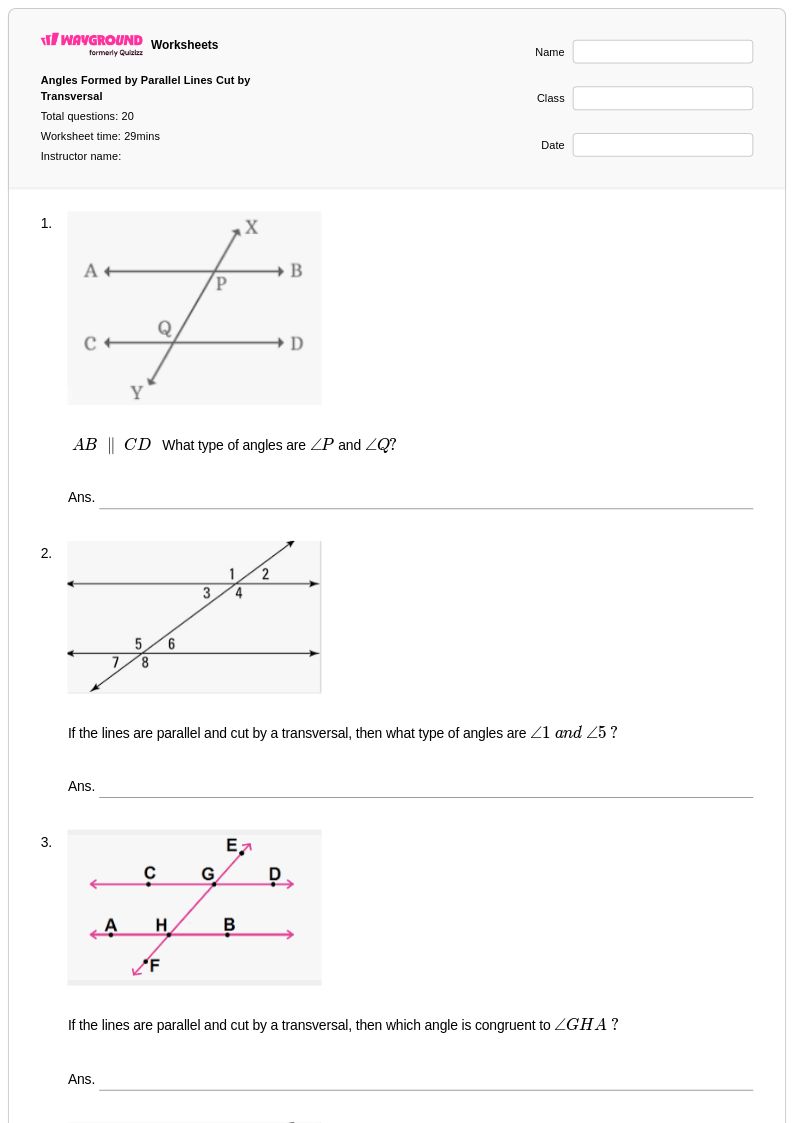
20 คิว
8th - 11th
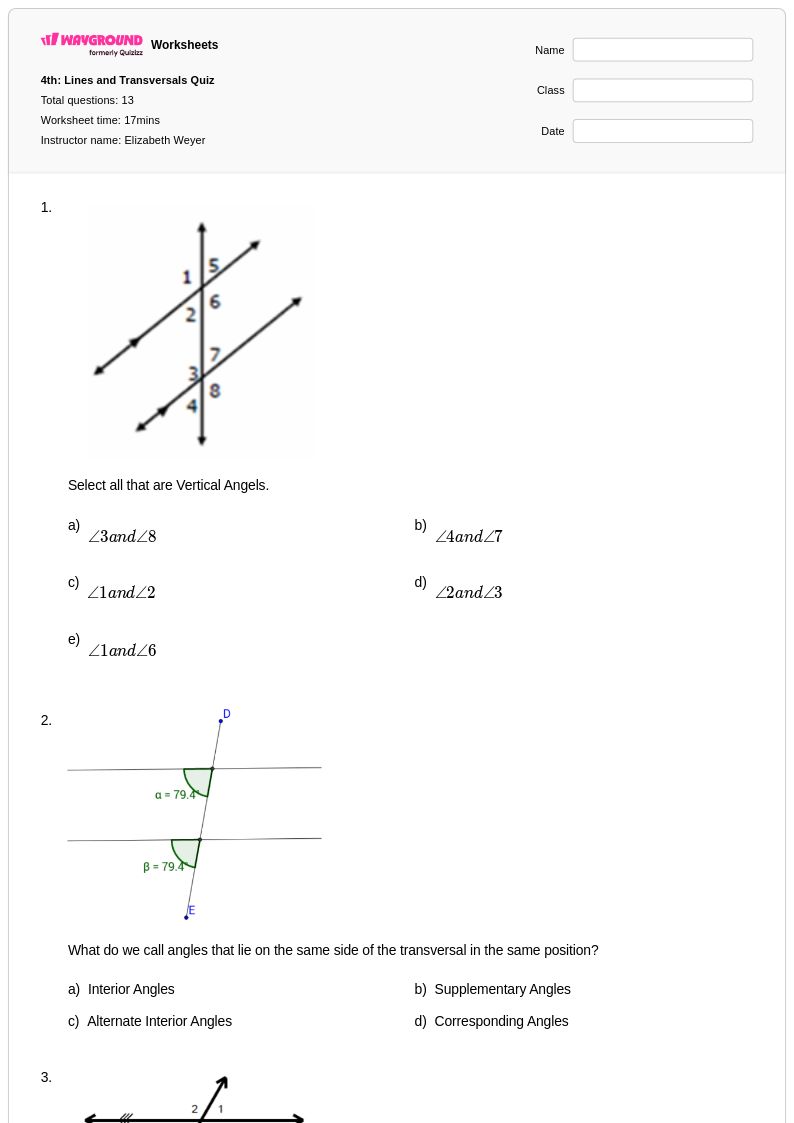
13 คิว
8th - 11th
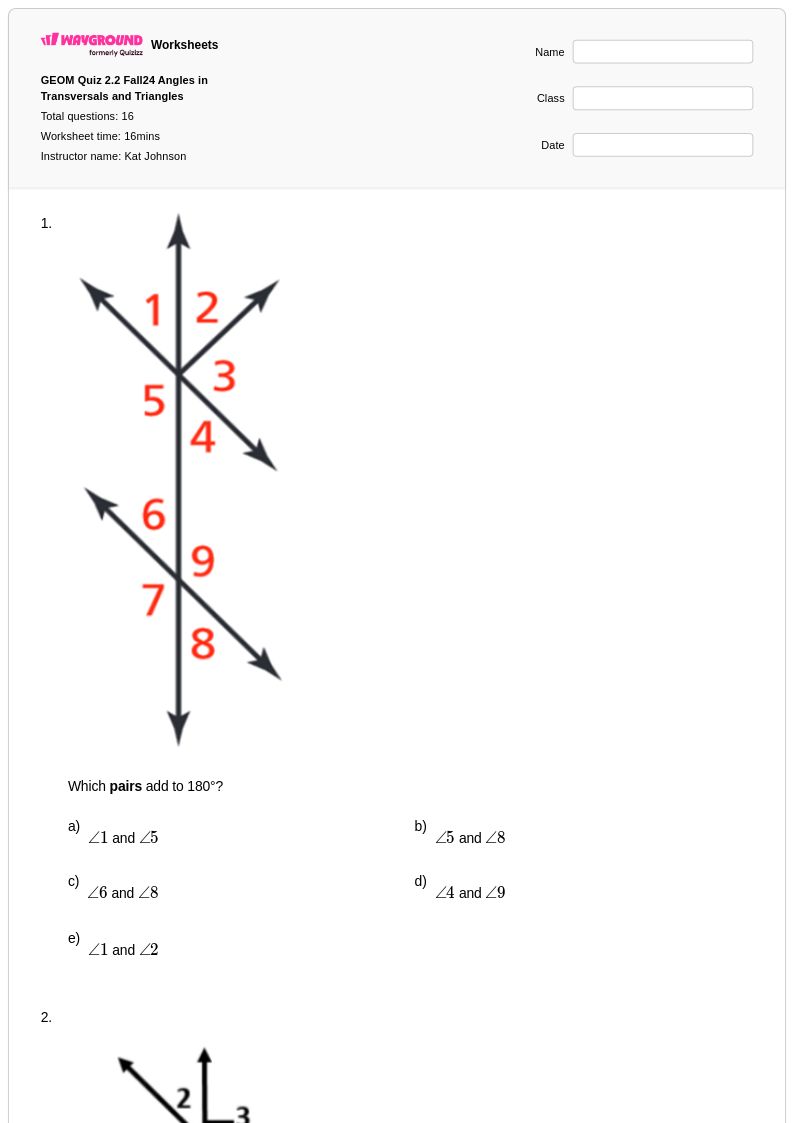
16 คิว
9th - 12th
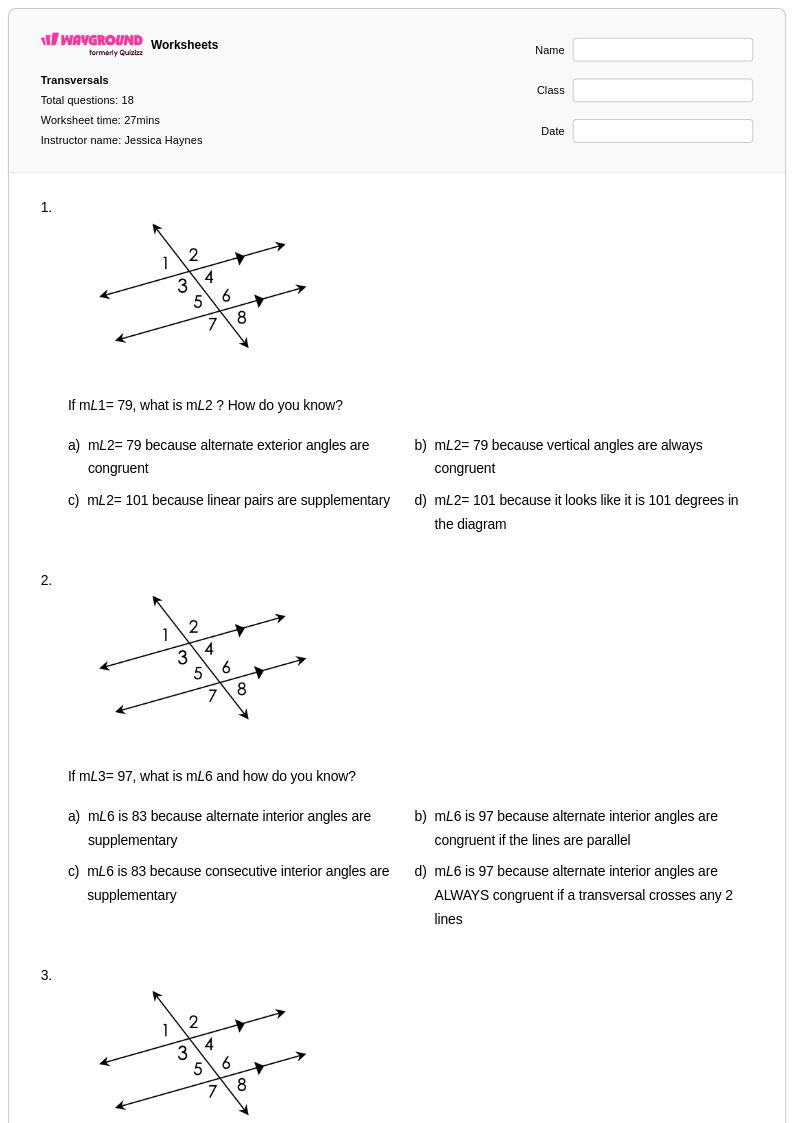
18 คิว
9th
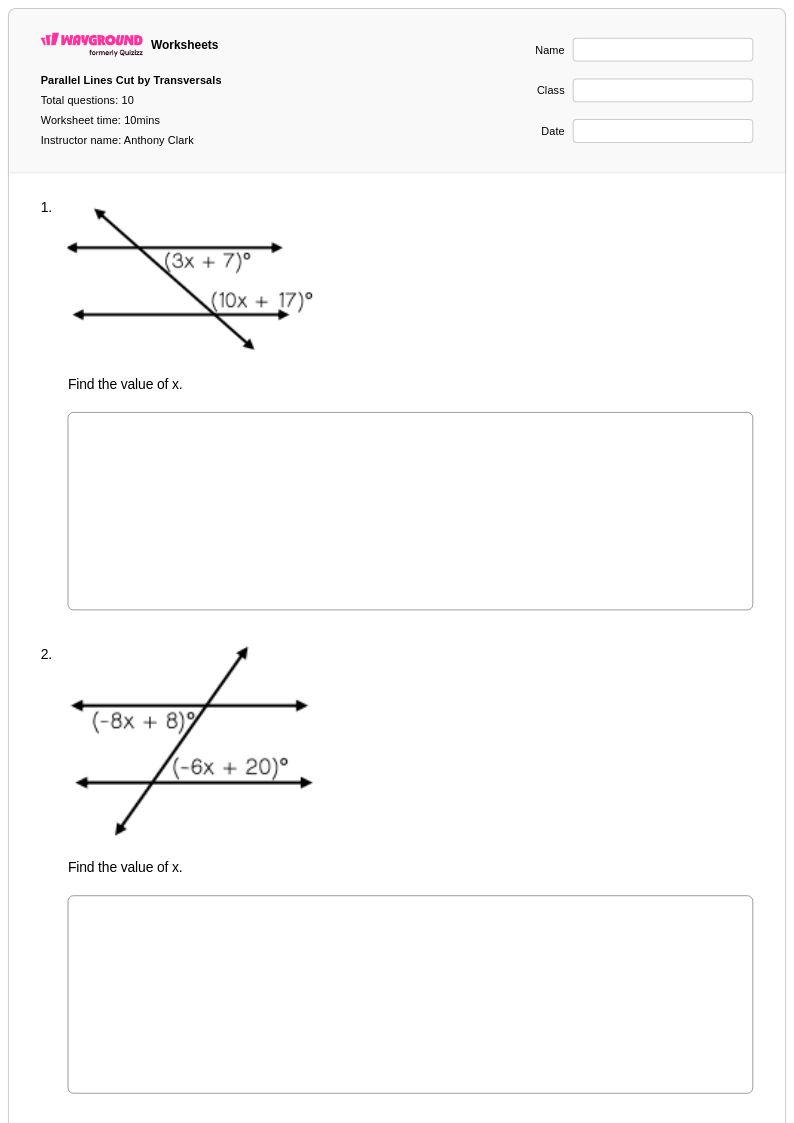
10 คิว
8th - Uni
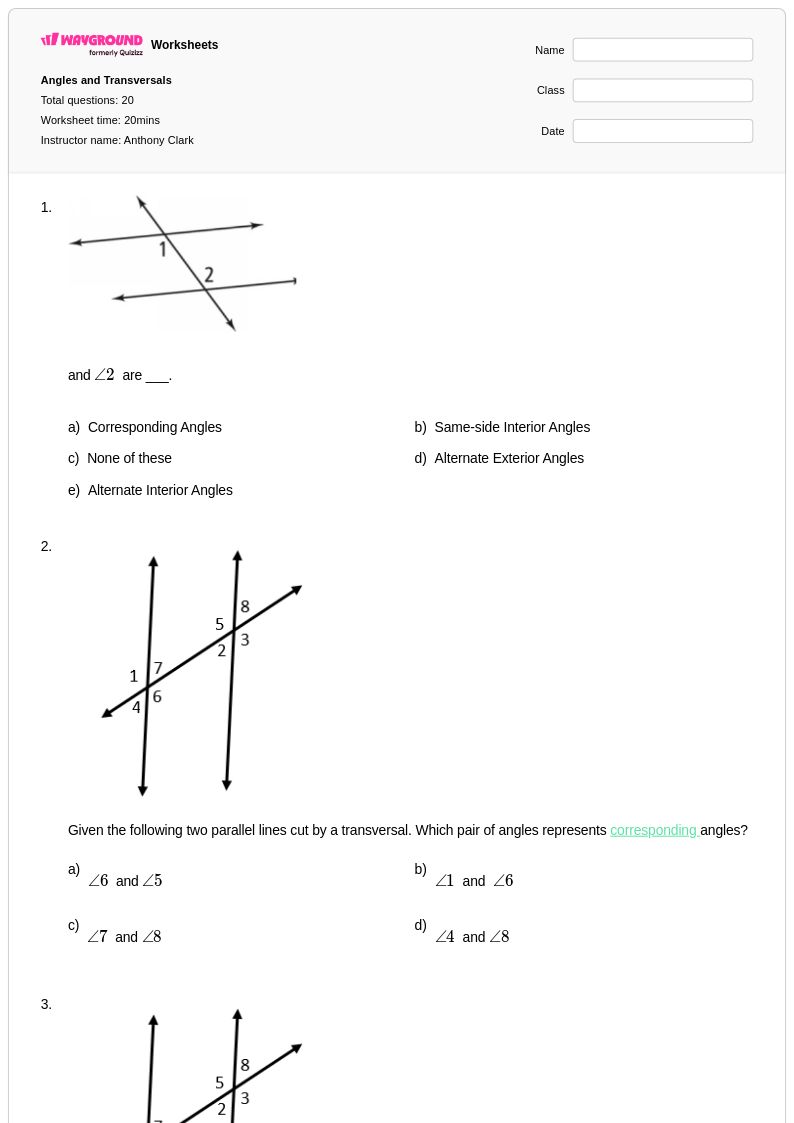
20 คิว
9th - Uni
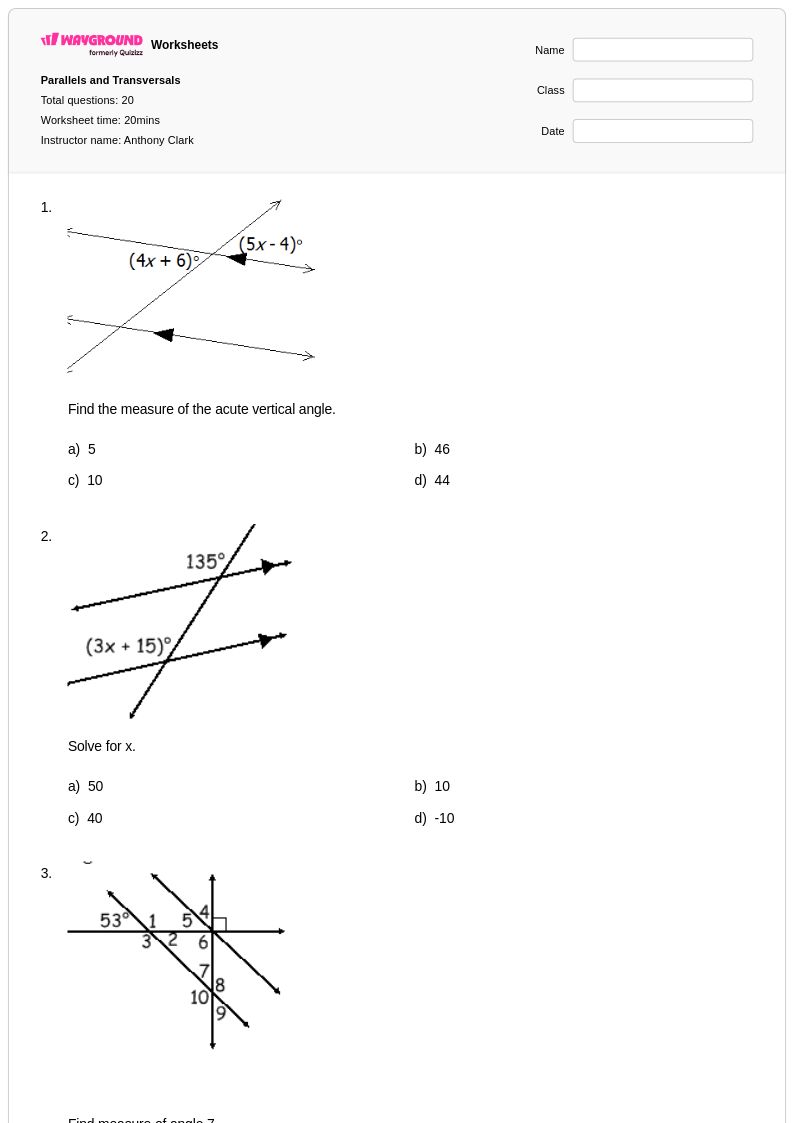
20 คิว
8th - Uni
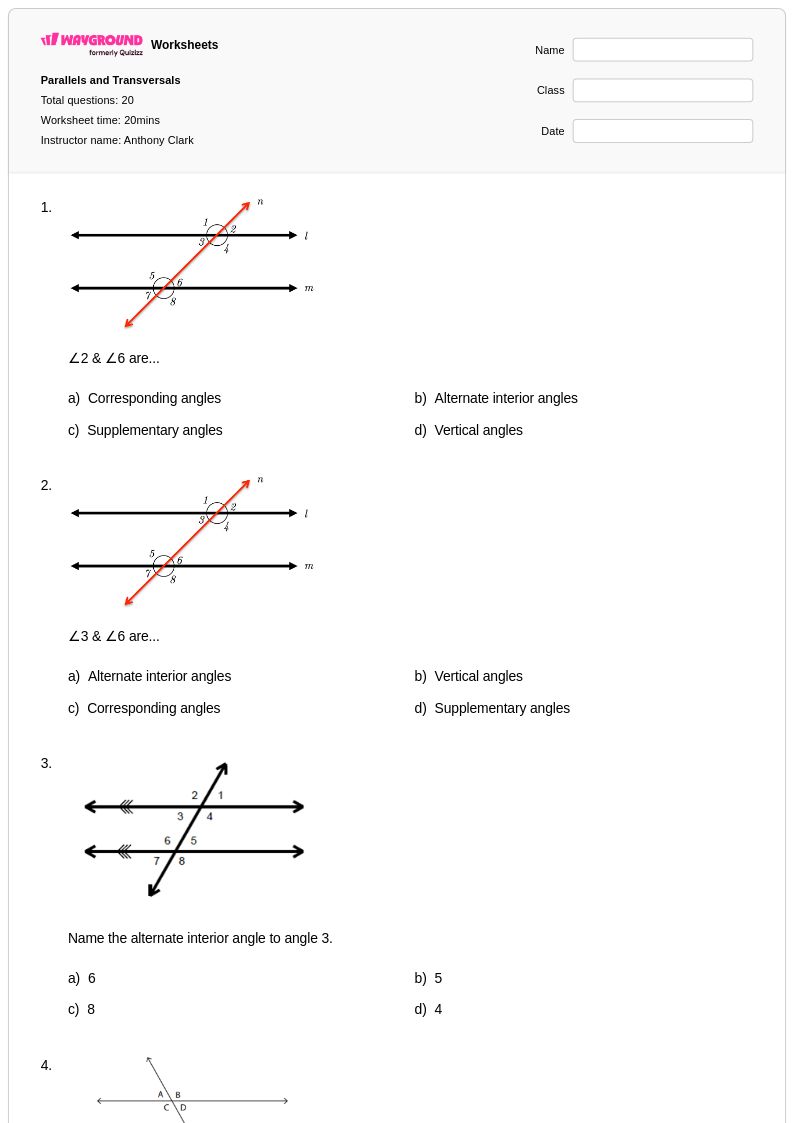
20 คิว
8th - Uni
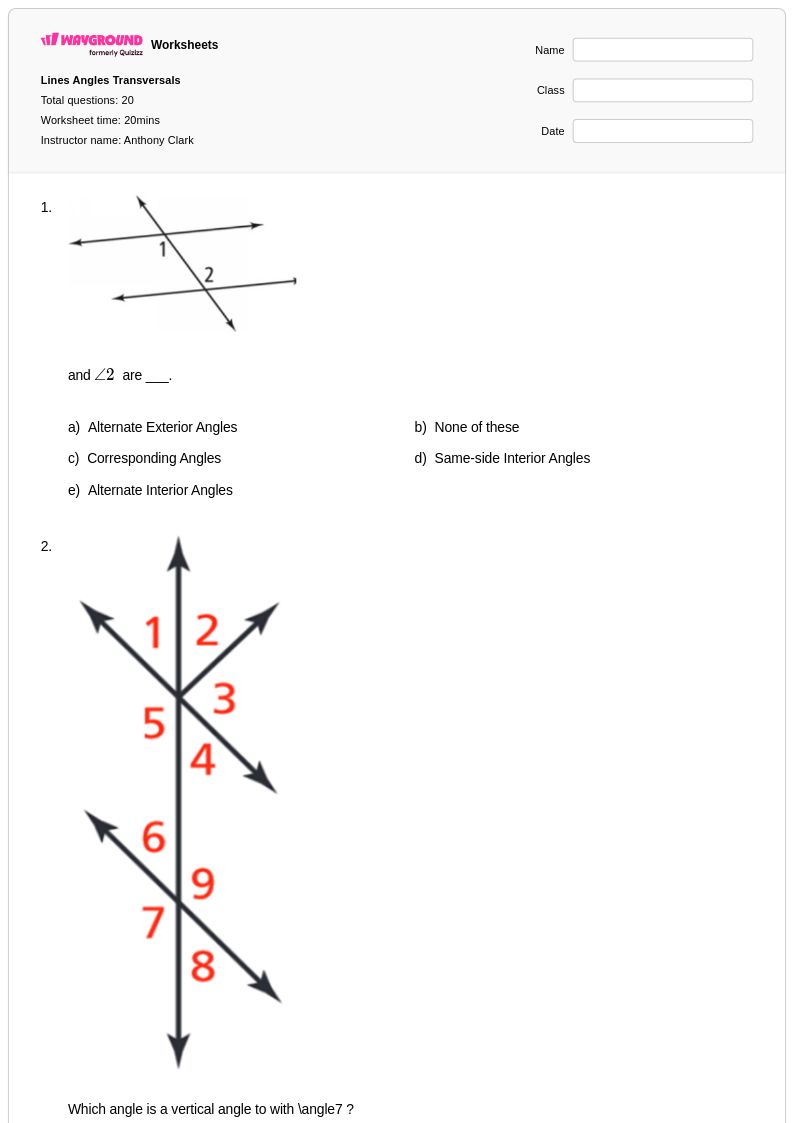
20 คิว
8th - Uni
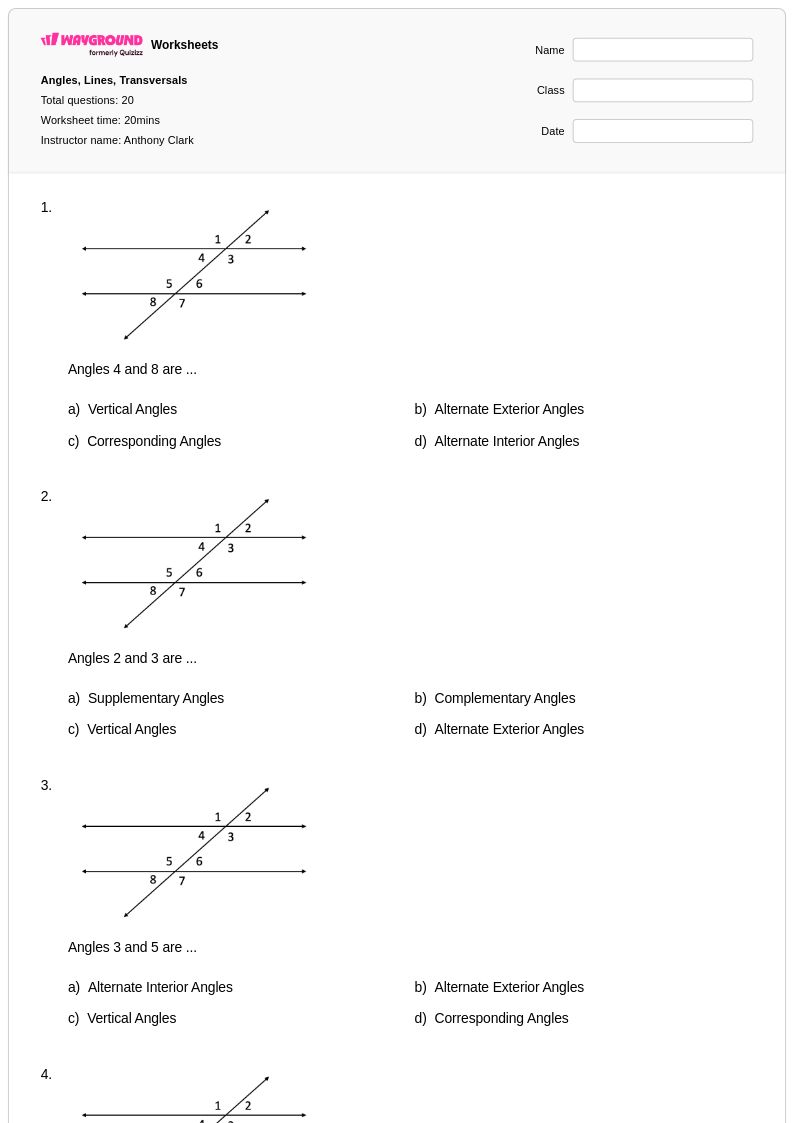
20 คิว
8th - Uni
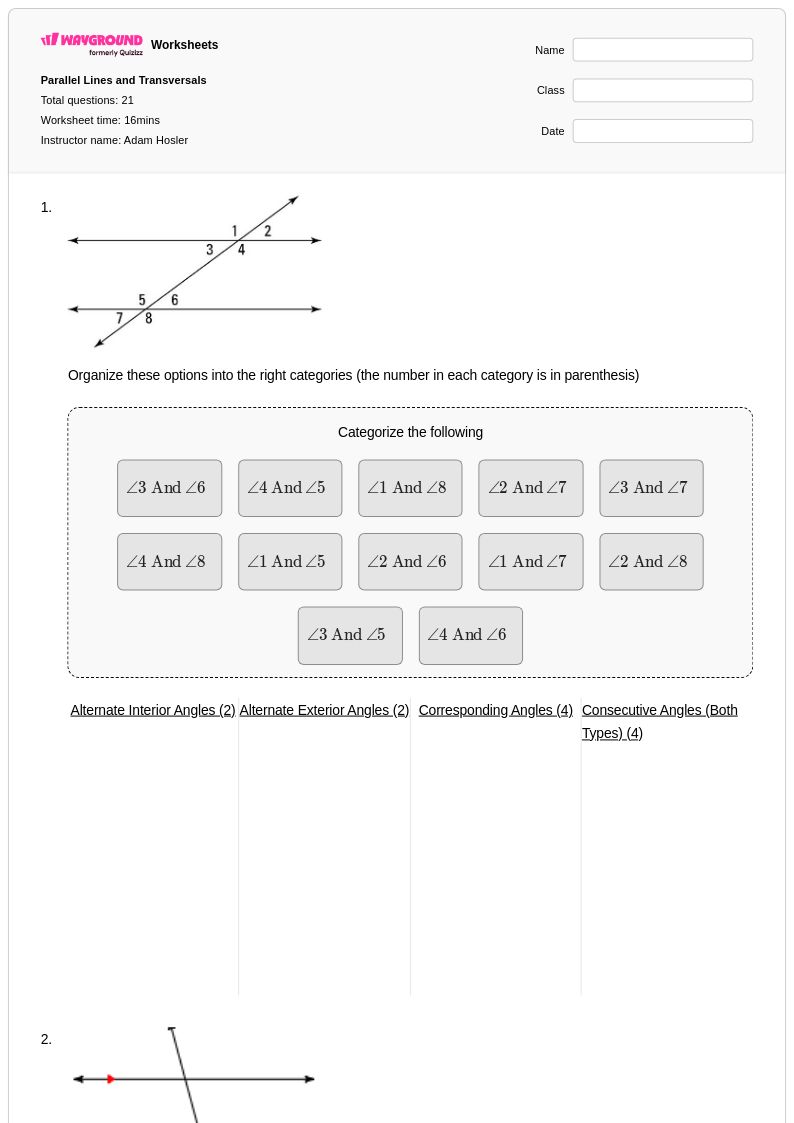
21 คิว
9th - 12th

10 คิว
8th - 12th
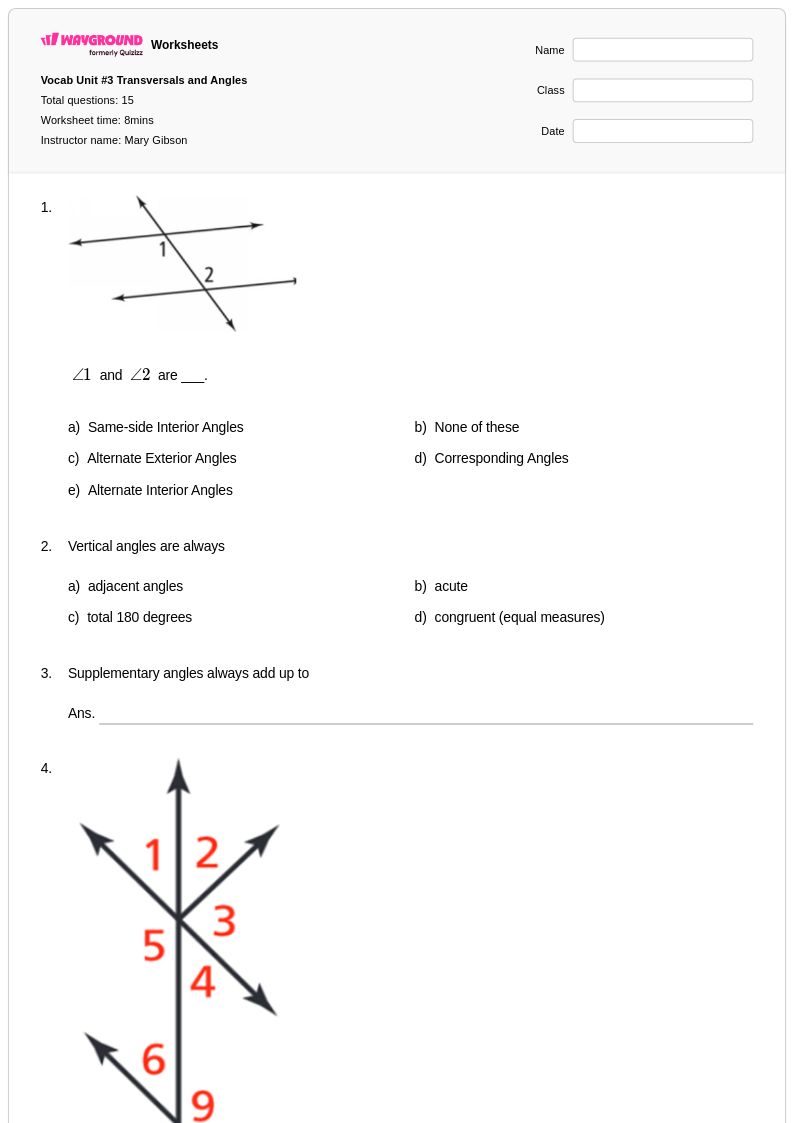
15 คิว
9th - 10th
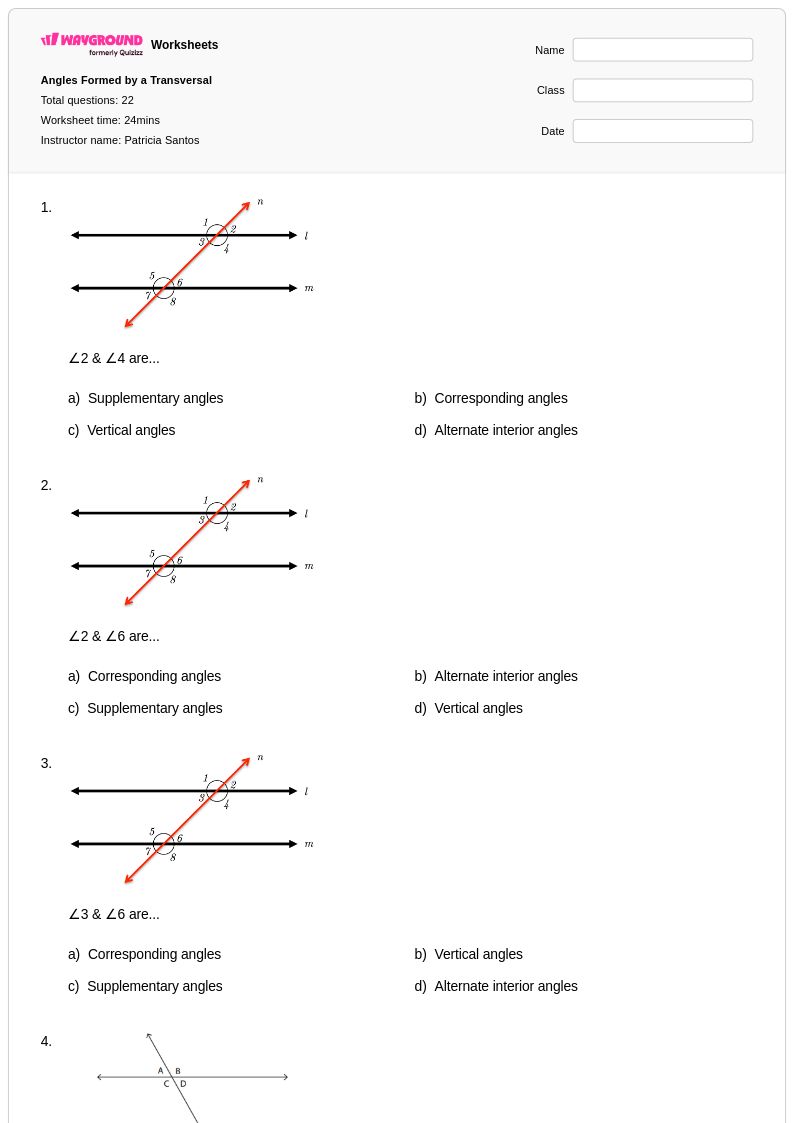
22 คิว
9th

10 คิว
9th - 12th
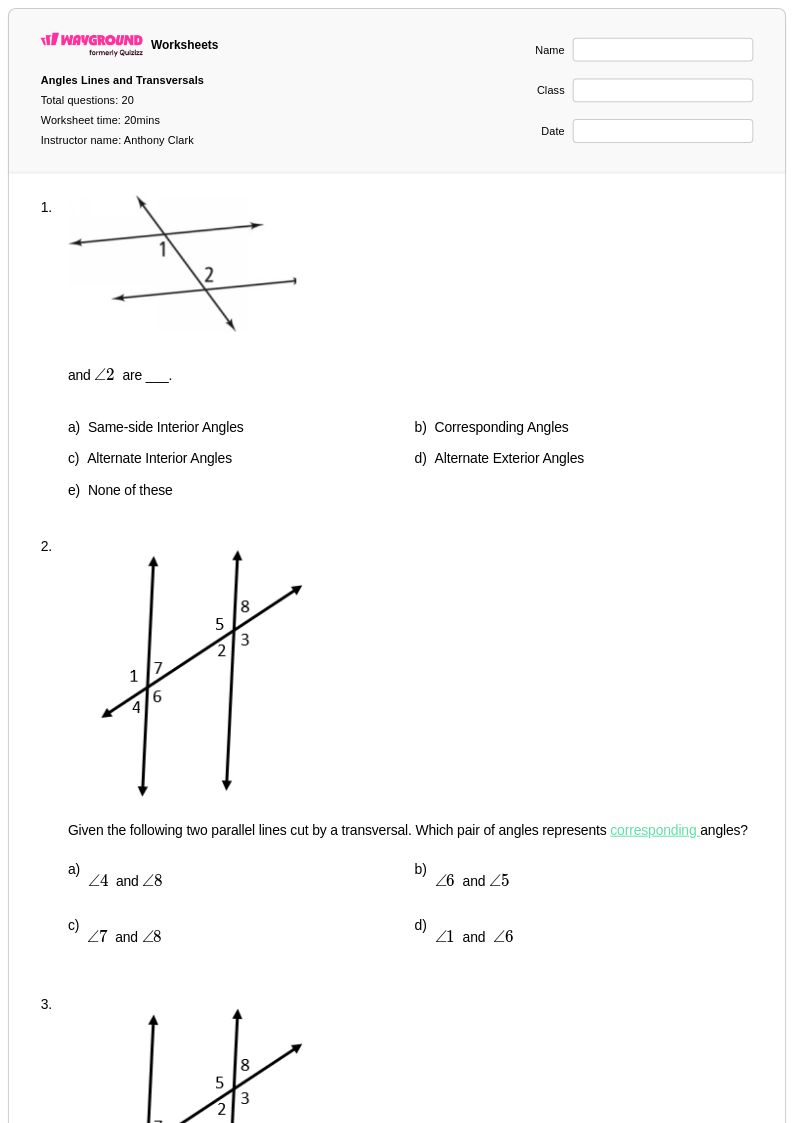
20 คิว
8th - Uni
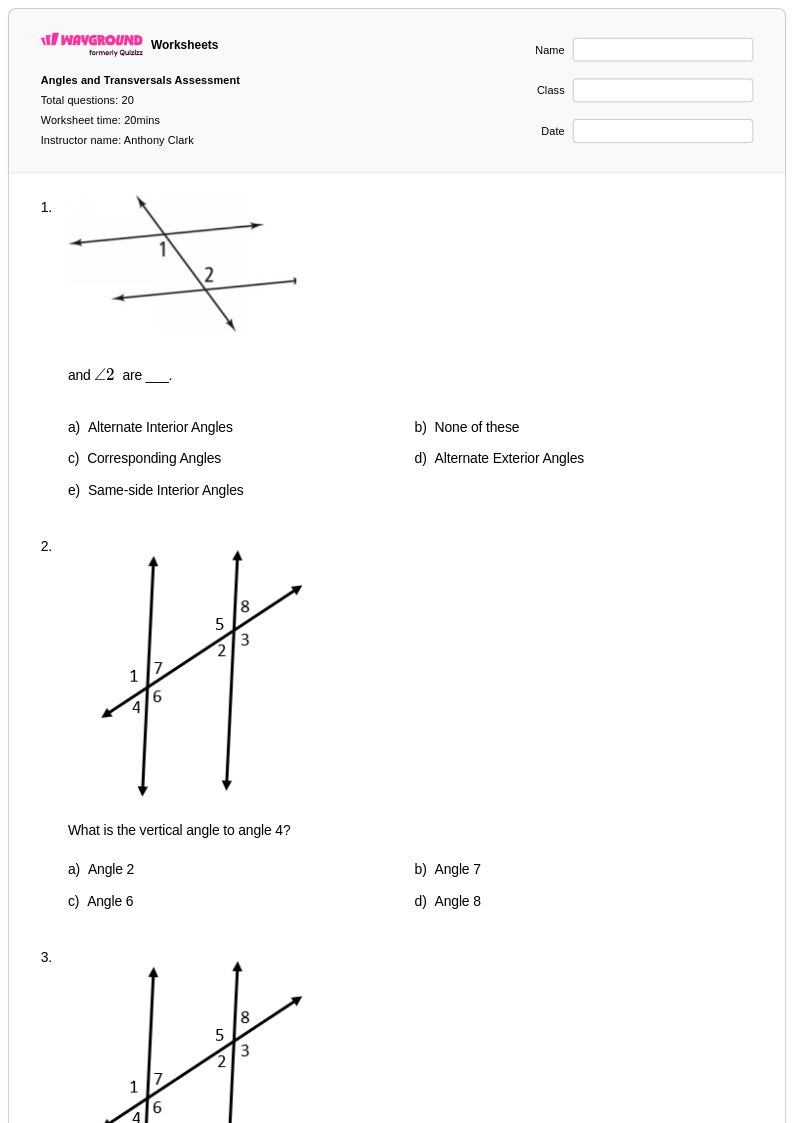
20 คิว
9th - Uni
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 9
สำรวจแผ่นงาน เส้นขวาง ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 9
แบบฝึกหัดเรื่องเส้นตัดสำหรับนักเรียนชั้น ม.3 จาก Wayground (เดิมคือ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมเกี่ยวกับแนวคิดพื้นฐานของเส้นที่ตัดกับเส้นอื่นสองเส้นขึ้นไป และความสัมพันธ์ของมุมที่เกิดขึ้น แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยเสริมสร้างความเข้าใจของนักเรียนเกี่ยวกับมุมที่สมนัยกัน มุมภายในและมุมภายนอกสลับกัน มุมภายในร่วม และคุณสมบัติที่เกิดขึ้นเมื่อเส้นตัดตัดกับเส้นขนาน แบบฝึกหัดมีโจทย์ฝึกฝนอย่างเป็นระบบที่ช่วยแนะนำนักเรียนในการระบุคู่มุม คำนวณขนาดมุมที่หายไป และประยุกต์ใช้ทฤษฎีบทเส้นตัดเพื่อแก้ปัญหาทางเรขาคณิตที่ซับซ้อน แบบฝึกหัดแต่ละชุดมีเฉลยคำตอบโดยละเอียด และมีให้ดาวน์โหลดเป็นไฟล์ PDF ที่พิมพ์ได้ฟรี ช่วยให้นักเรียนสามารถทำแบบฝึกหัดได้ตามจังหวะของตนเอง พร้อมทั้งสร้างความมั่นใจในการจดจำและประยุกต์ใช้ความสัมพันธ์ของเส้นตัดในบริบททางเรขาคณิตต่างๆ
Wayground (เดิมคือ Quizizz) ช่วยเสริมศักยภาพครูด้วยคลังแบบฝึกหัดเรื่องเส้นตัดที่สร้างโดยครูหลายล้านชุด ซึ่งสอดคล้องกับมาตรฐานคณิตศาสตร์ชั้น ม.3 โดยเฉพาะ แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูผู้สอนสามารถค้นหาแหล่งข้อมูลที่ตรงกับความต้องการหลักสูตรเฉพาะของตนได้อย่างรวดเร็ว ไม่ว่าจะเป็นการเน้นที่การระบุมุมพื้นฐานหรือการประยุกต์ใช้คุณสมบัติของเส้นตัดขวางขั้นสูงโดยใช้การพิสูจน์ ครูสามารถปรับแต่งแบบฝึกหัดเพื่อการสอนที่แตกต่างกันสำหรับผู้เรียนที่หลากหลาย โดยปรับความซับซ้อนและปริมาณของโจทย์เพื่อสนับสนุนทั้งกิจกรรมการแก้ไขและการเสริมสร้างความรู้ รูปแบบที่ยืดหยุ่น รวมถึงไฟล์ PDF ที่พิมพ์ได้และเวอร์ชันดิจิทัลแบบโต้ตอบ ช่วยให้การวางแผนบทเรียนง่ายขึ้น ในขณะเดียวกันก็มีช่องทางมากมายสำหรับการฝึกฝนทักษะ การประเมินผลระหว่างเรียน และการแทรกแซงที่ตรงเป้าหมาย เพื่อให้แน่ใจว่านักเรียนทุกคนเชี่ยวชาญความสัมพันธ์ทางเรขาคณิตที่สำคัญซึ่งเกิดจากเส้นตัดขวาง
