
26 คิว
9th - Uni
14 คิว
8th - Uni
11 คิว
10th - Uni

16 คิว
10th - Uni
14 คิว
10th - Uni

20 คิว
10th - Uni

10 คิว
9th - 12th
22 คิว
9th - 12th
20 คิว
9th - Uni
15 คิว
9th - 12th

20 คิว
10th - Uni
18 คิว
10th - 12th
10 คิว
9th - 12th
13 คิว
9th - 12th

20 คิว
10th - Uni

15 คิว
9th - Uni
15 คิว
10th - Uni
15 คิว
10th - Uni
25 คิว
6th - 12th
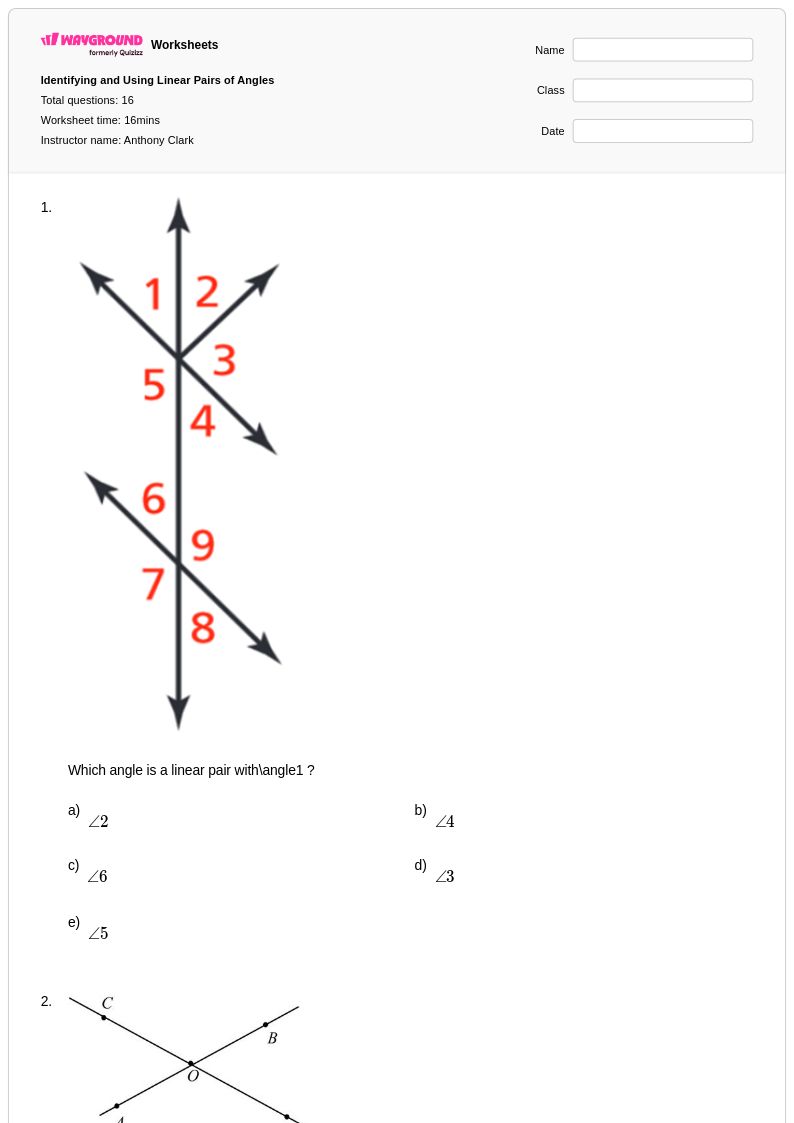
16 คิว
9th - Uni
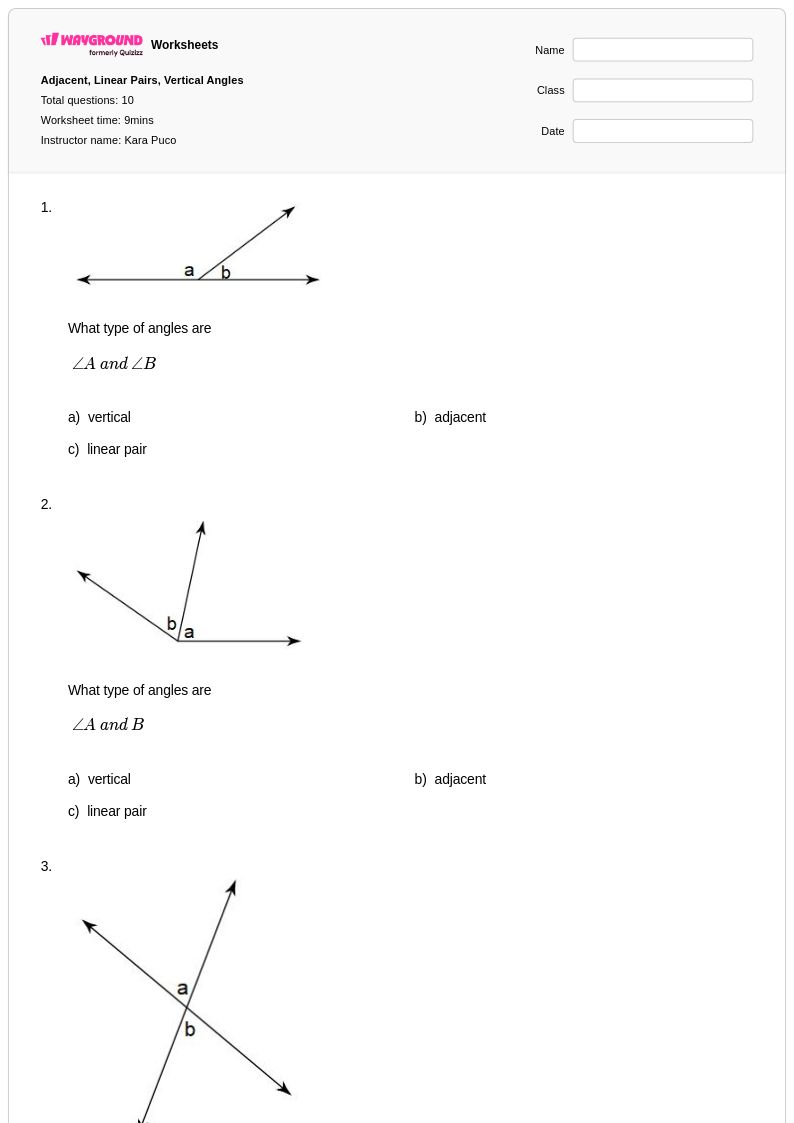
10 คิว
8th - 12th

25 คิว
6th - 12th
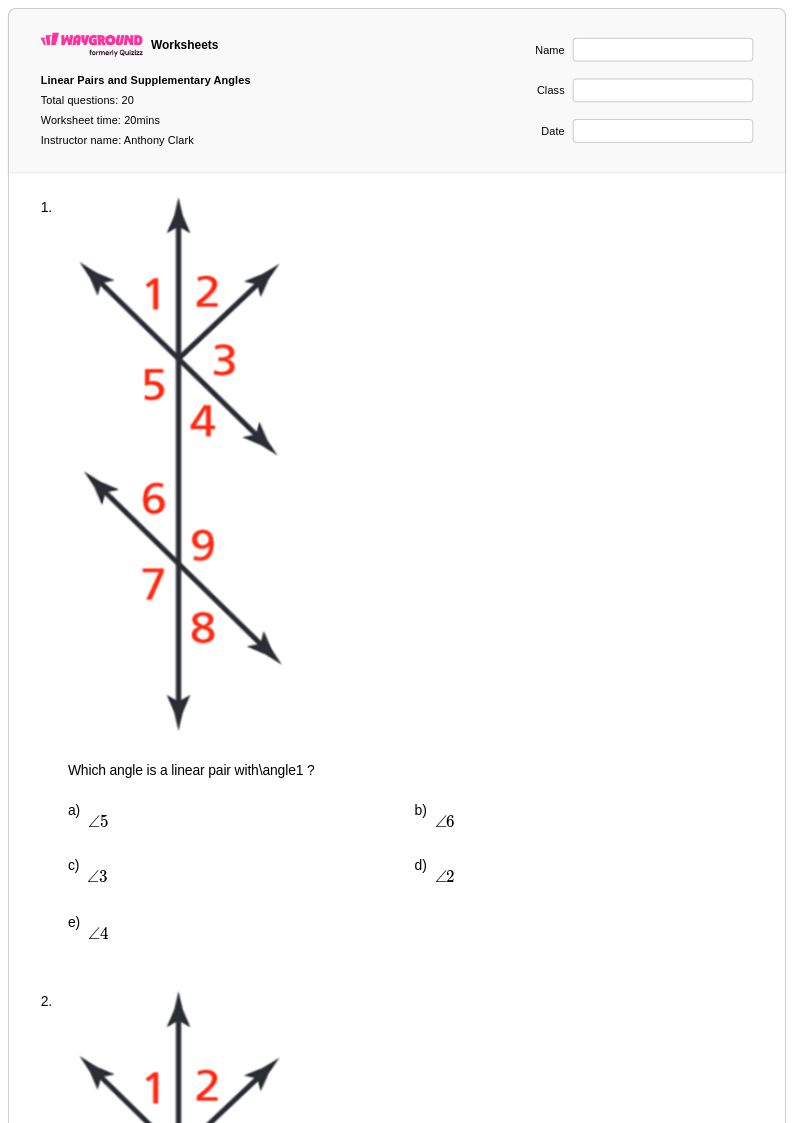
20 คิว
9th - Uni
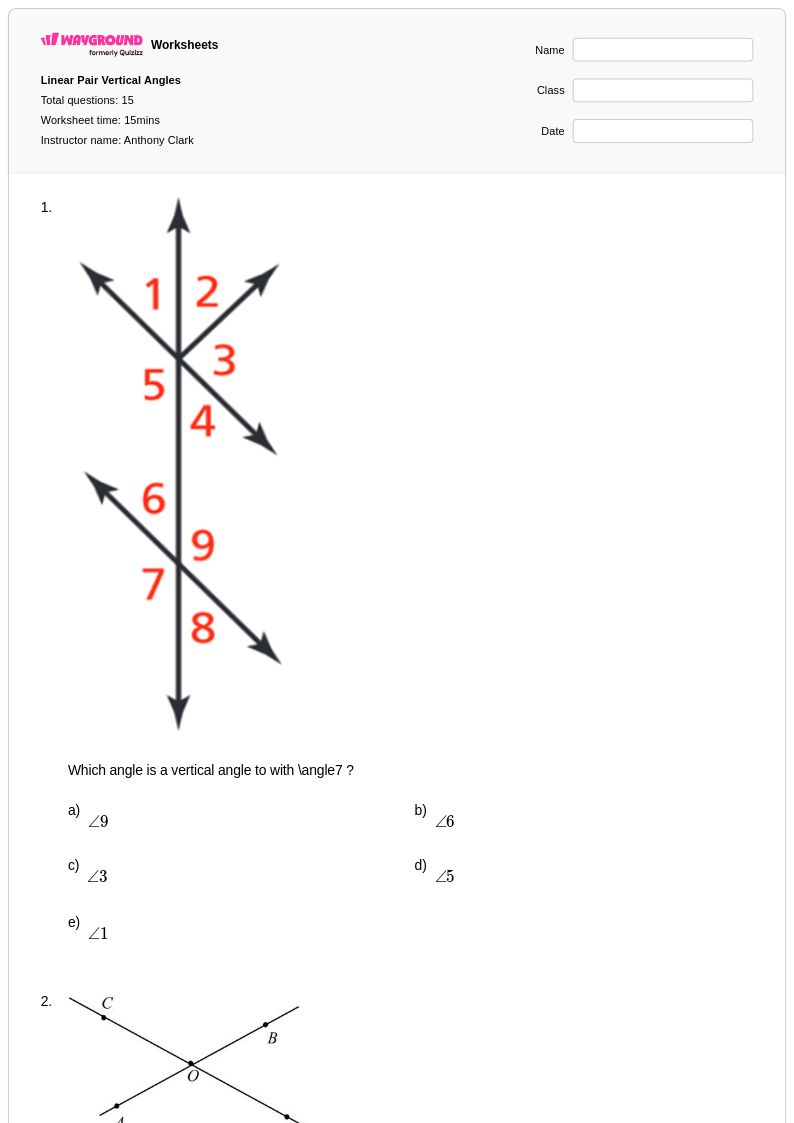
15 คิว
10th - Uni
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 11
สำรวจแผ่นงาน คู่เชิงเส้น ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 11
แบบฝึกหัดเรื่องมุมประชิดสำหรับวิชาคณิตศาสตร์ ม.4 (เกรด 11) เป็นแบบฝึกหัดสำคัญที่ช่วยให้นักเรียนพัฒนาทักษะการคิดเชิงเรขาคณิตขั้นสูง สื่อการเรียนรู้ที่ครอบคลุมนี้เน้นไปที่แนวคิดพื้นฐานที่ว่า มุมประชิดคือมุมที่อยู่ติดกันซึ่งด้านที่ไม่ใช่ด้านร่วมของมุมทั้งสองนั้นก่อเป็นเส้นตรงเดียวกัน และมีผลรวมของมุมทั้งสองเท่ากับ 180 องศาเสมอ แบบฝึกหัดของ Wayground มีให้เลือกมากมาย ท้าทายให้นักเรียนระบุมุมประชิดในรูปทรงเรขาคณิตที่ซับซ้อน หาค่ามุมที่ไม่ทราบค่าโดยใช้ความสัมพันธ์ของมุมประชิด และนำแนวคิดเหล่านี้ไปใช้ในการพิสูจน์ทฤษฎีบททางเรขาคณิต แบบฝึกหัดแต่ละชุดมีเฉลยอย่างละเอียดและสามารถดาวน์โหลดเป็นไฟล์ PDF ได้ฟรี โดยมีโจทย์ฝึกหัดที่หลากหลาย ตั้งแต่แบบฝึกหัดการระบุมุมพื้นฐานไปจนถึงแบบฝึกหัดการเขียนพิสูจน์ที่ซับซ้อน ซึ่งเตรียมความพร้อมให้นักเรียนสำหรับวิชาเรขาคณิตและตรีโกณมิติขั้นสูง
Wayground ซึ่งเดิมชื่อ Quizizz ช่วยให้ครูผู้สอนมีแหล่งข้อมูลเกี่ยวกับมุมประชิดที่สร้างโดยครูหลายล้านรายการ ซึ่งช่วยให้การวางแผนบทเรียนง่ายขึ้นและรองรับความต้องการการเรียนรู้ที่หลากหลาย ความสามารถในการค้นหาและกรองข้อมูลที่แข็งแกร่งของแพลตฟอร์มช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานหลักสูตรเฉพาะได้อย่างรวดเร็ว และสามารถปรับการสอนให้เหมาะสมกับความสามารถของนักเรียนแต่ละคนได้ สื่อการเรียนรู้ที่หลากหลายเหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์พิมพ์และไฟล์ PDF ดิจิทัล ทำให้สามารถบูรณาการเข้ากับการเรียนการสอนในห้องเรียนแบบดั้งเดิมหรือการเรียนรู้ทางไกลได้อย่างราบรื่น ครูสามารถปรับแต่งแบบฝึกหัดที่มีอยู่หรือรวมแหล่งข้อมูลหลายแหล่งเข้าด้วยกันเพื่อสร้างชุดแบบฝึกหัดที่ครอบคลุม ซึ่งจะช่วยแก้ไขปัญหาสำหรับนักเรียนที่เรียนรู้ช้า เพิ่มพูนความรู้สำหรับผู้เรียนที่มีความสามารถสูง และฝึกฝนทักษะเฉพาะด้านที่เสริมสร้างความสัมพันธ์ทางเรขาคณิตที่สำคัญที่นักเรียนจำเป็นต้องเชี่ยวชาญก่อนที่จะก้าวไปสู่หลักสูตรคณิตศาสตร์ระดับสูงขึ้น
