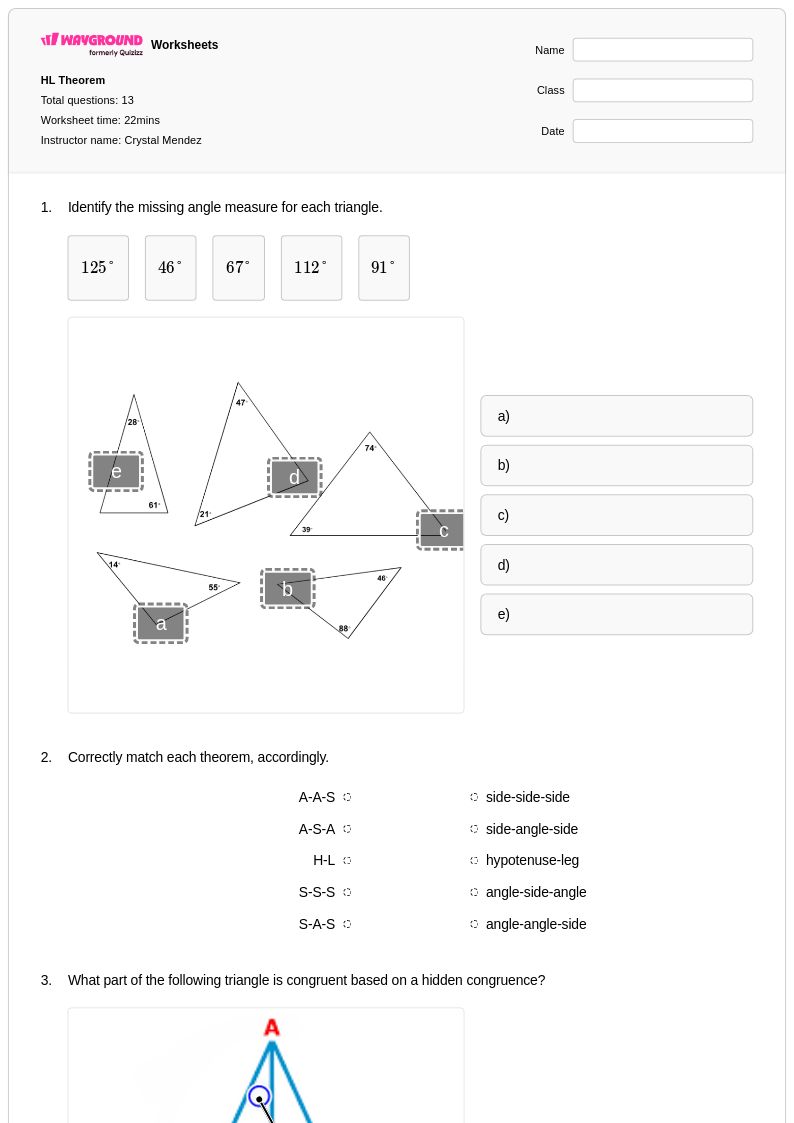
13 คิว
10th
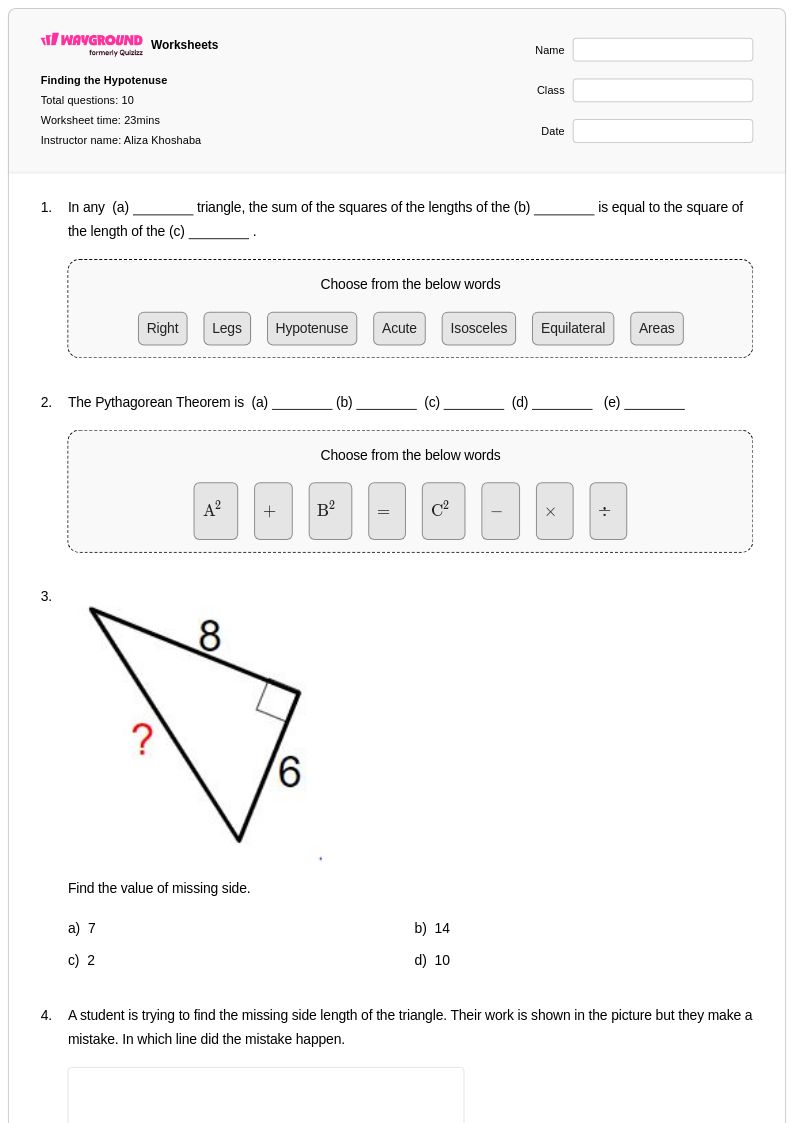
10 คิว
8th

10 คิว
8th
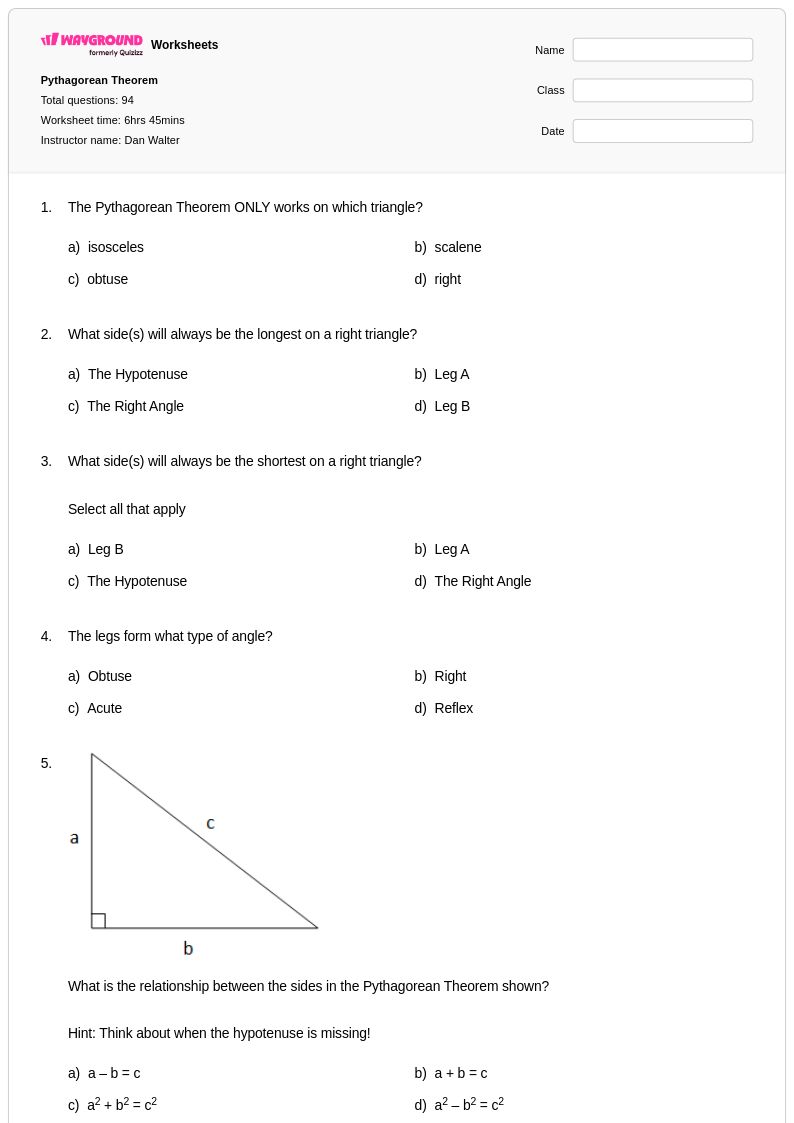
94 คิว
8th

20 คิว
8th
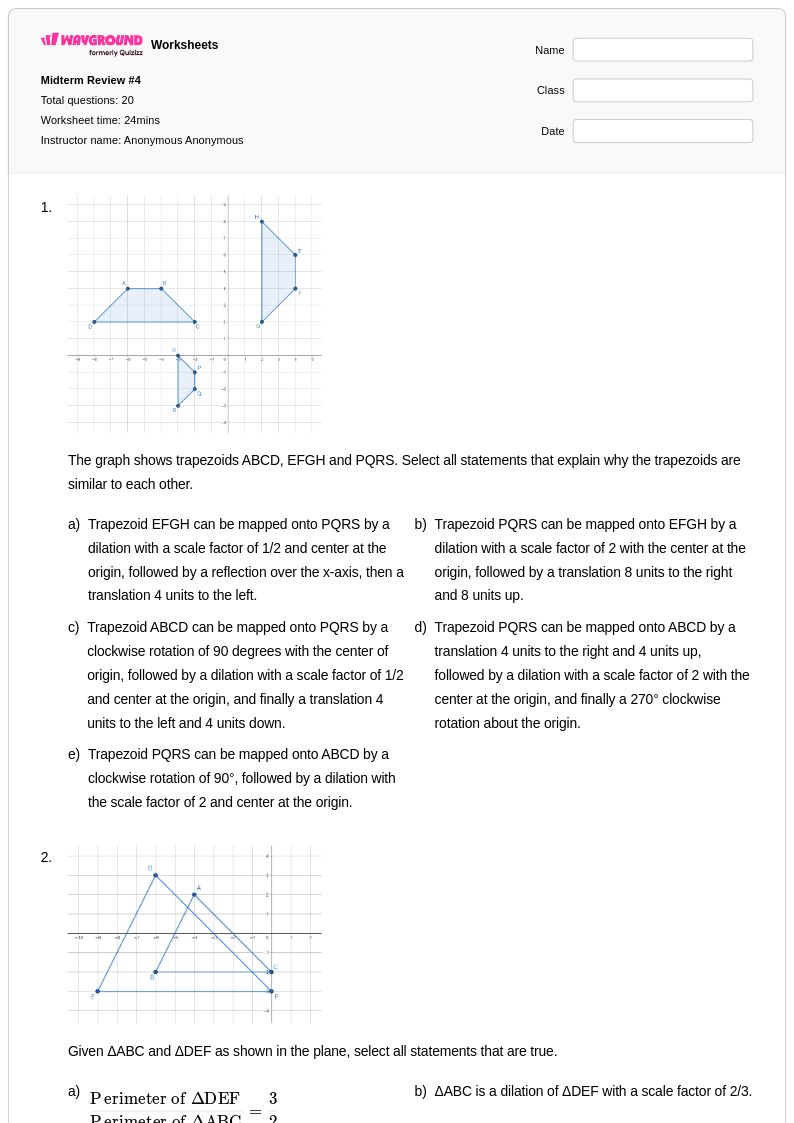
20 คิว
10th
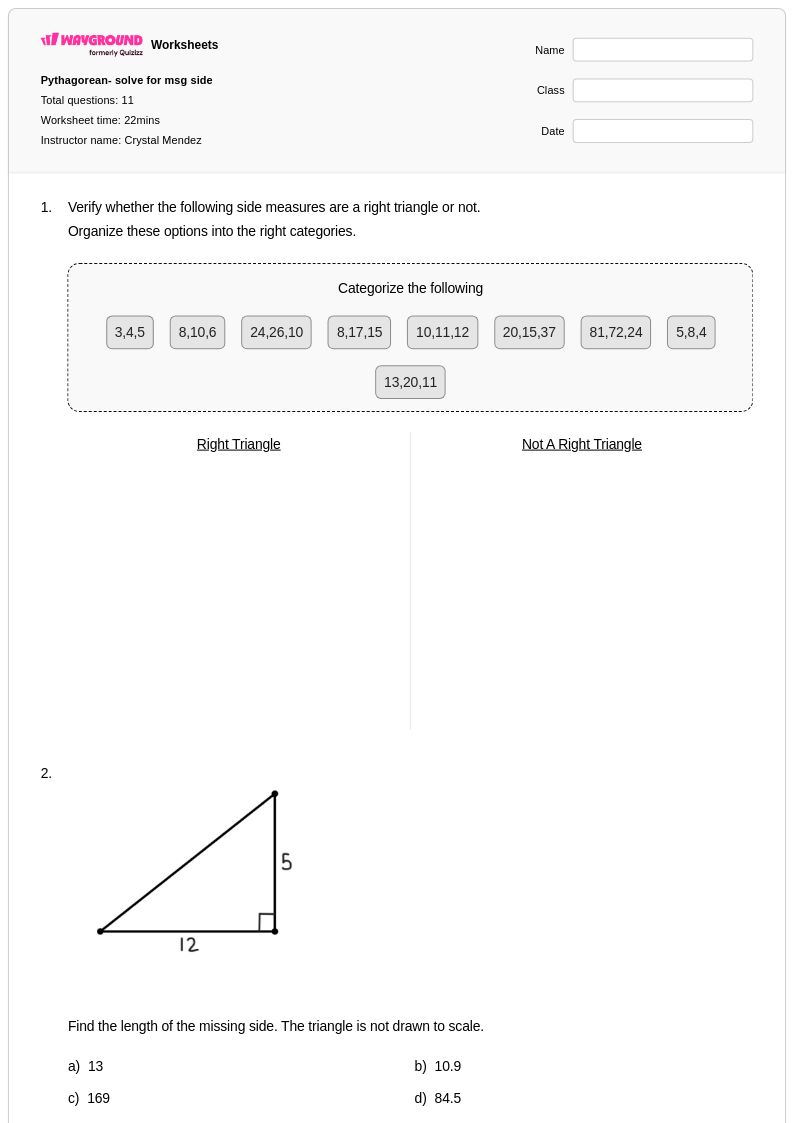
11 คิว
10th
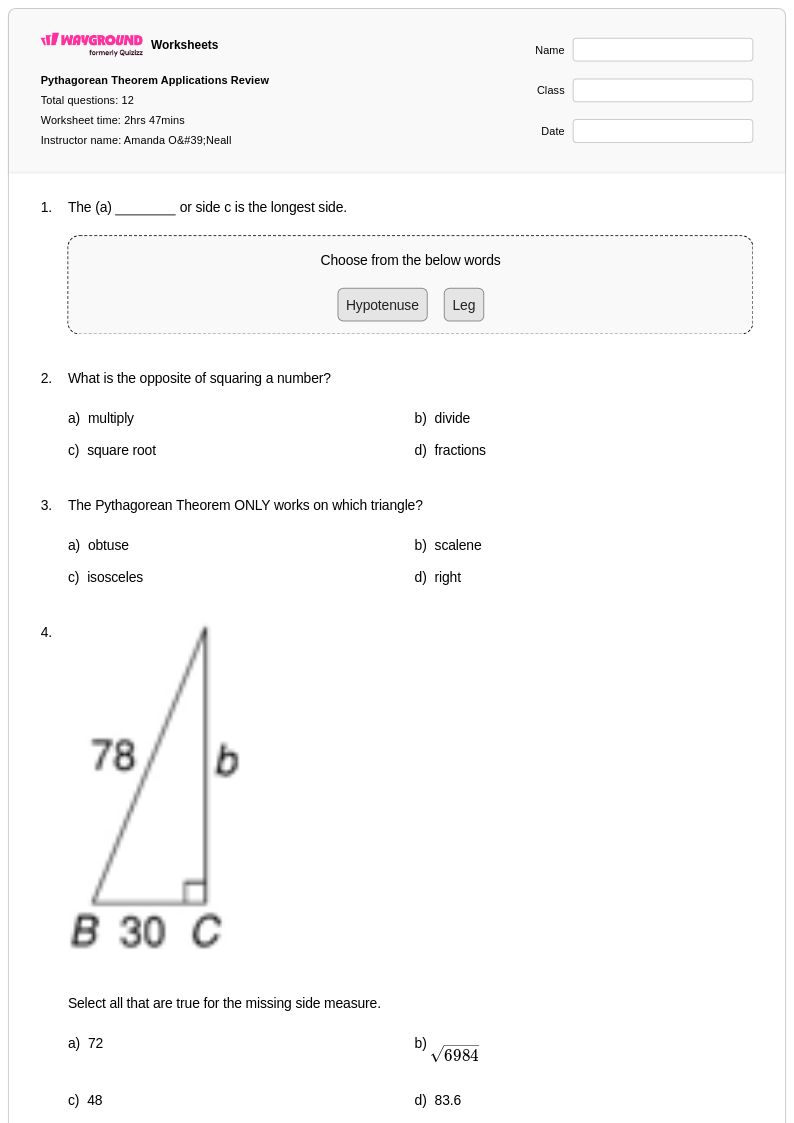
12 คิว
8th
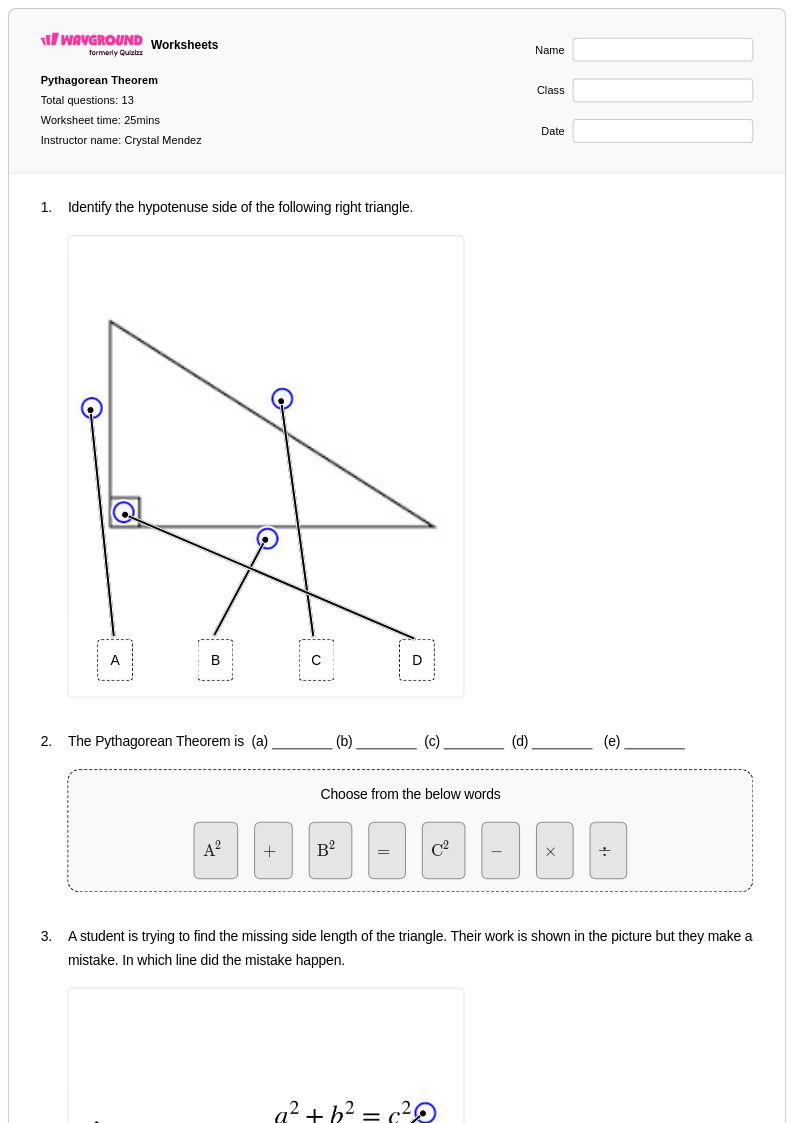
13 คิว
10th

21 คิว
8th

16 คิว
8th
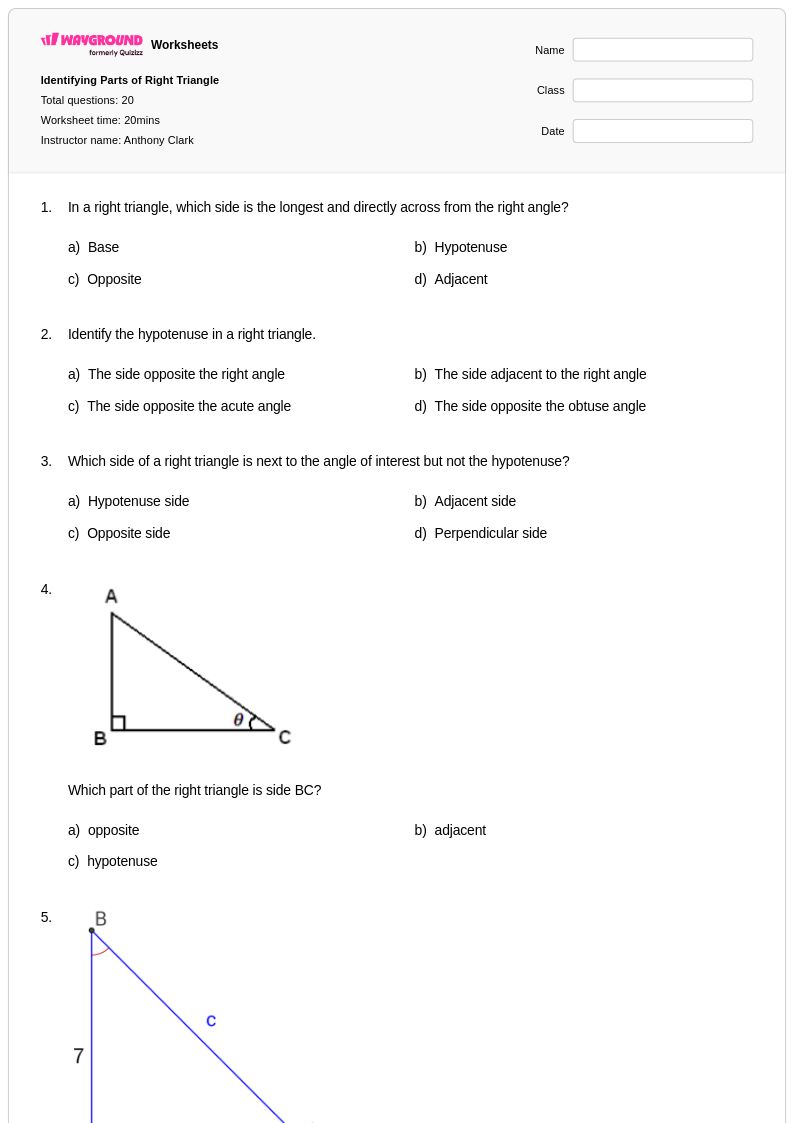
20 คิว
9th - Uni
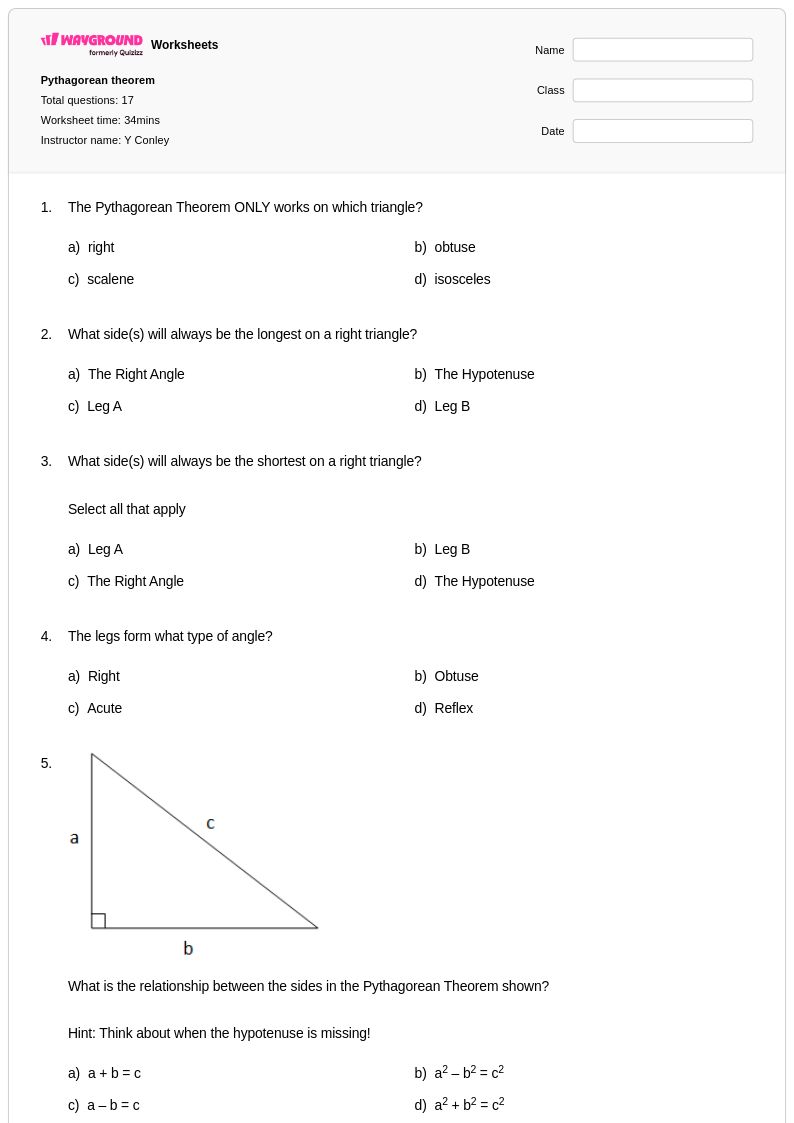
17 คิว
8th
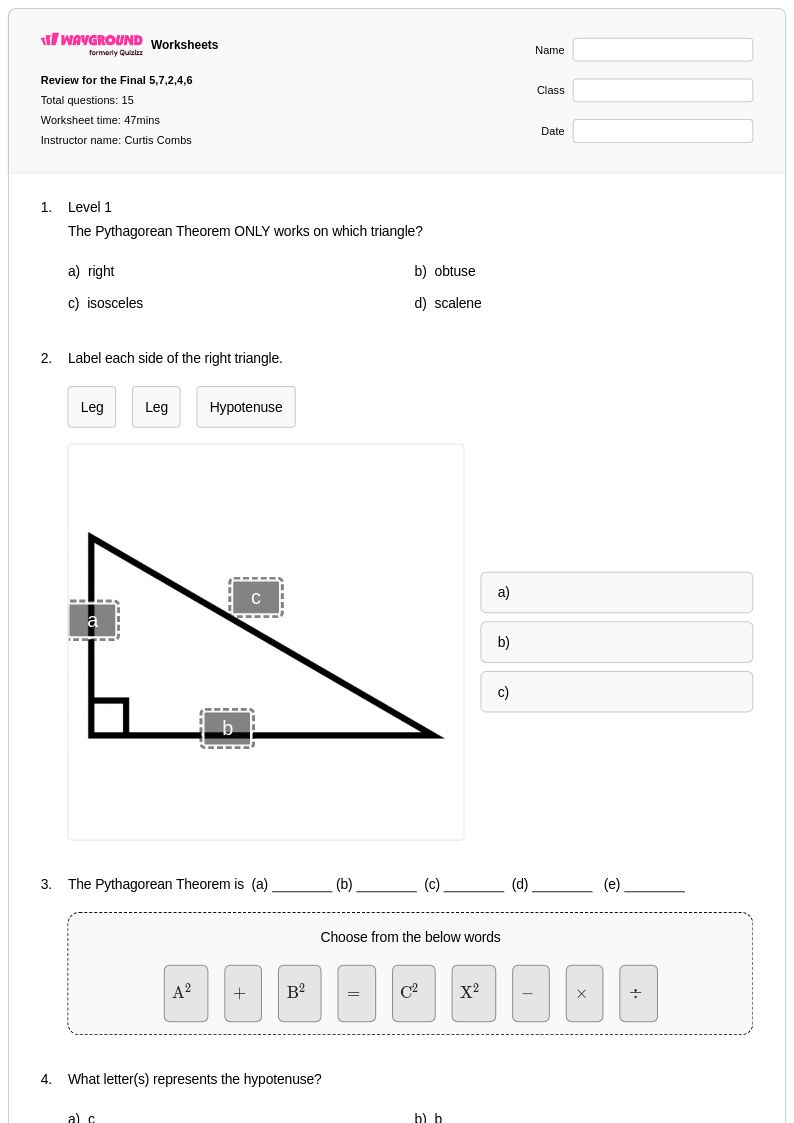
15 คิว
9th - 12th
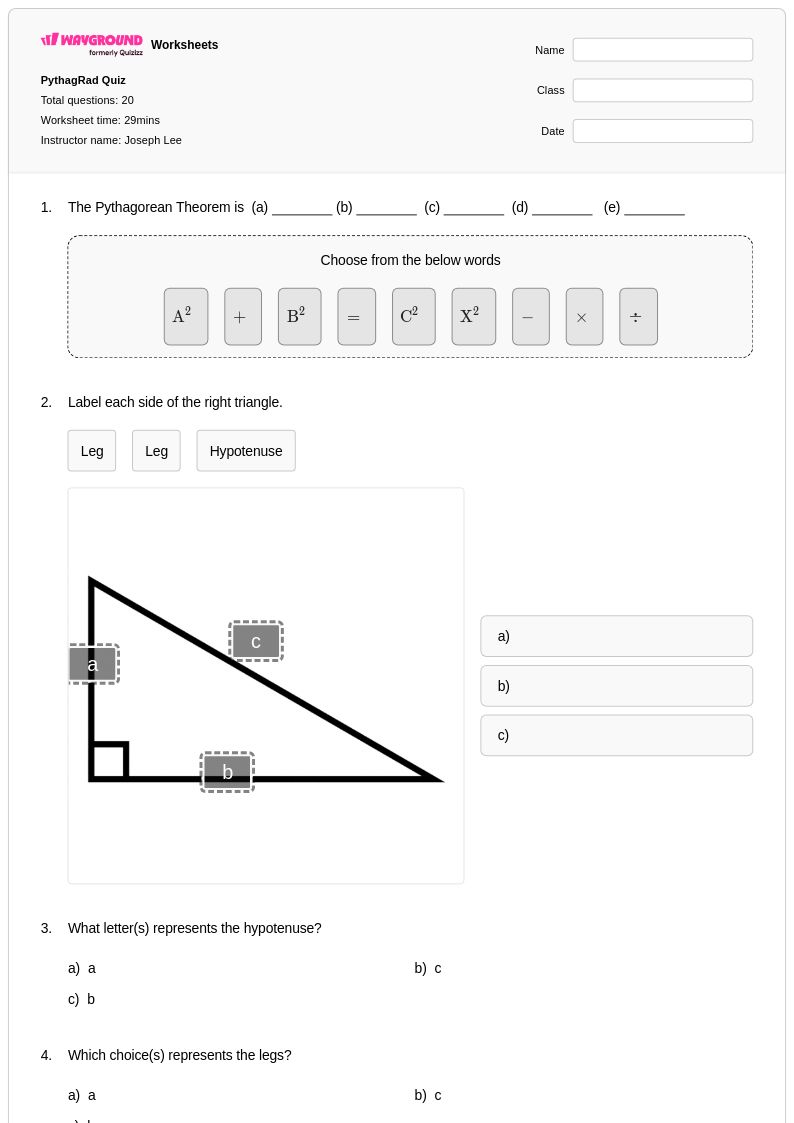
20 คิว
8th

12 คิว
10th
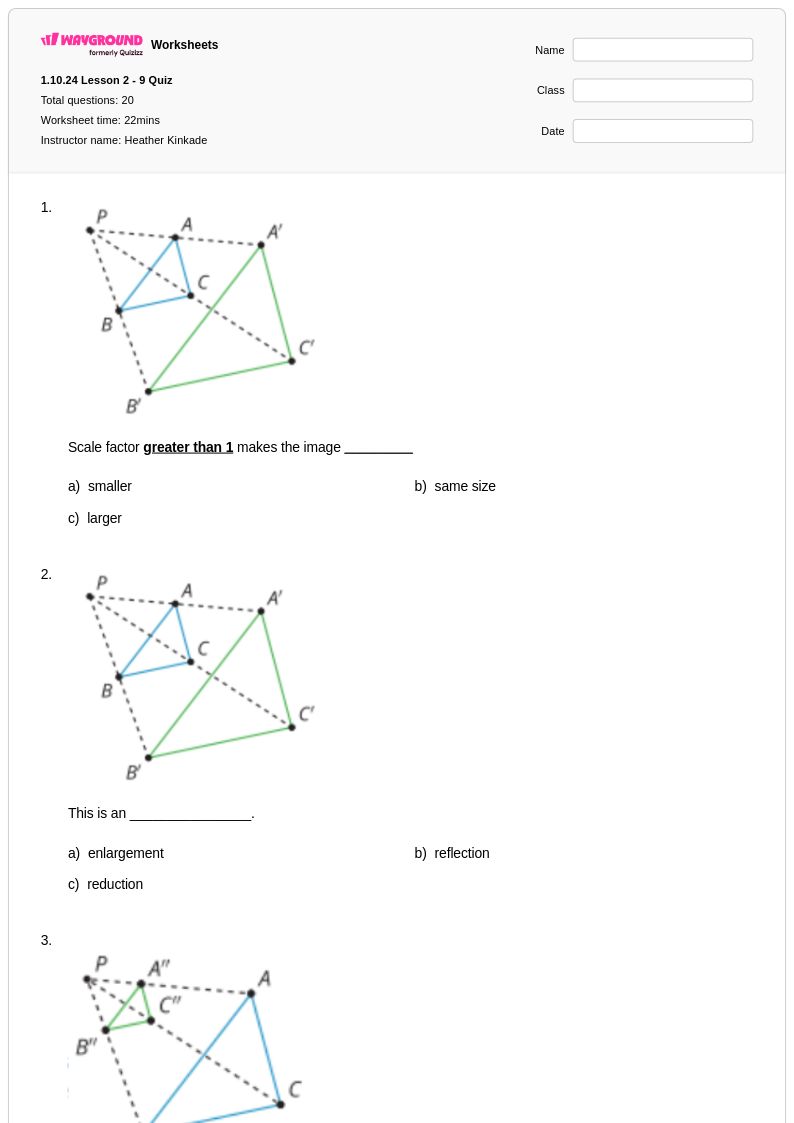
20 คิว
10th
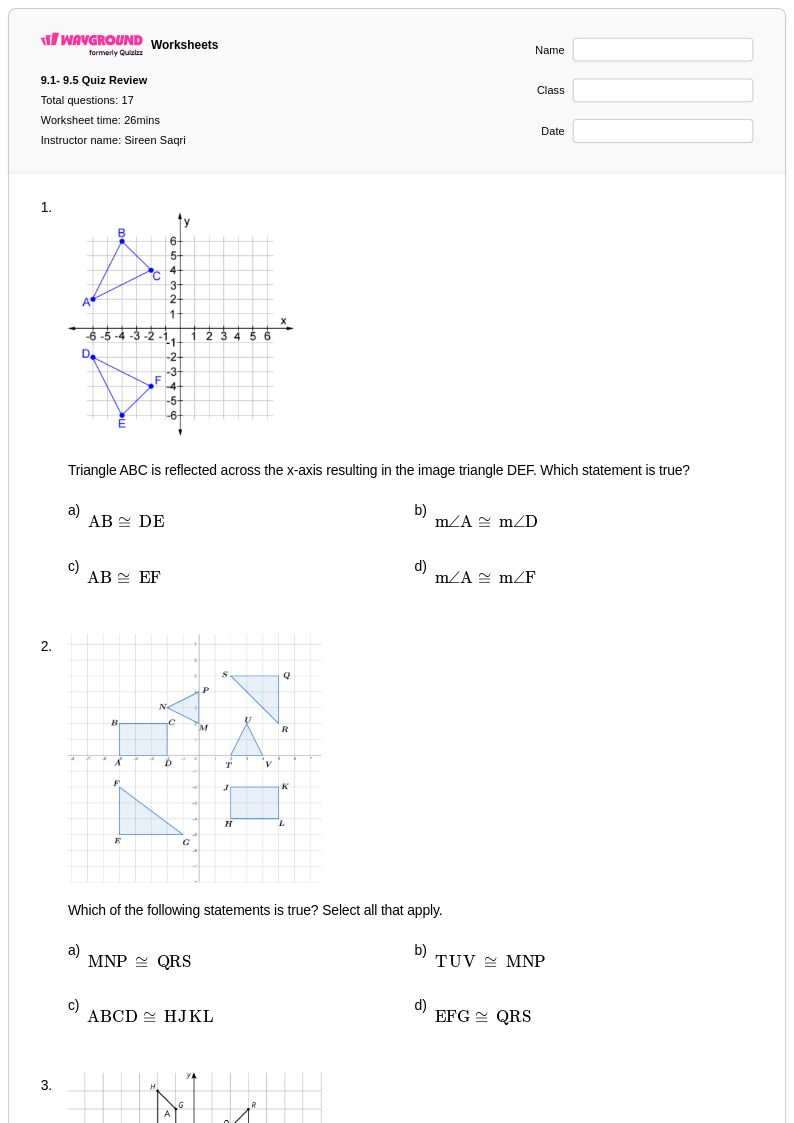
17 คิว
9th - 12th
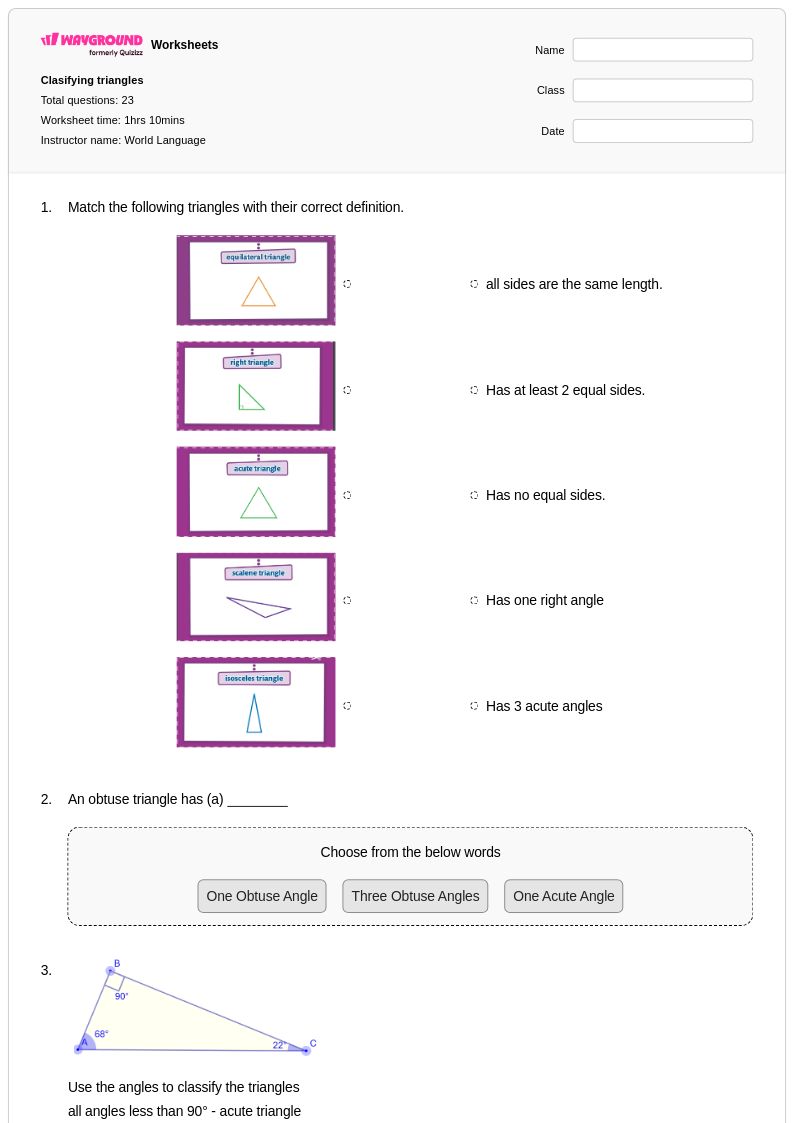
23 คิว
5th
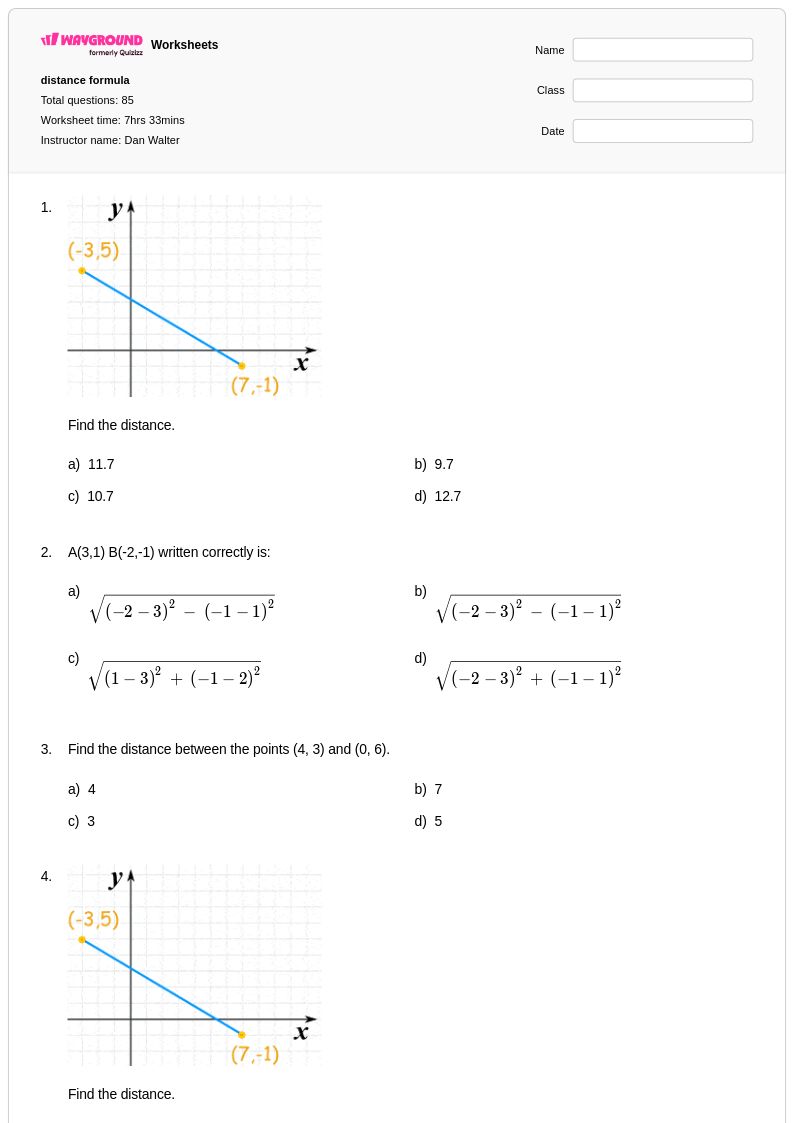
85 คิว
8th

14 คิว
9th
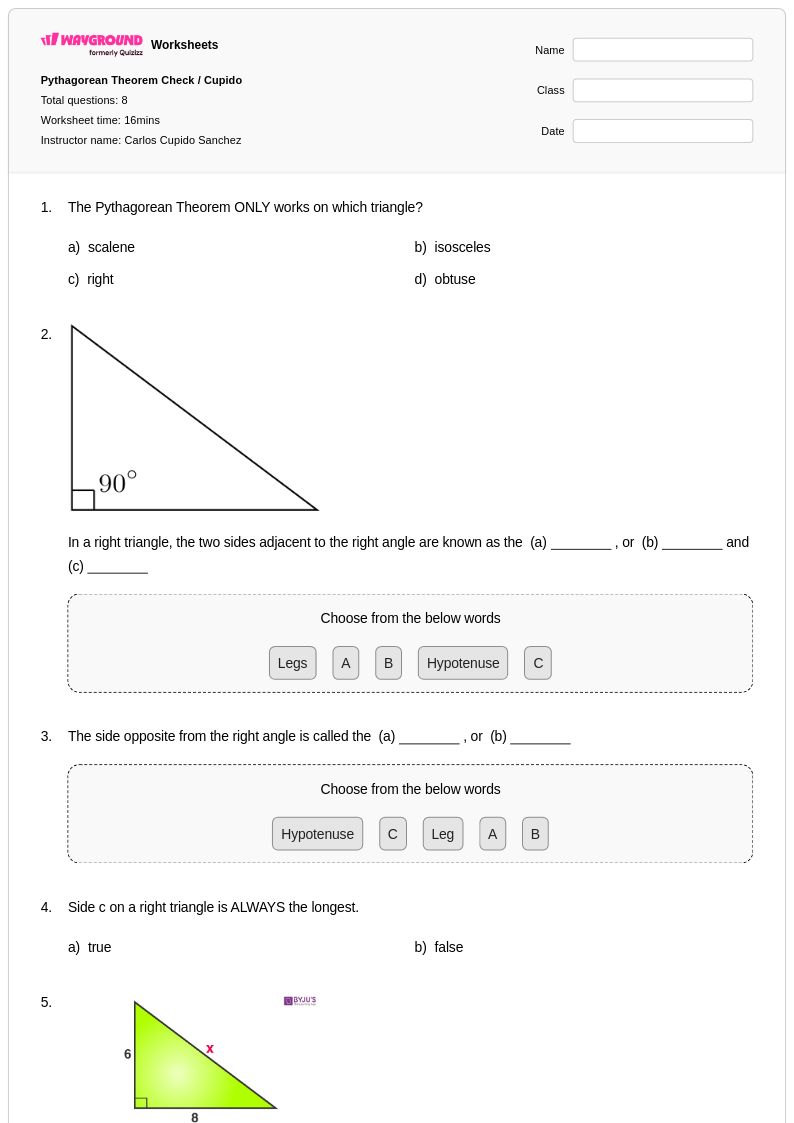
8 คิว
8th
23 คิว
8th
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน ทฤษฎีบทสามเหลี่ยมหน้าจั่ว ที่พิมพ์ได้
แบบฝึกหัดทฤษฎีบทสามเหลี่ยมหน้าจั่วจาก Wayground (เดิมคือ Quizizz) มอบโอกาสในการฝึกฝนอย่างครอบคลุมเพื่อให้นักเรียนเชี่ยวชาญหลักการพื้นฐานทางเรขาคณิตข้อหนึ่ง แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยให้นักเรียนเข้าใจว่ามุมฐานของสามเหลี่ยมหน้าจั่วมีขนาดเท่ากัน พร้อมทั้งพัฒนาทักษะที่จำเป็นในการวัดมุม การจำแนกประเภทสามเหลี่ยม และการสร้างบทพิสูจน์ทางเรขาคณิต ชุดแบบฝึกหัดประกอบด้วยโจทย์ฝึกฝนที่หลากหลาย ตั้งแต่การระบุมุมพื้นฐานไปจนถึงบทพิสูจน์หลายขั้นตอนที่ซับซ้อน โดยแต่ละแบบฝึกหัดมีเฉลยคำตอบโดยละเอียดเพื่อสนับสนุนการเรียนรู้ด้วยตนเองและการประเมินตนเอง นักเรียนจะได้ทำแบบฝึกหัดที่ดาวน์โหลดได้ฟรี ซึ่งจะช่วยเสริมสร้างการประยุกต์ใช้ทฤษฎีบทในบริบทของโลกแห่งความเป็นจริง สร้างความมั่นใจในการใช้เหตุผลทางเรขาคณิต พร้อมทั้งเสริมสร้างความสามารถในการจดจำและประยุกต์ใช้ความสัมพันธ์ที่สำคัญนี้ในสถานการณ์ทางคณิตศาสตร์ต่างๆ
Wayground (เดิมคือ Quizizz) ช่วยเสริมศักยภาพให้แก่ครูผู้สอนด้วยแหล่งข้อมูลทฤษฎีบทสามเหลี่ยมหน้าจั่วที่สร้างโดยครูหลายล้านรายการ ซึ่งช่วยลดความยุ่งยากในการวางแผนบทเรียนและยกระดับคุณภาพการสอน แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานทางคณิตศาสตร์เฉพาะได้อย่างรวดเร็ว ในขณะที่เครื่องมือการปรับระดับความยากง่ายช่วยให้สามารถปรับแต่งได้อย่างราบรื่นเพื่อตอบสนองความต้องการในการเรียนรู้และระดับความสามารถที่หลากหลาย ชุดแบบฝึกหัดที่ครอบคลุมเหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่สามารถพิมพ์ได้และเวอร์ชันดิจิทัลแบบโต้ตอบได้ ทำให้มีความยืดหยุ่นสำหรับการสอนในห้องเรียน การบ้าน และการเตรียมการประเมิน ครูสามารถใช้ทรัพยากรที่หลากหลายเหล่านี้สำหรับการฝึกฝนทักษะเฉพาะด้าน การสนับสนุนการแก้ไขปัญหาสำหรับผู้เรียนที่ประสบปัญหา และโอกาสในการเสริมสร้างความรู้สำหรับนักเรียนที่มีความสามารถสูง เพื่อให้มั่นใจว่าผู้เรียนทุกคนสามารถพัฒนาความเชี่ยวชาญในแนวคิดทางเรขาคณิตที่สำคัญนี้ได้ผ่านประสบการณ์ทางคณิตศาสตร์ที่ท้าทายและน่าสนใจอย่างเหมาะสม
