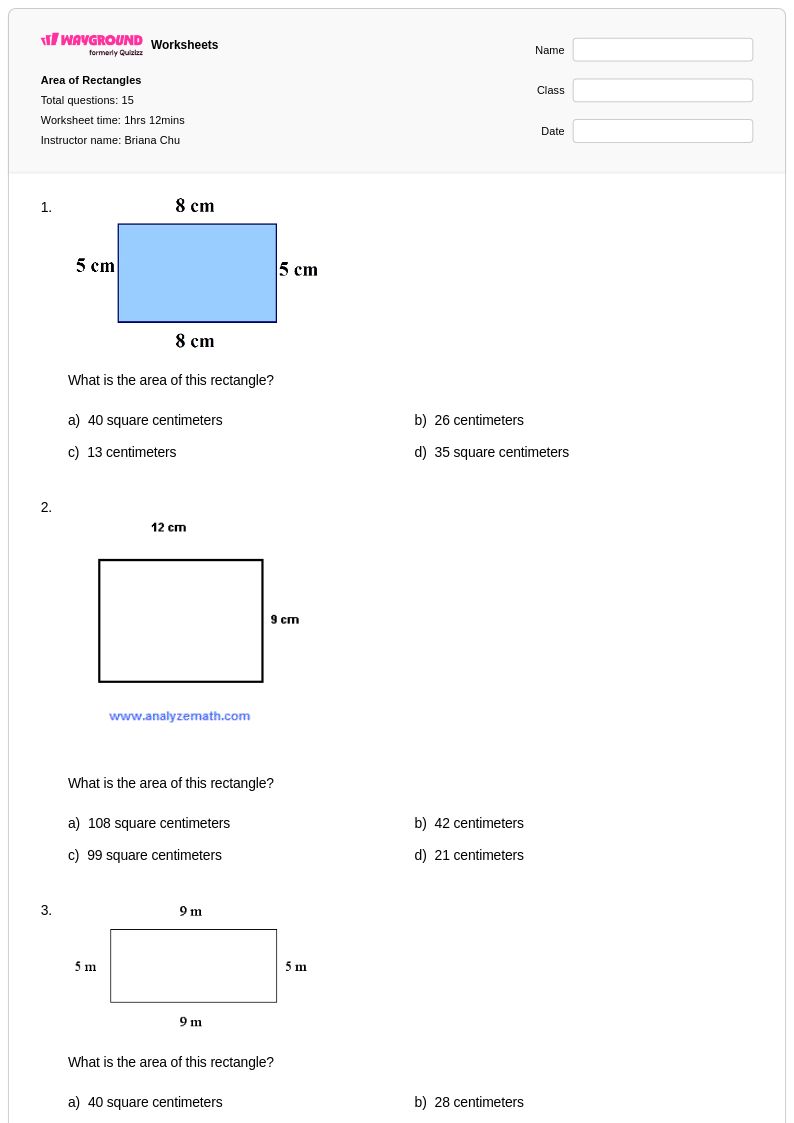
15 คิว
3rd - 5th
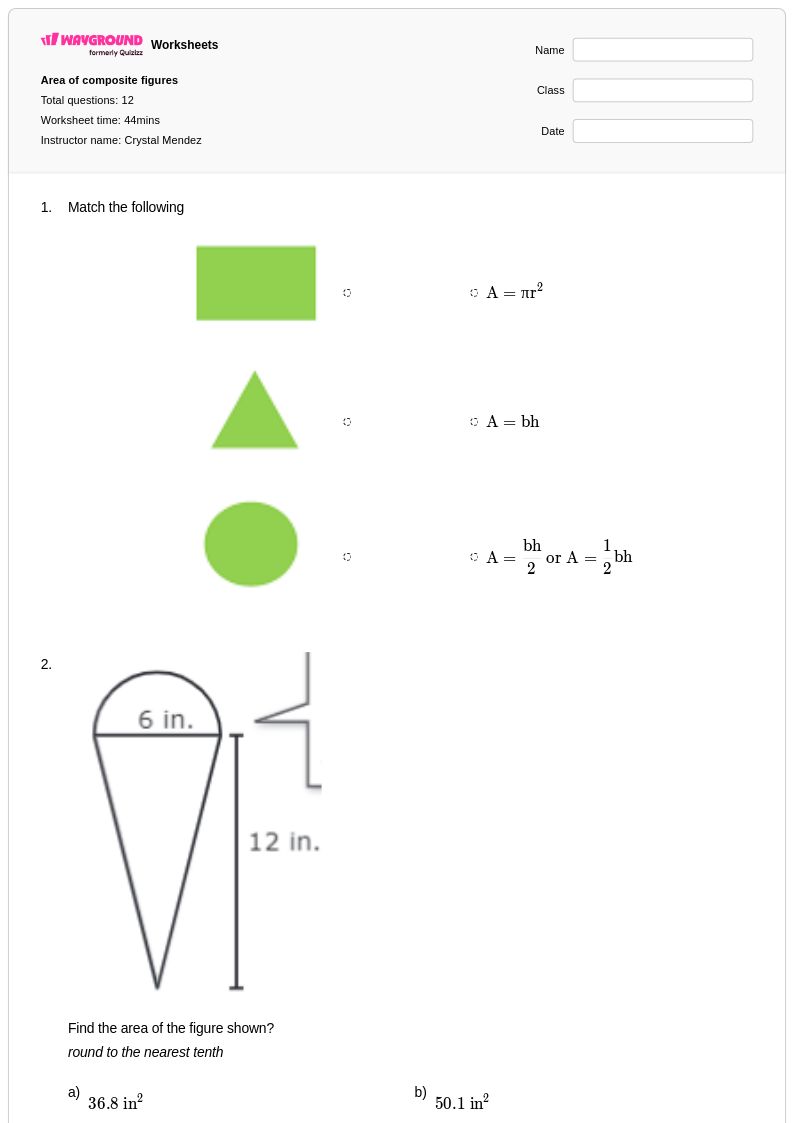
12 คิว
10th

10 คิว
6th

10 คิว
6th - Uni
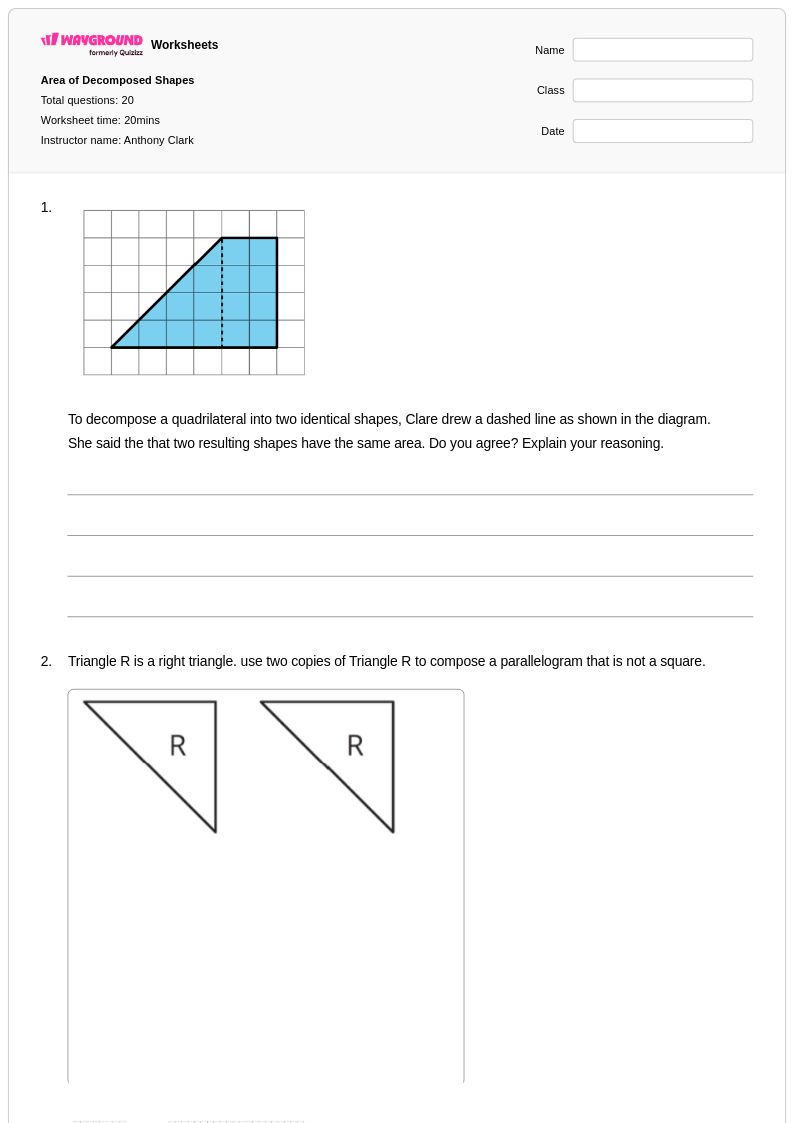
20 คิว
6th - Uni

15 คิว
11th
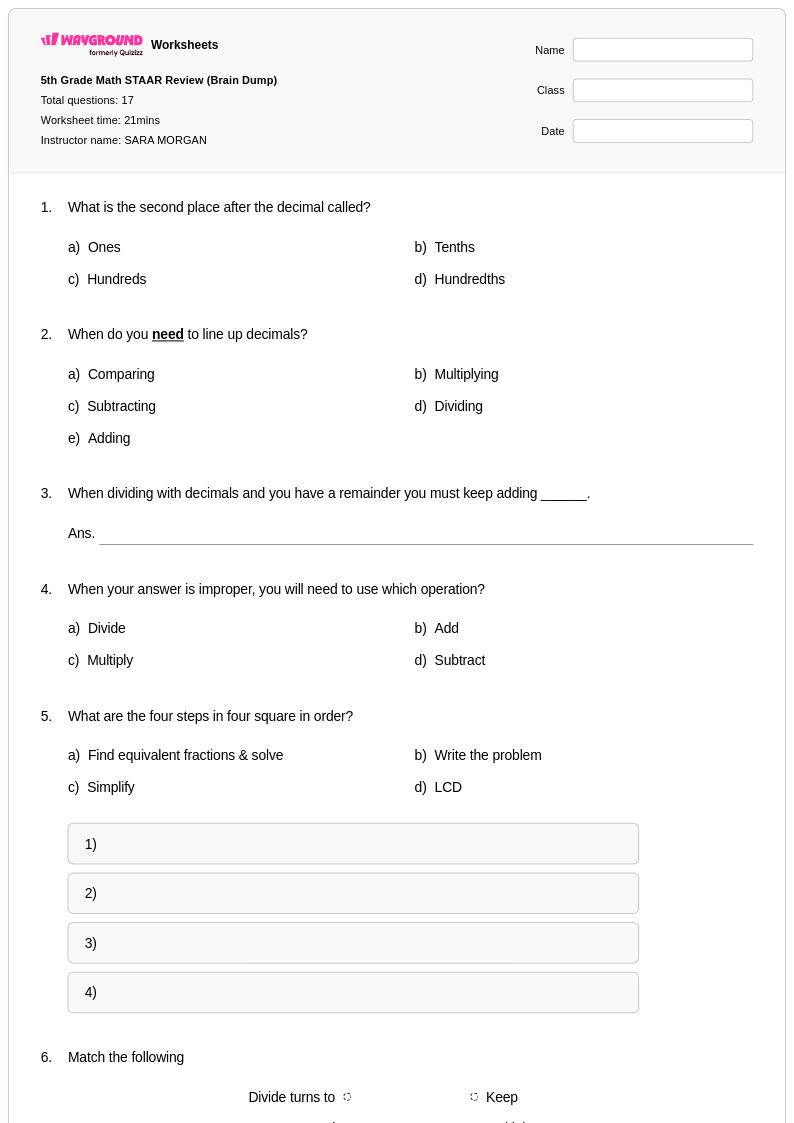
17 คิว
5th
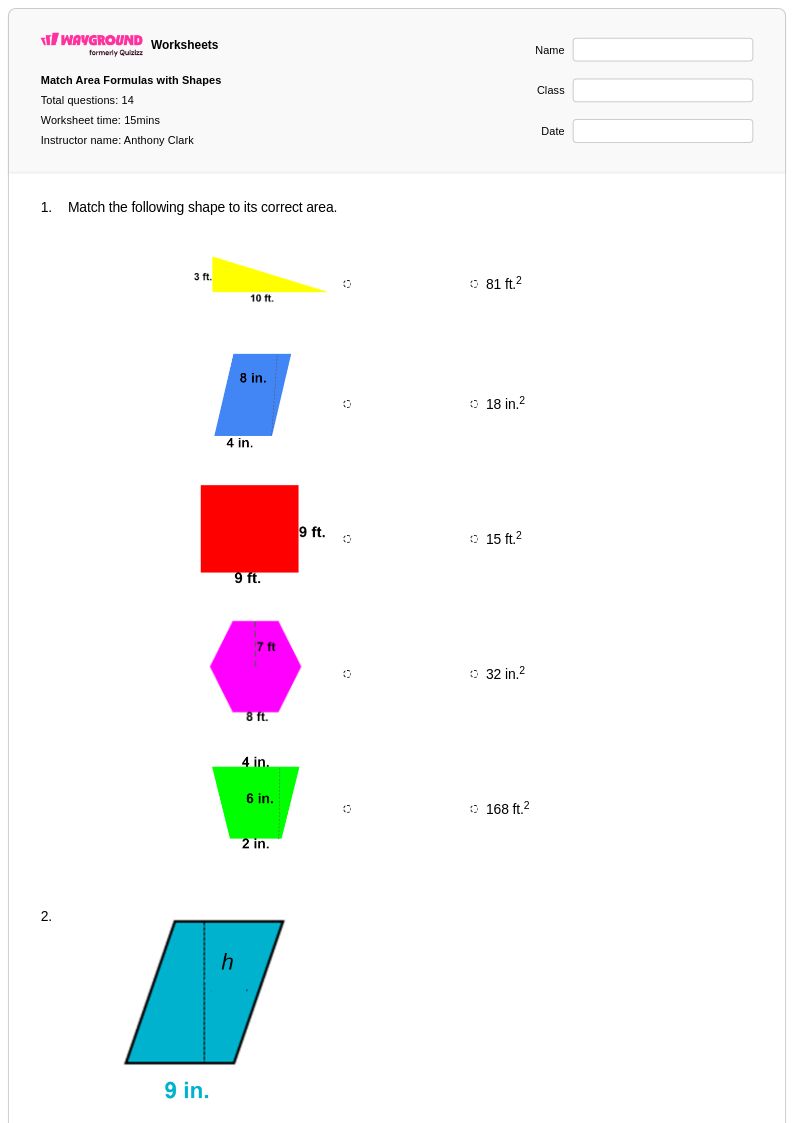
15 คิว
6th - Uni

12 คิว
6th

20 คิว
7th

10 คิว
5th - Uni
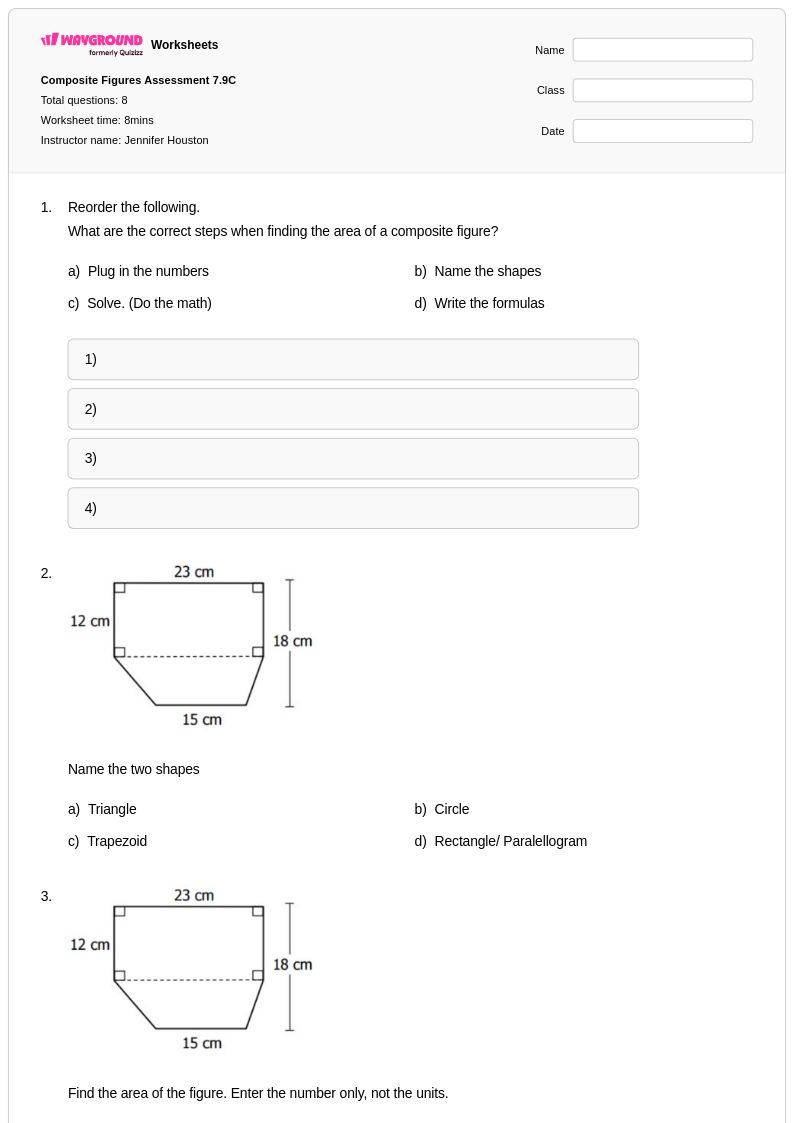
8 คิว
7th
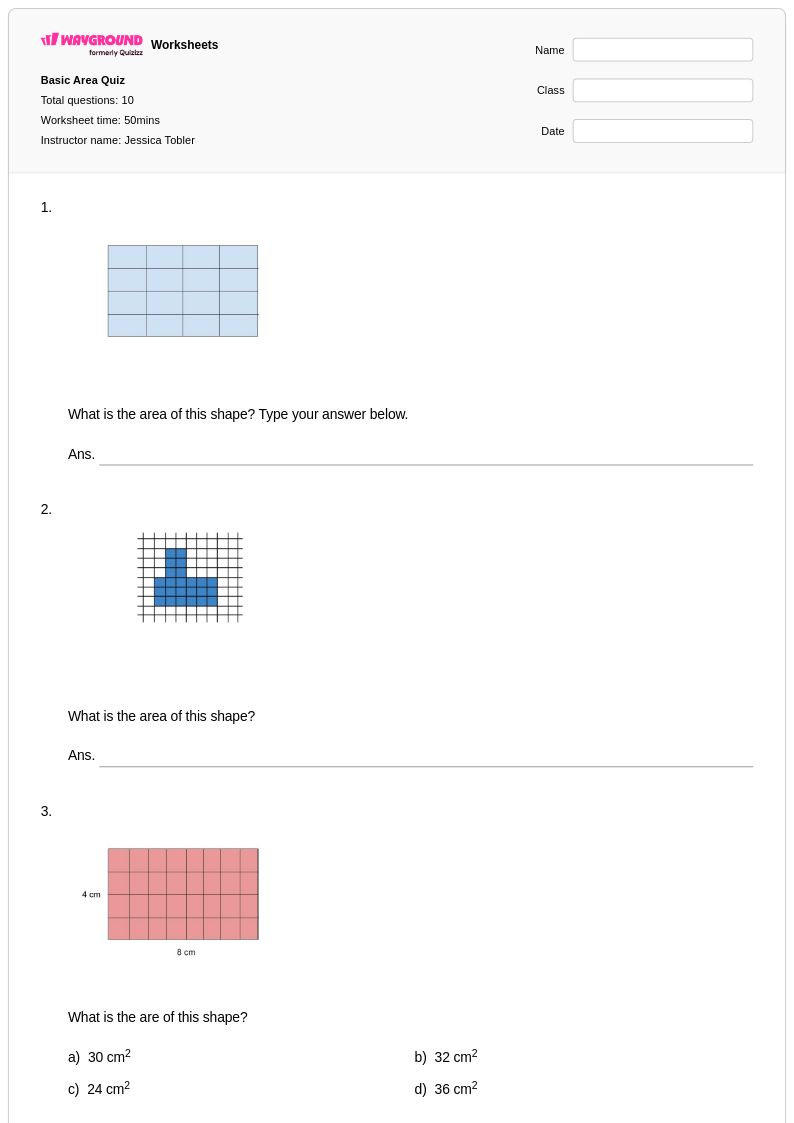
10 คิว
3rd
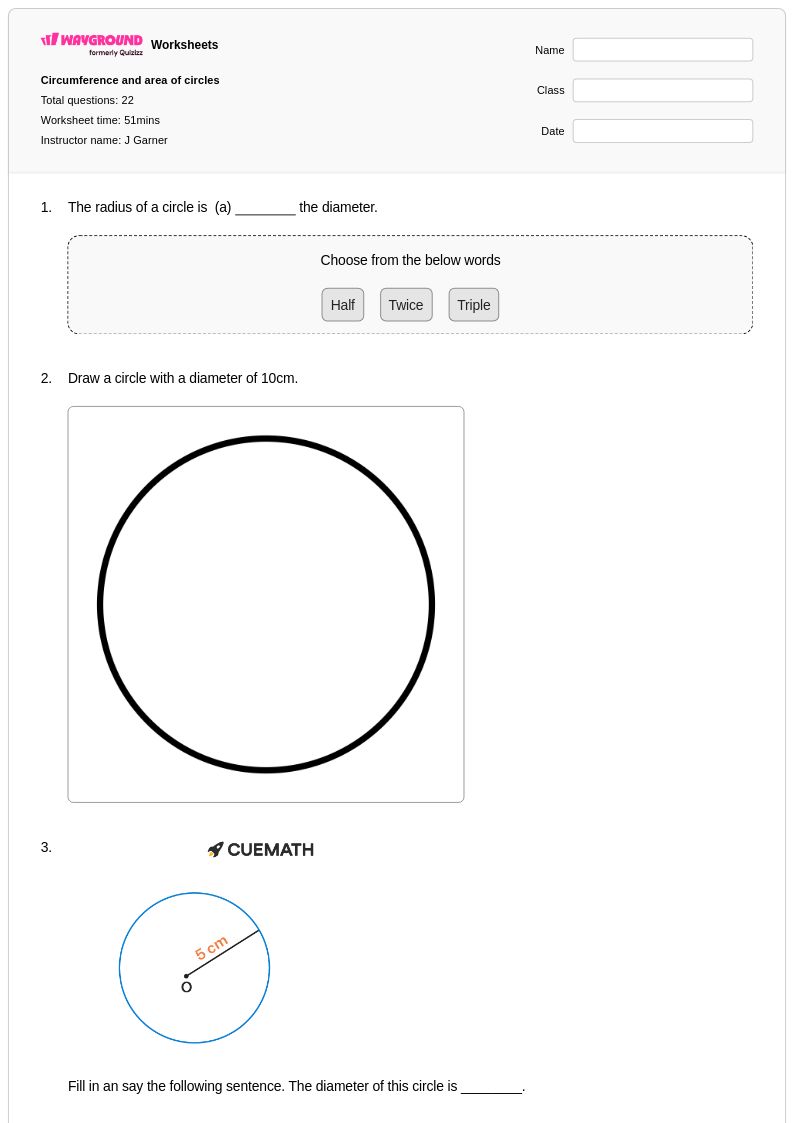
22 คิว
7th

10 คิว
6th

10 คิว
4th
15 คิว
5th

13 คิว
6th
13 คิว
8th
9 คิว
6th
10 คิว
6th

14 คิว
6th

21 คิว
4th
7 คิว
7th
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน พื้นที่ของรูปทรงสี่เหลี่ยมผืนผ้า ที่พิมพ์ได้
แบบฝึกหัดเรื่องพื้นที่ของรูปทรงเรขาคณิตแบบเส้นตรงจาก Wayground (เดิมคือ Quizizz) มีแบบฝึกหัดที่ครอบคลุม ออกแบบมาเพื่อช่วยให้นักเรียนเชี่ยวชาญการคำนวณพื้นที่ของรูปทรงเรขาคณิตที่ซับซ้อนซึ่งประกอบด้วยสี่เหลี่ยมผืนผ้าและสี่เหลี่ยมจัตุรัส แหล่งข้อมูลที่สร้างขึ้นอย่างเชี่ยวชาญเหล่านี้ช่วยเสริมสร้างทักษะทางคณิตศาสตร์ที่สำคัญ รวมถึงการแยกส่วนรูปทรง การประยุกต์ใช้สูตรพื้นที่ และการให้เหตุผลเชิงพื้นที่ ผ่านแบบฝึกหัดที่เป็นระบบซึ่งค่อยๆ พัฒนาจากรูปทรงตัว L พื้นฐานไปจนถึงรูปทรงเรขาคณิตแบบเส้นตรงที่ซับซ้อนมากขึ้น แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดและวิธีแก้ปัญหาทีละขั้นตอน ช่วยให้นักเรียนตรวจสอบงานของตนเองและเข้าใจกลยุทธ์การแก้ปัญหา แบบฝึกหัดเหล่านี้มีให้ใช้งานฟรีในรูปแบบ PDF ที่สะดวก สนับสนุนทั้งการเรียนการสอนในห้องเรียนและการเรียนรู้ด้วยตนเอง ในขณะเดียวกันก็สร้างความมั่นใจในแนวคิดการวัดทางเรขาคณิต
Wayground (เดิมคือ Quizizz) ช่วยให้ครูผู้สอนเข้าถึงแหล่งข้อมูลนับล้านที่สร้างโดยครูผู้สอนโดยเฉพาะ ซึ่งเน้นเรื่องพื้นที่ของรูปทรงเรขาคณิตแบบเส้นตรง มีคุณสมบัติการค้นหาและการกรองที่มีประสิทธิภาพ ช่วยให้ครูผู้สอนสามารถค้นหาสื่อที่สอดคล้องกับมาตรฐานหลักสูตรและความต้องการของนักเรียนได้อย่างสมบูรณ์แบบ เครื่องมือปรับระดับความยากง่ายของแพลตฟอร์มช่วยให้ครูสามารถปรับแต่งแบบฝึกหัดให้เหมาะสมกับระดับทักษะต่างๆ ได้ ในขณะที่ตัวเลือกการจัดรูปแบบที่ยืดหยุ่นช่วยให้สามารถสร้างทั้งไฟล์ PDF ที่พิมพ์ได้สำหรับการใช้งานในห้องเรียนแบบดั้งเดิม และรูปแบบดิจิทัลสำหรับสภาพแวดล้อมการเรียนรู้แบบโต้ตอบ คุณสมบัติที่ครอบคลุมเหล่านี้ช่วยให้การวางแผนบทเรียนง่ายขึ้น โดยนำเสนอสื่อการเรียนรู้ที่พร้อมใช้งานสำหรับการฝึกฝนทักษะ การแก้ไขปัญหาเฉพาะจุดสำหรับผู้เรียนที่มีปัญหา และกิจกรรมเสริมสำหรับนักเรียนที่มีความสามารถสูง ทำให้มั่นใจได้ว่าครูผู้สอนทุกคนสามารถตอบสนองความต้องการการเรียนรู้ที่หลากหลายได้อย่างมีประสิทธิภาพ ในขณะที่ยังคงมุ่งเน้นไปที่แนวคิดเรื่องพื้นที่ทางเรขาคณิตอย่างสม่ำเสมอ
