หัวข้อแนะนำสำหรับคุณ
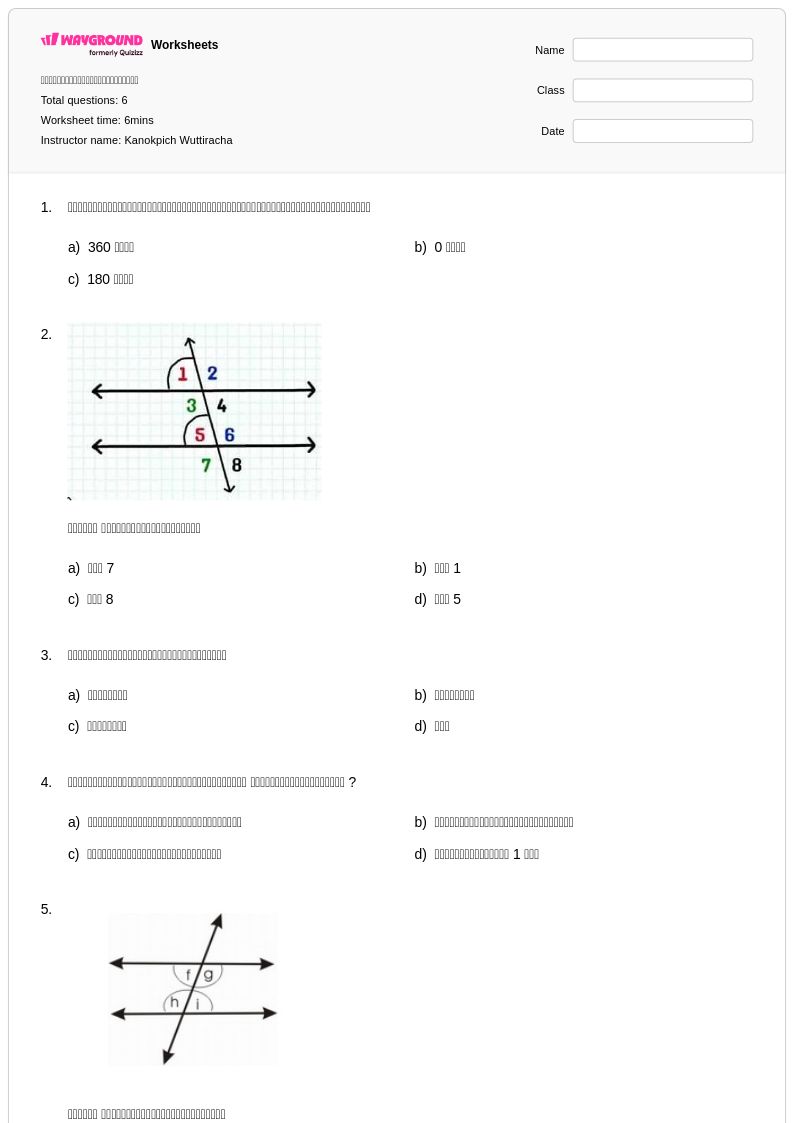
6 คิว
Uni

15 คิว

10 คิว
9th
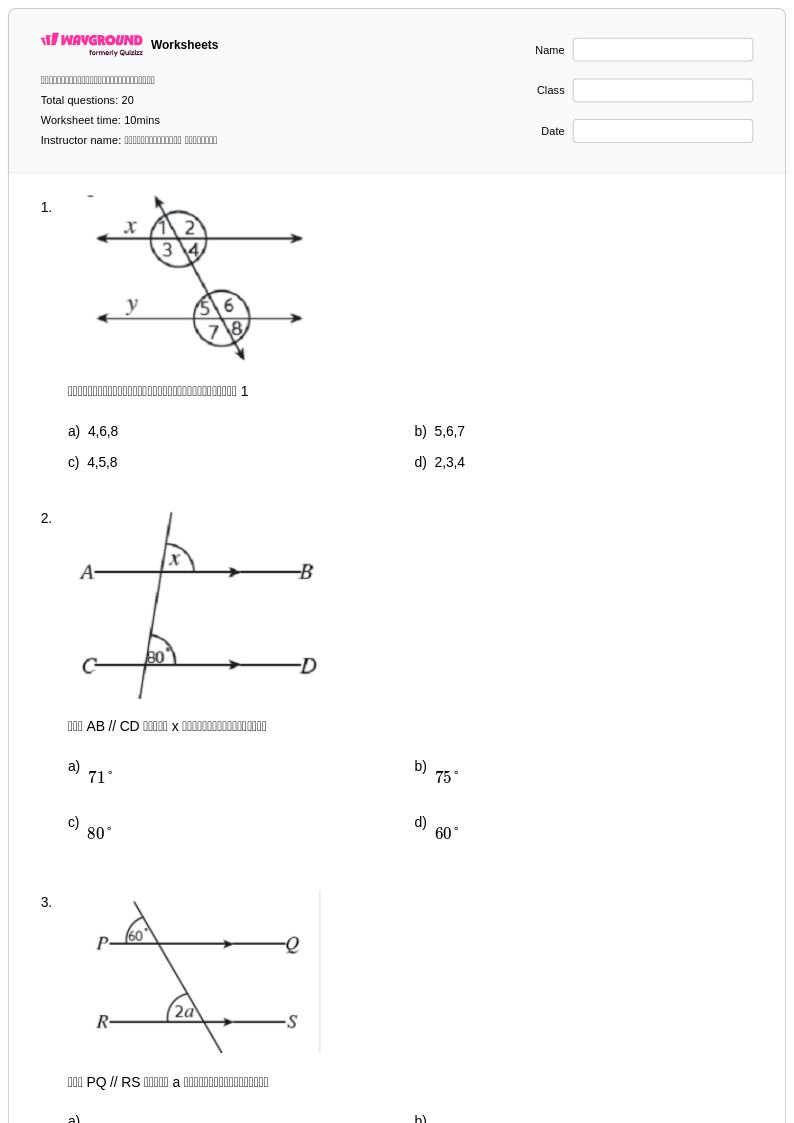
20 คิว
8th

17 คิว
9th

19 คิว
7th
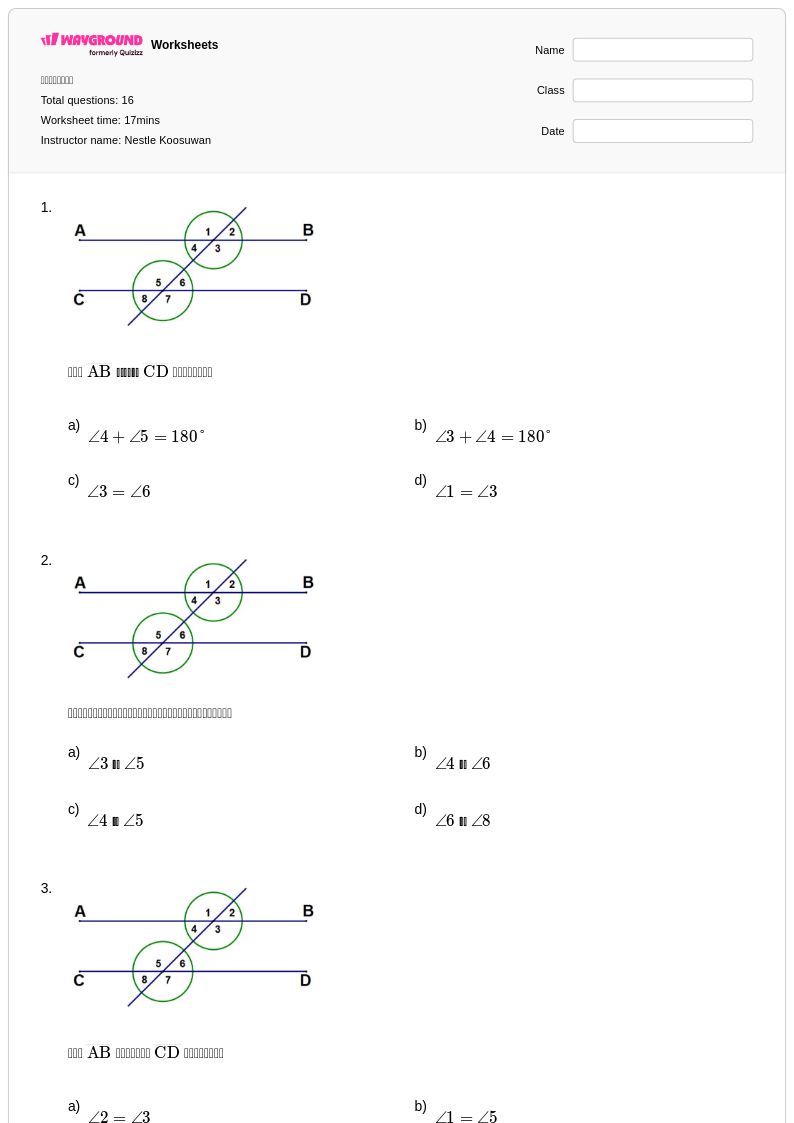
16 คิว
6th - 8th
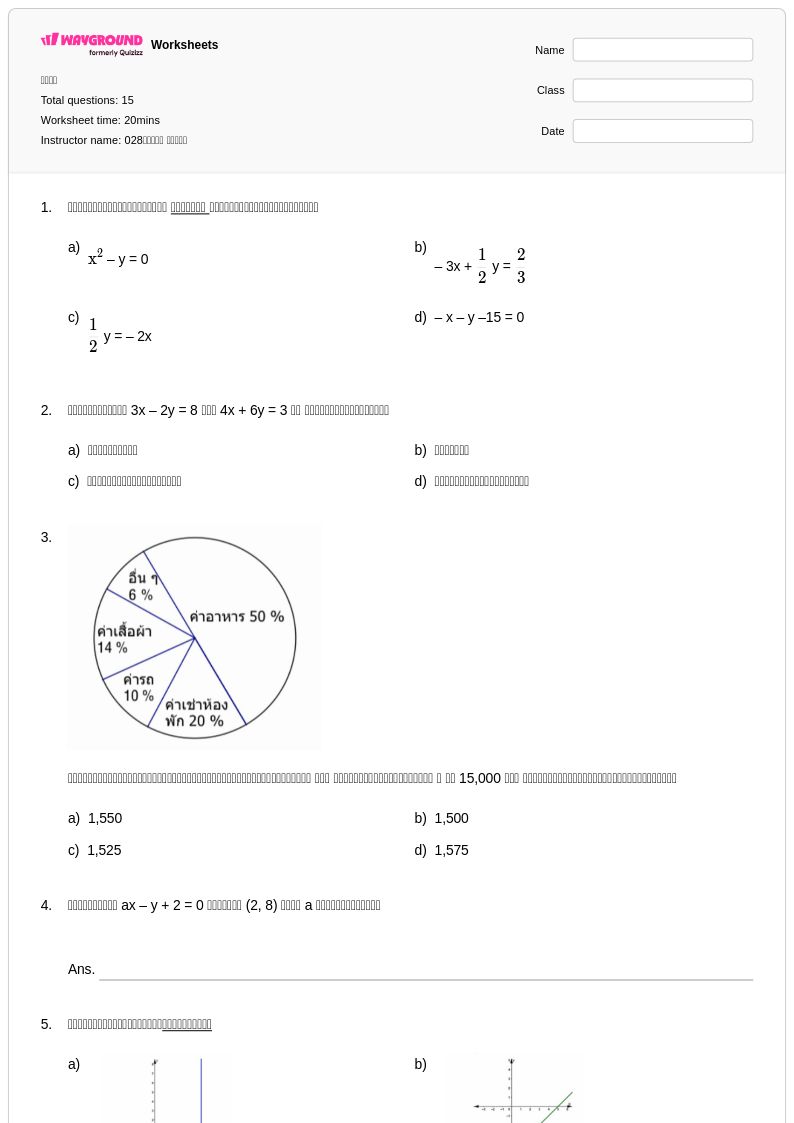
15 คิว
9th - 12th
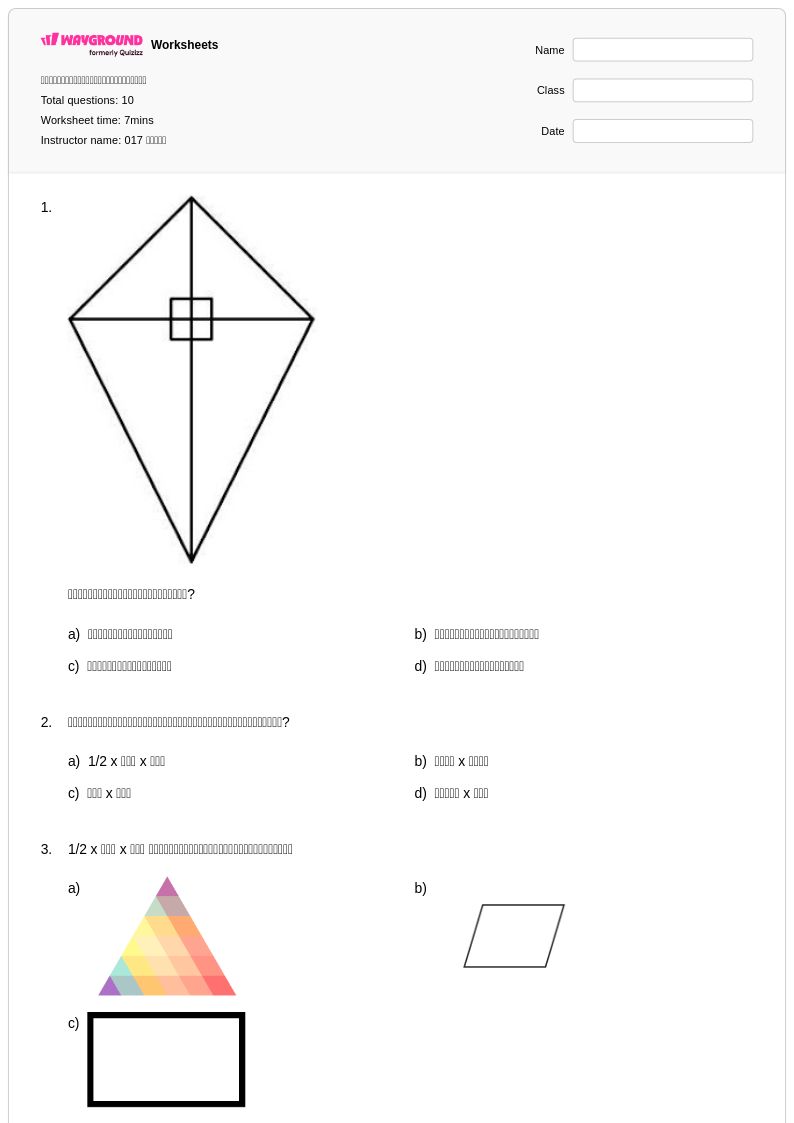
10 คิว
4th - 5th

10 คิว
9th
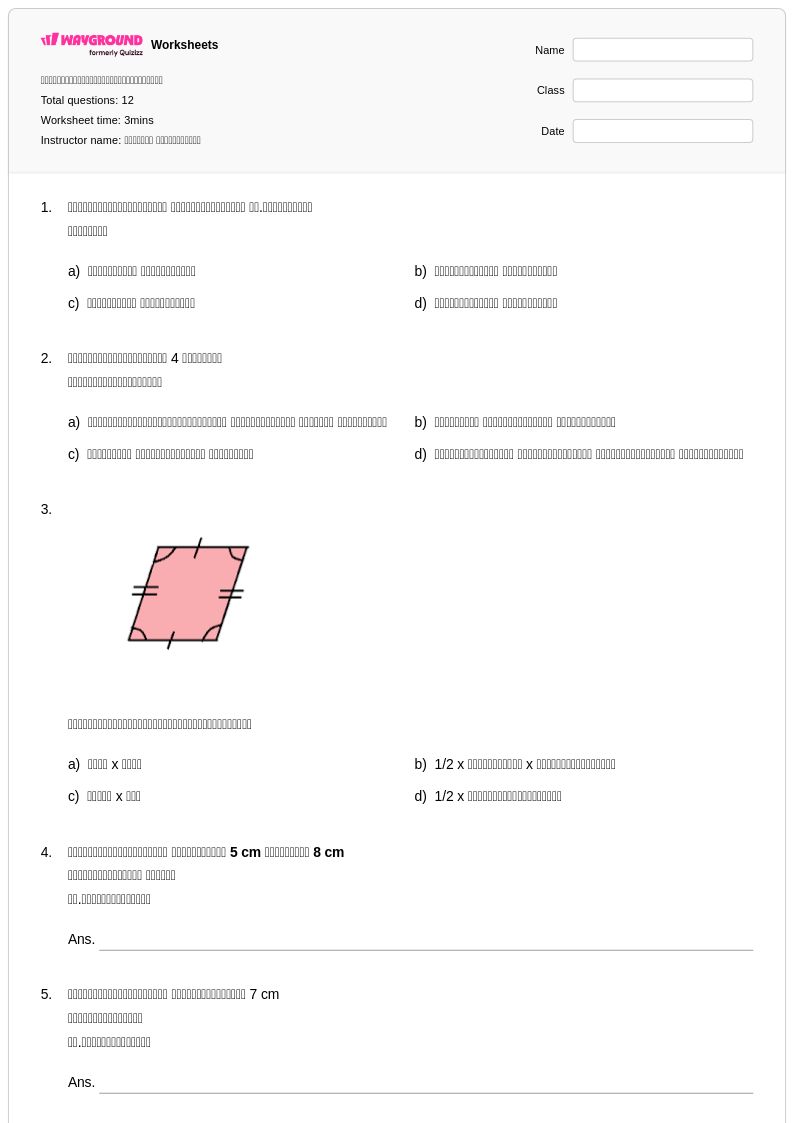
12 คิว
9th
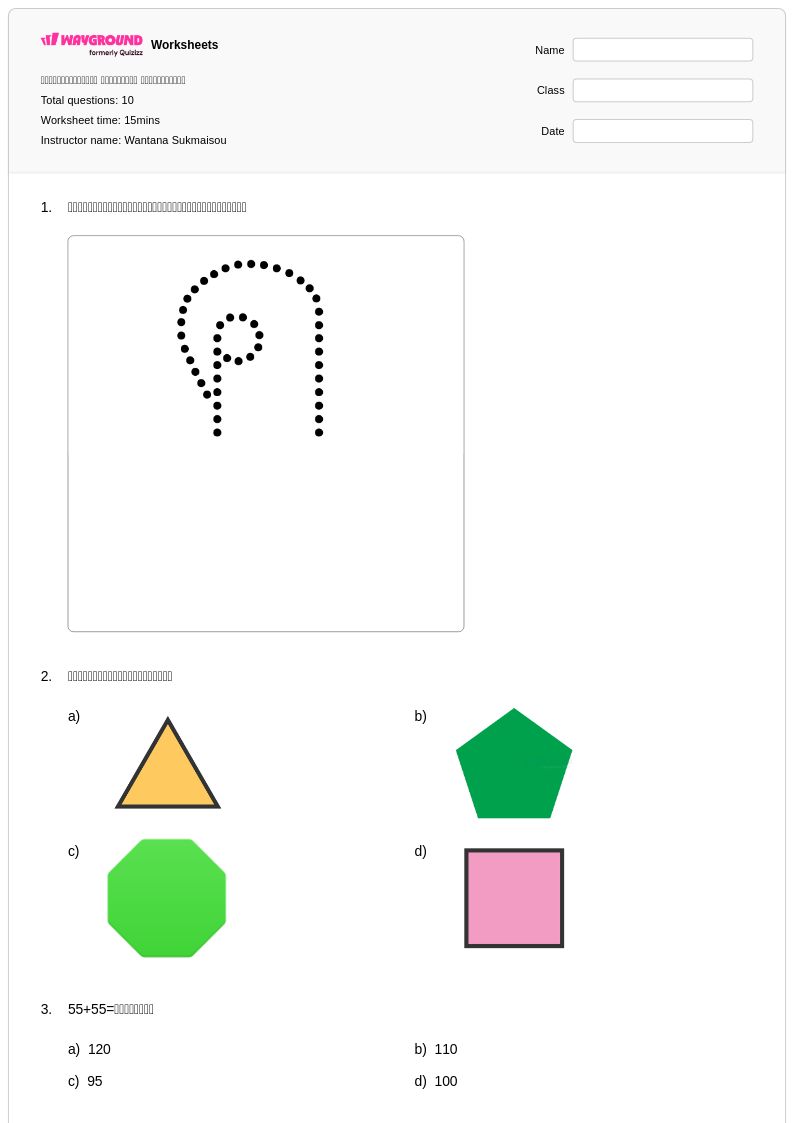
10 คิว
6th

20 คิว
9th

37 คิว
3rd

20 คิว
2nd

10 คิว
4th - 6th
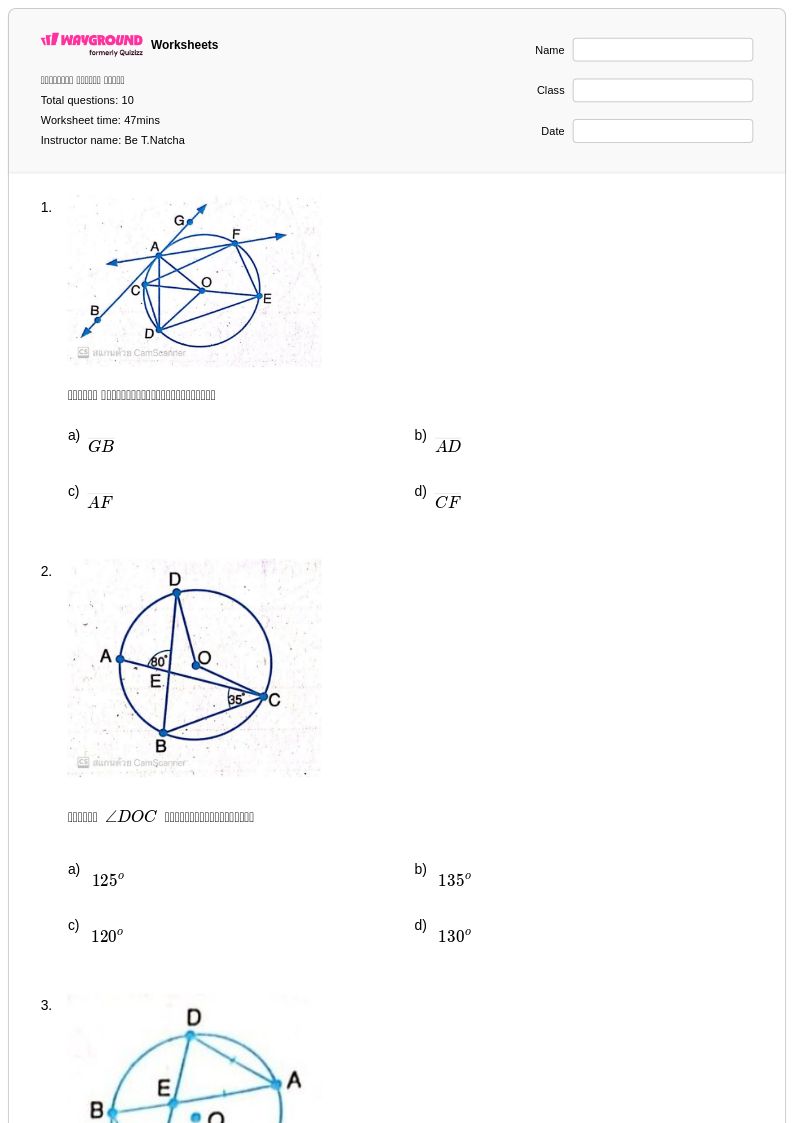
10 คิว
7th - 9th

20 คิว
Uni - PD

10 คิว
PD

10 คิว
11th

10 คิว
11th

10 คิว
11th

15 คิว

15 คิว
7th
สำรวจแผ่นงาน เส้น ตามหัวข้อ
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน เส้น ที่พิมพ์ได้
แบบฝึกหัดเรื่องเส้นตรงจาก Wayground (เดิมคือ Quizizz) เป็นแบบฝึกหัดที่ครอบคลุมสำหรับนักเรียนที่ต้องการพัฒนาแนวคิดทางเรขาคณิตพื้นฐานและทักษะการคิดเชิงพื้นที่ แหล่งข้อมูลทางคณิตศาสตร์เหล่านี้เน้นคุณสมบัติที่สำคัญของเส้นตรง เช่น เส้นขนาน เส้นตั้งฉาก และเส้นตัดกัน รวมถึงความสัมพันธ์ของมุมที่เกิดขึ้นเมื่อเส้นตรงมีปฏิสัมพันธ์กัน นักเรียนจะได้ทำแบบฝึกหัดที่มีโครงสร้างอย่างรอบคอบ ซึ่งช่วยสร้างความเข้าใจเกี่ยวกับส่วนของเส้นตรง รังสี และเส้นตรงอนันต์ พร้อมทั้งพัฒนาความชำนาญในการวัด การวาด และการระบุรูปแบบของเส้นตรงต่างๆ แบบฝึกหัดมีเฉลยคำตอบโดยละเอียดและสามารถดาวน์โหลดได้ฟรีในรูปแบบ PDF ที่สะดวก ช่วยให้นักเรียนสามารถเชี่ยวชาญหลักการทางเรขาคณิตหลักผ่านแบบฝึกหัดสร้างทักษะอย่างเป็นระบบ ซึ่งเสริมการเรียนการสอนในห้องเรียน
Wayground (เดิมคือ Quizizz) ช่วยให้ครูผู้สอนมีแหล่งข้อมูลเรขาคณิตเส้นตรงที่สร้างโดยครูผู้สอนนับล้านรายการ ออกแบบมาเพื่อรองรับความต้องการการเรียนรู้และเป้าหมายการสอนที่หลากหลาย ความสามารถในการค้นหาและกรองข้อมูลที่แข็งแกร่งของแพลตฟอร์มช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานคณิตศาสตร์เฉพาะได้อย่างรวดเร็ว ในขณะที่เครื่องมือการแบ่งระดับช่วยให้สามารถปรับแต่งให้เหมาะกับระดับทักษะและรูปแบบการเรียนรู้ต่างๆ ได้ สื่อการสอนเรขาคณิตเหล่านี้มีให้เลือกทั้งแบบพิมพ์ได้และแบบดิจิทัล รวมถึงไฟล์ PDF ที่ดาวน์โหลดได้ ทำให้สามารถปรับใช้ได้ทั้งในห้องเรียน การบ้าน หรือการเรียนรู้ทางไกล ครูสามารถใช้ชุดแบบฝึกหัดที่ครอบคลุมเหล่านี้เพื่อฝึกฝนทักษะเฉพาะด้าน สนับสนุนการแก้ไขปัญหา และกิจกรรมเสริมความรู้ เพื่อให้มั่นใจว่านักเรียนทุกคนพัฒนาความเข้าใจพื้นฐานที่แข็งแกร่งเกี่ยวกับความสัมพันธ์ของเส้นและการให้เหตุผลทางเรขาคณิต ซึ่งจำเป็นต่อความสำเร็จในวิชาคณิตศาสตร์ขั้นสูง
