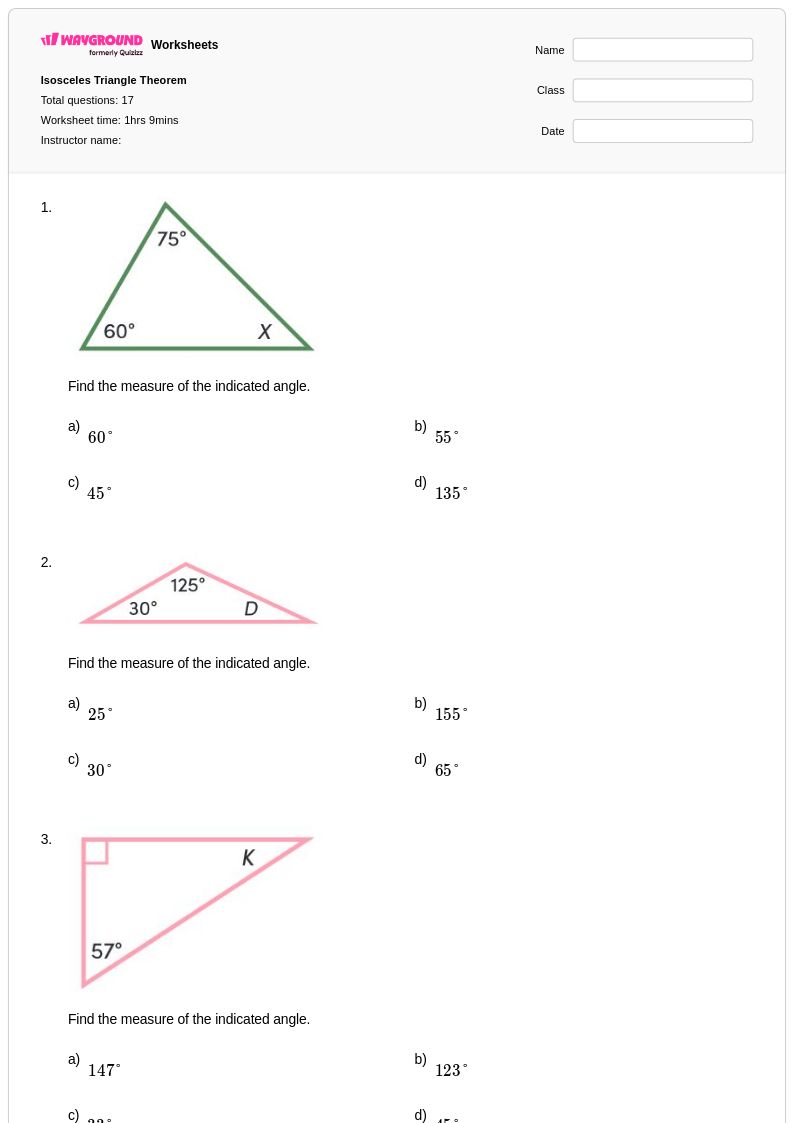
17Q
8th - 10th
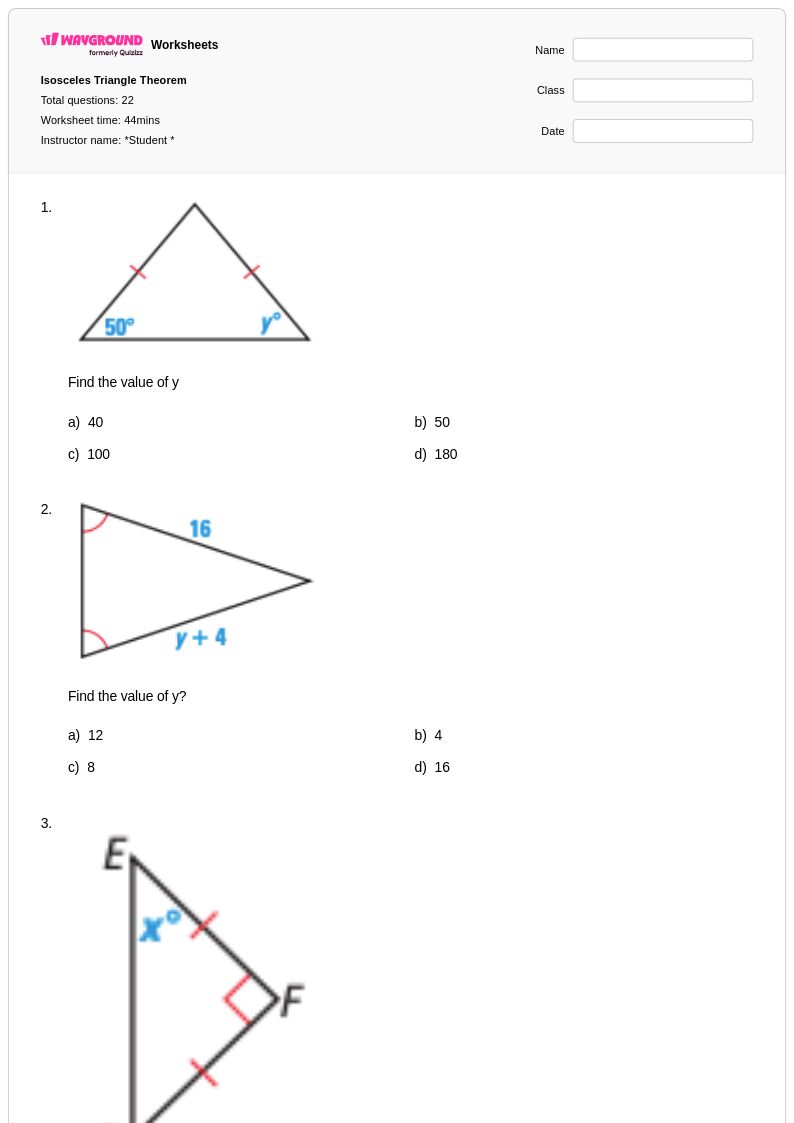
22Q
9th - 10th
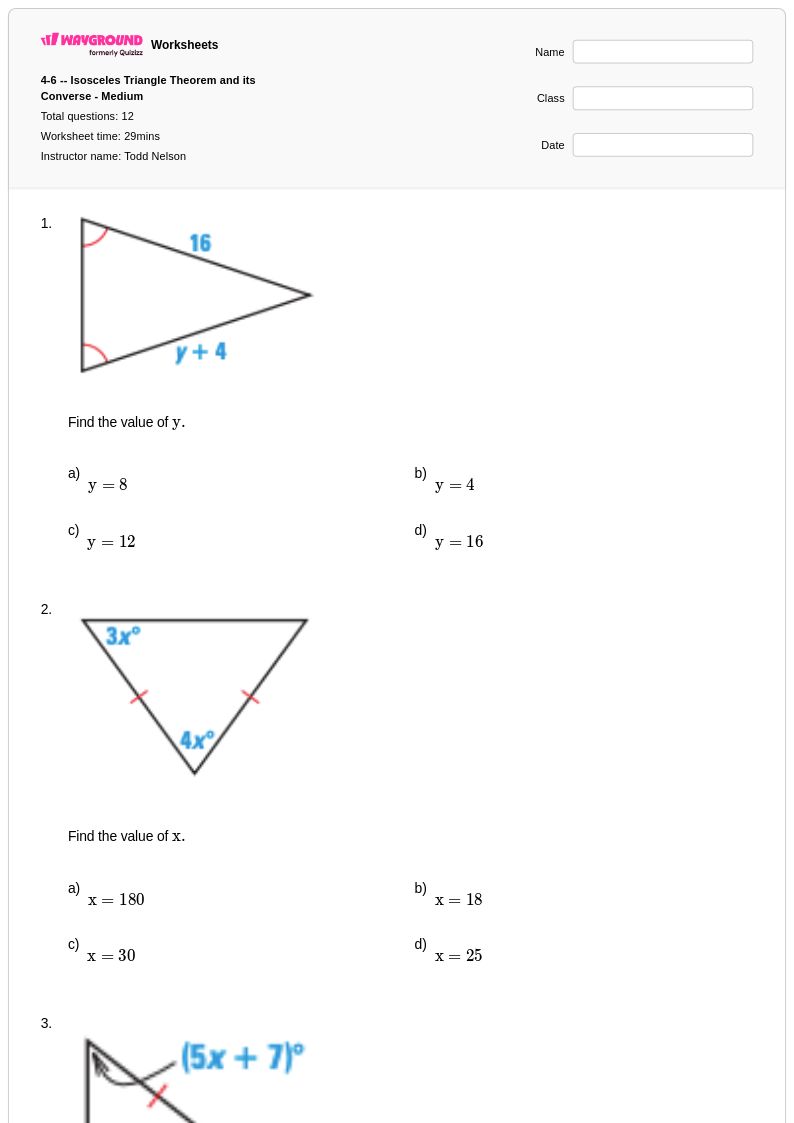
12Q
10th
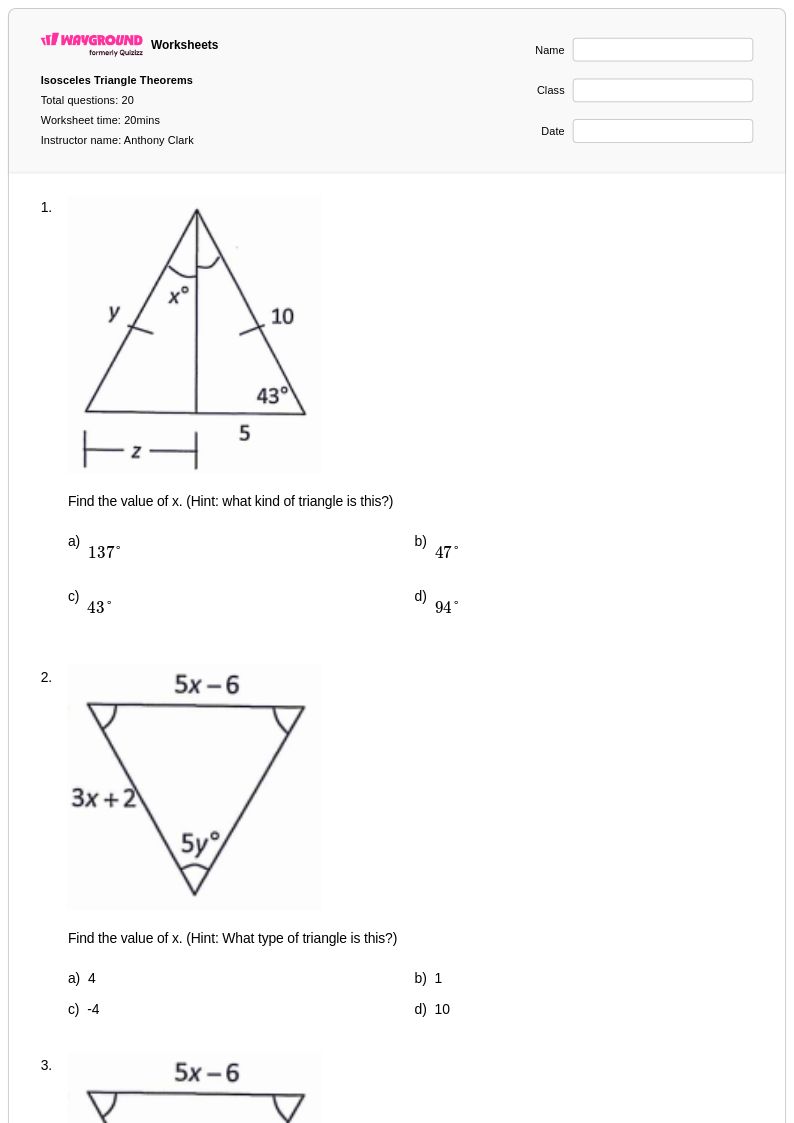
20Q
10th - Uni

8Q
KG
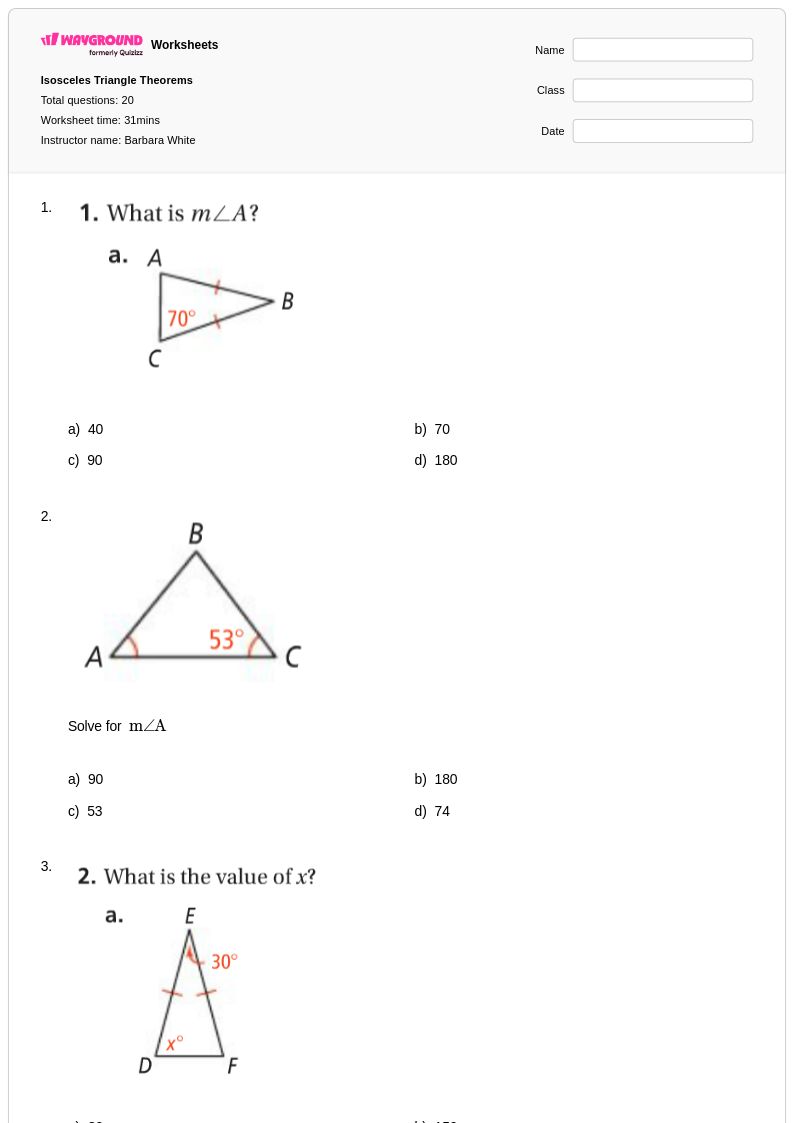
20Q
9th - 10th

13Q
9th - 10th
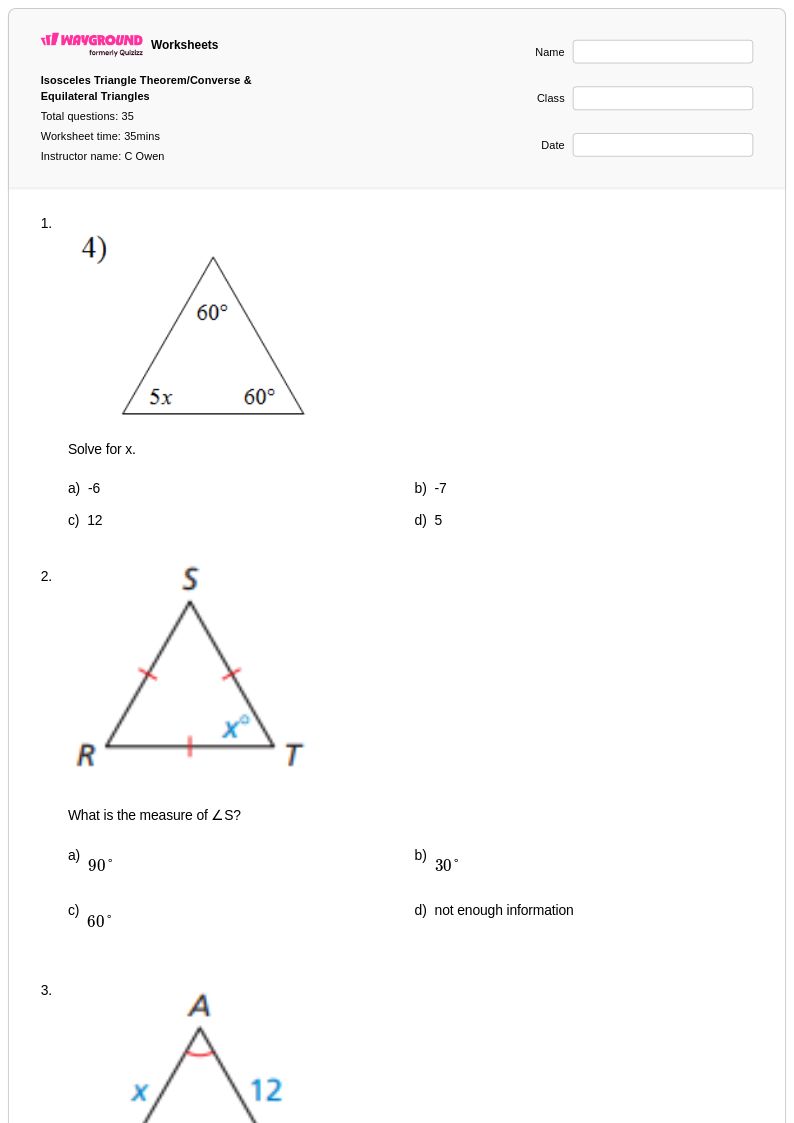
35Q
10th

14Q
10th

11Q
8th - 12th
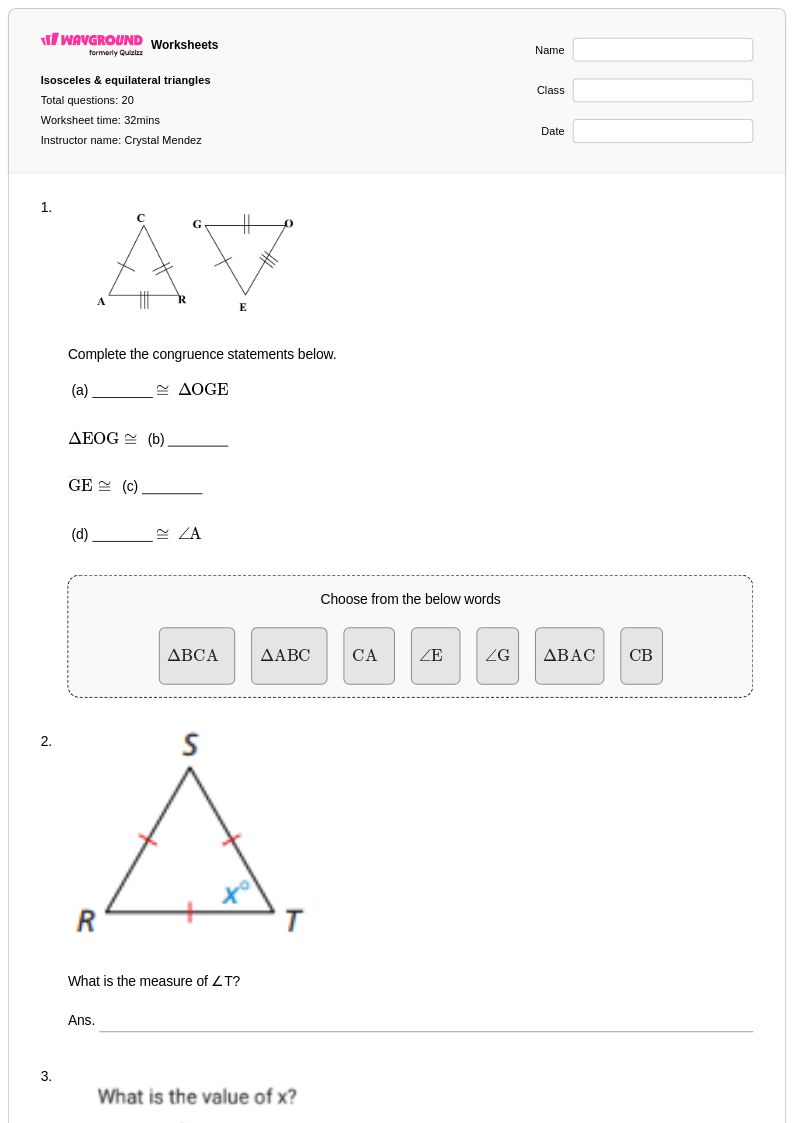
20Q
10th

20Q
9th - 12th

30Q
10th
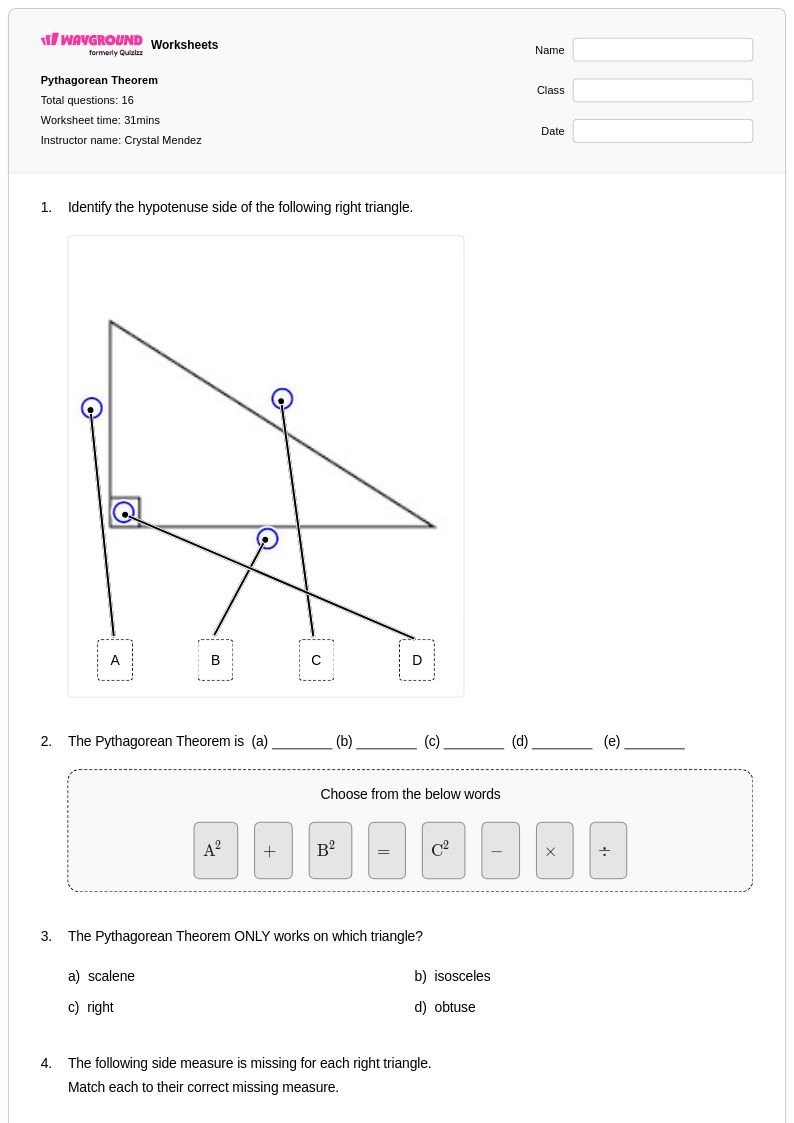
16Q
10th
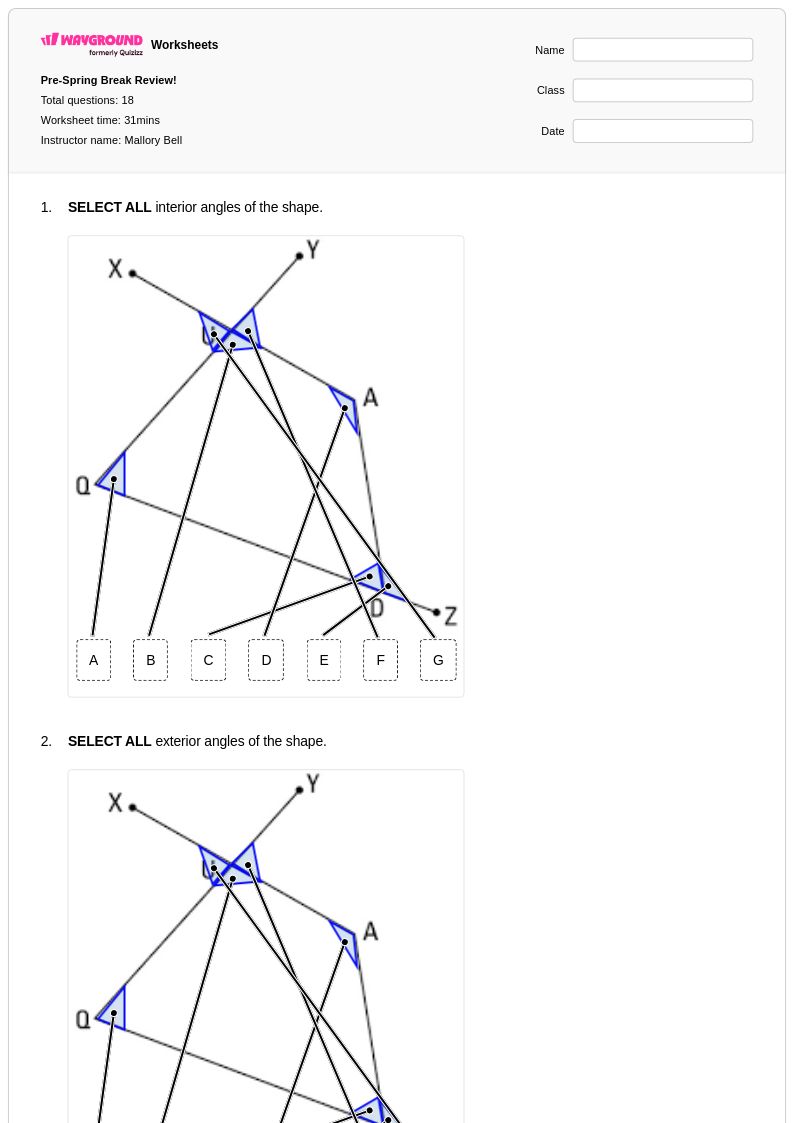
18Q
9th - 12th
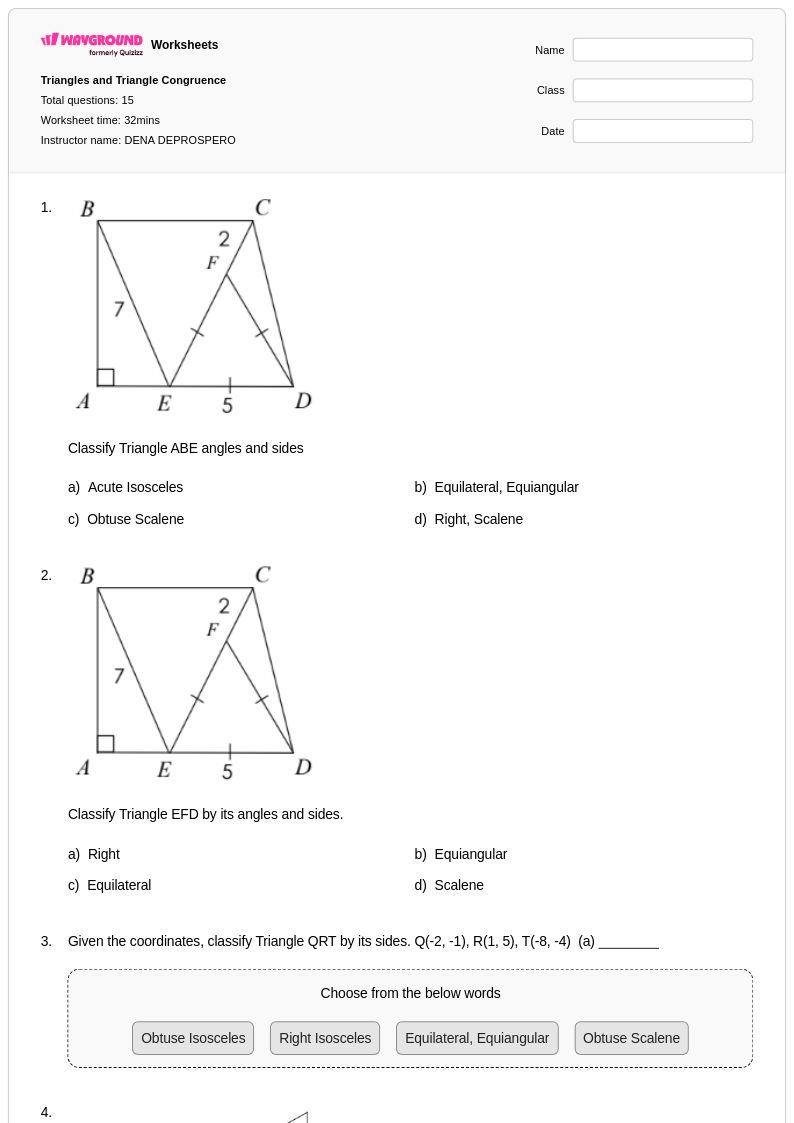
15Q
9th - 12th

10Q
8th
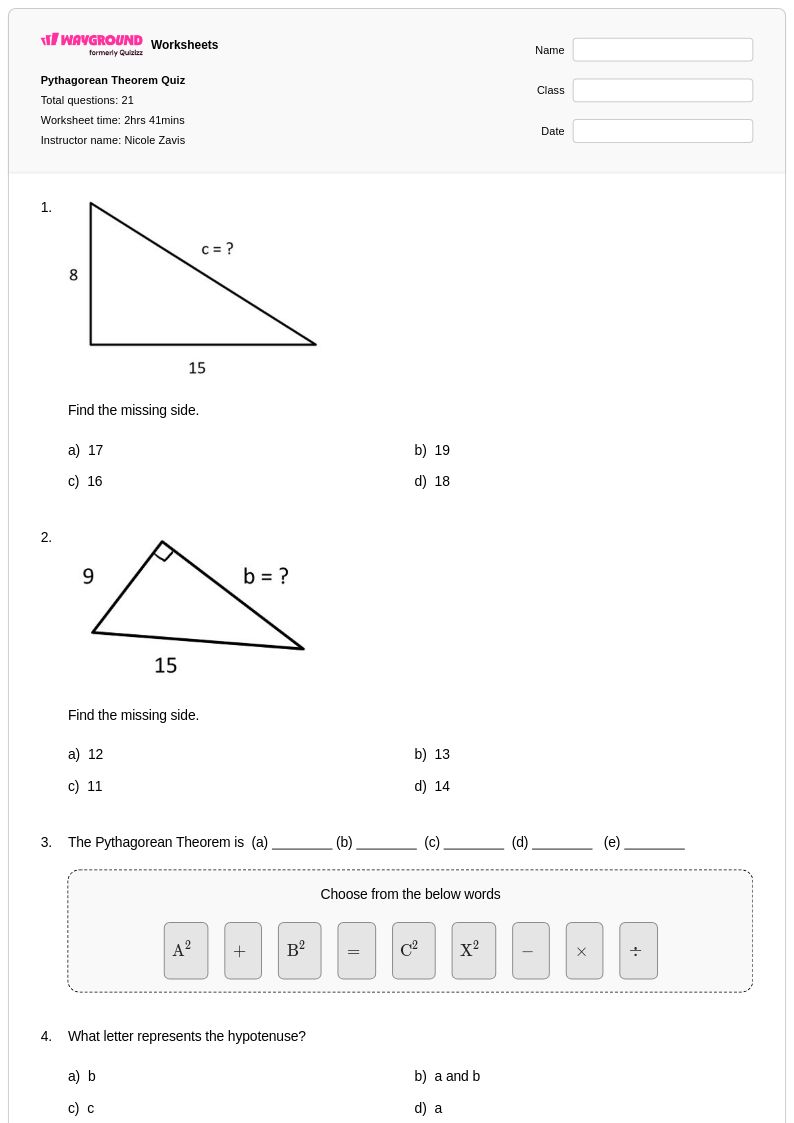
21Q
10th

201Q
8th
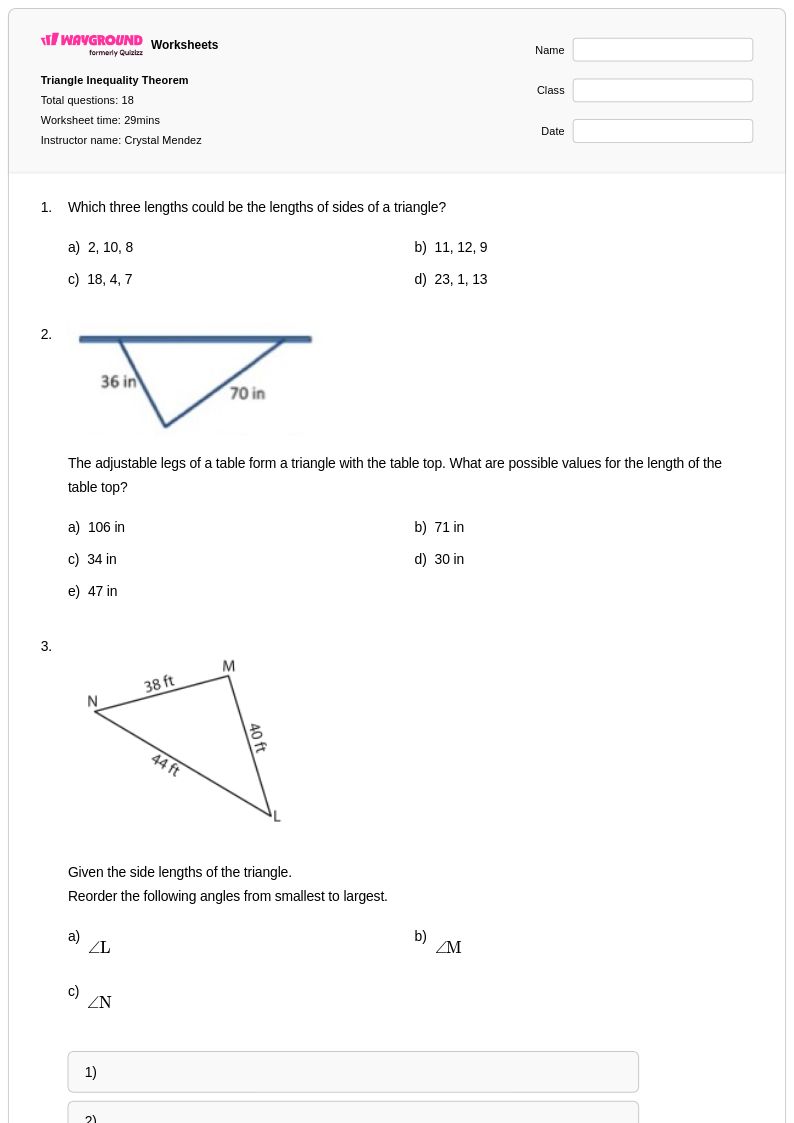
18Q
10th

20Q
8th - Uni

16Q
10th
30Q
10th

17Q
10th
Explorar hojas de trabajo por materias
สำรวจแผ่นงาน ทฤษฎีบทสามเหลี่ยมหน้าจั่ว ที่พิมพ์ได้
แบบฝึกหัดทฤษฎีบทสามเหลี่ยมหน้าจั่วจาก Wayground (เดิมคือ Quizizz) มอบโอกาสในการฝึกฝนอย่างครอบคลุมเพื่อให้นักเรียนเชี่ยวชาญหลักการพื้นฐานทางเรขาคณิตข้อหนึ่ง แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยให้นักเรียนเข้าใจว่ามุมฐานของสามเหลี่ยมหน้าจั่วมีขนาดเท่ากัน พร้อมทั้งพัฒนาทักษะที่จำเป็นในการวัดมุม การจำแนกประเภทสามเหลี่ยม และการสร้างบทพิสูจน์ทางเรขาคณิต ชุดแบบฝึกหัดประกอบด้วยโจทย์ฝึกฝนที่หลากหลาย ตั้งแต่การระบุมุมพื้นฐานไปจนถึงบทพิสูจน์หลายขั้นตอนที่ซับซ้อน โดยแต่ละแบบฝึกหัดมีเฉลยคำตอบโดยละเอียดเพื่อสนับสนุนการเรียนรู้ด้วยตนเองและการประเมินตนเอง นักเรียนจะได้ทำแบบฝึกหัดที่ดาวน์โหลดได้ฟรี ซึ่งจะช่วยเสริมสร้างการประยุกต์ใช้ทฤษฎีบทในบริบทของโลกแห่งความเป็นจริง สร้างความมั่นใจในการใช้เหตุผลทางเรขาคณิต พร้อมทั้งเสริมสร้างความสามารถในการจดจำและประยุกต์ใช้ความสัมพันธ์ที่สำคัญนี้ในสถานการณ์ทางคณิตศาสตร์ต่างๆ
Wayground (เดิมคือ Quizizz) ช่วยเสริมศักยภาพให้แก่ครูผู้สอนด้วยแหล่งข้อมูลทฤษฎีบทสามเหลี่ยมหน้าจั่วที่สร้างโดยครูหลายล้านรายการ ซึ่งช่วยลดความยุ่งยากในการวางแผนบทเรียนและยกระดับคุณภาพการสอน แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานทางคณิตศาสตร์เฉพาะได้อย่างรวดเร็ว ในขณะที่เครื่องมือการปรับระดับความยากง่ายช่วยให้สามารถปรับแต่งได้อย่างราบรื่นเพื่อตอบสนองความต้องการในการเรียนรู้และระดับความสามารถที่หลากหลาย ชุดแบบฝึกหัดที่ครอบคลุมเหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่สามารถพิมพ์ได้และเวอร์ชันดิจิทัลแบบโต้ตอบได้ ทำให้มีความยืดหยุ่นสำหรับการสอนในห้องเรียน การบ้าน และการเตรียมการประเมิน ครูสามารถใช้ทรัพยากรที่หลากหลายเหล่านี้สำหรับการฝึกฝนทักษะเฉพาะด้าน การสนับสนุนการแก้ไขปัญหาสำหรับผู้เรียนที่ประสบปัญหา และโอกาสในการเสริมสร้างความรู้สำหรับนักเรียนที่มีความสามารถสูง เพื่อให้มั่นใจว่าผู้เรียนทุกคนสามารถพัฒนาความเชี่ยวชาญในแนวคิดทางเรขาคณิตที่สำคัญนี้ได้ผ่านประสบการณ์ทางคณิตศาสตร์ที่ท้าทายและน่าสนใจอย่างเหมาะสม
