
16Q
5th

20Q
5th
16Q
9th - 12th

9Q
2nd

17Q
5th - 6th
10Q
6th - Uni

14Q
6th - Uni

15Q
3rd

15Q
3rd - Uni

13Q
9th - Uni

16Q
6th - Uni

15Q
5th - Uni

13Q
6th - Uni
12Q
5th

15Q
4th

11Q
5th

24Q
6th

10Q
6th
34Q
6th
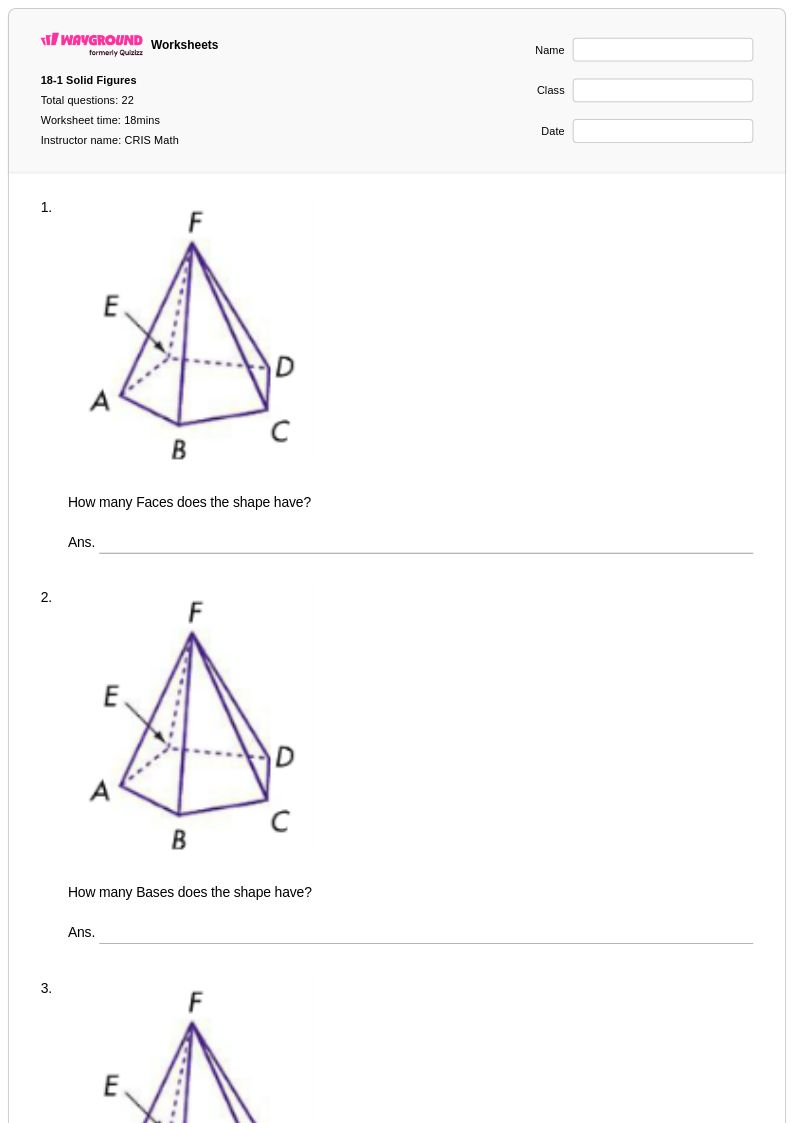
22Q
6th

15Q
6th - Uni
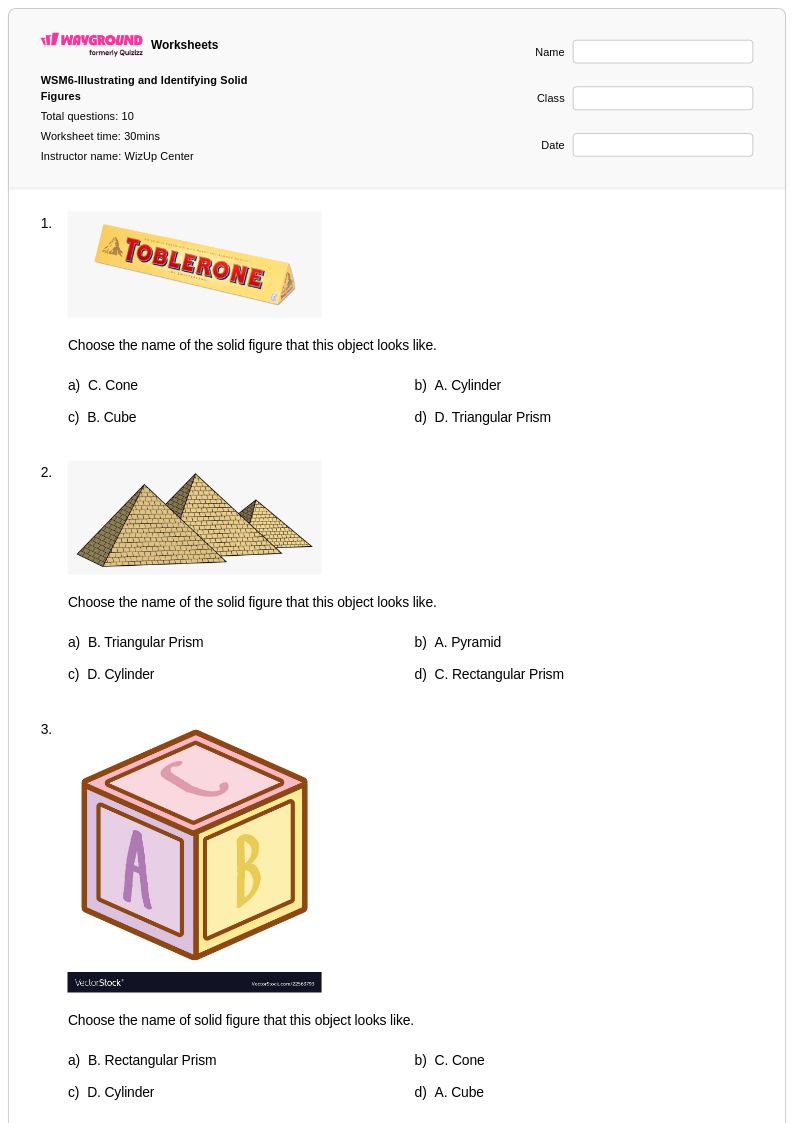
10Q
6th
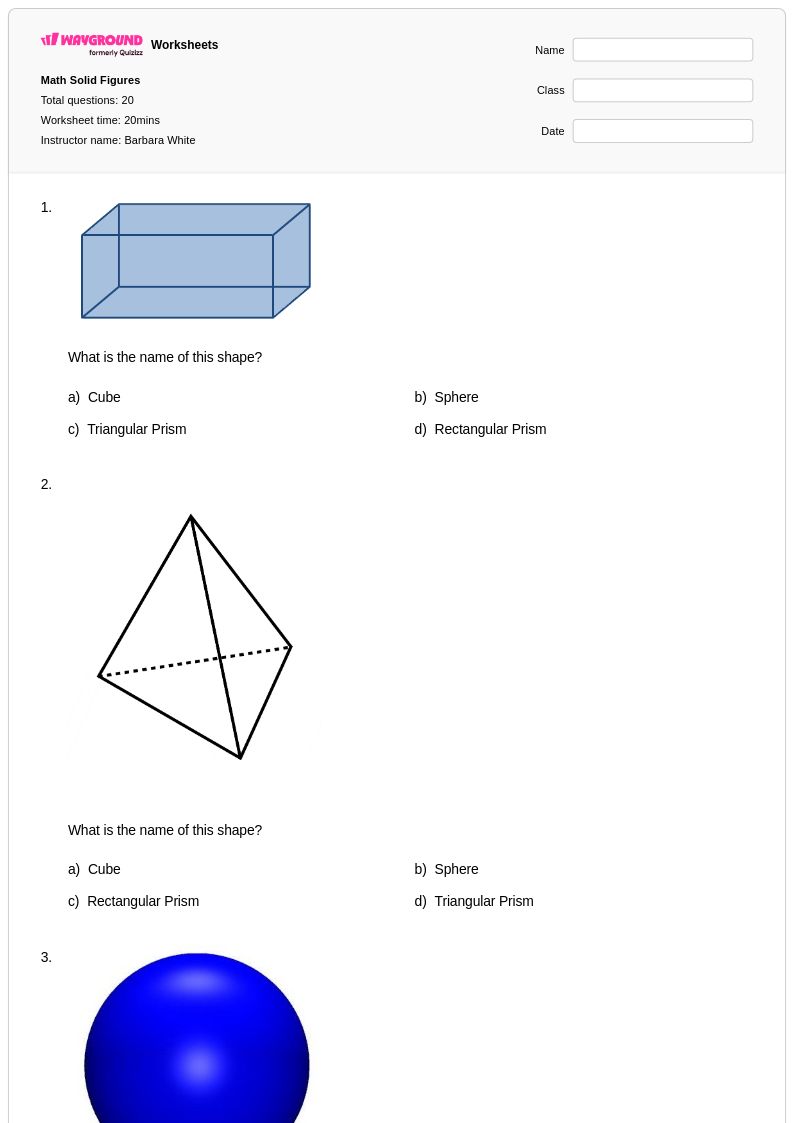
20Q
2nd

5Q
6th
Explorar hojas de trabajo por materias
สำรวจแผ่นงาน รูปทรงตัน ที่พิมพ์ได้
แบบฝึกหัดรูปทรงเรขาคณิตสามมิติจาก Wayground (เดิมคือ Quizizz) เป็นแหล่งข้อมูลทางคณิตศาสตร์ที่ครอบคลุม ช่วยเสริมสร้างทักษะเรขาคณิตสามมิติของนักเรียนผ่านการฝึกฝนและการสำรวจอย่างเป็นระบบ แบบฝึกหัดที่ออกแบบมาอย่างเชี่ยวชาญเหล่านี้มุ่งเน้นไปที่แนวคิดที่สำคัญ เช่น การระบุคุณสมบัติของลูกบาศก์ ปริซึมสี่เหลี่ยม ทรงกระบอก กรวย ทรงกลม และพีระมิด พร้อมทั้งพัฒนาความสามารถในการให้เหตุผลเชิงพื้นที่ซึ่งมีความสำคัญต่อความเข้าใจทางเรขาคณิต นักเรียนจะได้ฝึกฝนโจทย์ปัญหาที่ครอบคลุมการคำนวณพื้นที่ผิว สูตรปริมาตร การสร้างแบบจำลอง และการวิเคราะห์ภาคตัดขวาง ซึ่งเป็นการสร้างทักษะพื้นฐานที่จำเป็นสำหรับแนวคิดทางเรขาคณิตขั้นสูง แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียด และมีให้ดาวน์โหลดเป็นไฟล์ PDF ฟรี ช่วยให้ครูผู้สอนสามารถบูรณาการการสอนรูปทรงเรขาคณิตสามมิติเข้ากับหลักสูตรคณิตศาสตร์ได้อย่างราบรื่น พร้อมทั้งมอบโอกาสให้นักเรียนได้ฝึกฝนความสัมพันธ์สามมิติที่ซับซ้อนอย่างเป็นระบบ
Wayground (เดิมคือ Quizizz) สนับสนุนครูผู้สอนคณิตศาสตร์ด้วยแบบฝึกหัดรูปทรงเรขาคณิตสามมิติที่สร้างโดยครูหลายล้านชุด มีระบบค้นหาและกรองข้อมูลที่มีประสิทธิภาพ ช่วยให้เข้าถึงสื่อการเรียนการสอนที่เหมาะสมกับระดับชั้นและสอดคล้องกับมาตรฐานได้อย่างรวดเร็ว แพลตฟอร์มนี้มีเครื่องมือการสอนที่ครอบคลุมและยอดเยี่ยม ช่วยให้ครูสามารถปรับแต่งแบบฝึกหัดตามความต้องการและวัตถุประสงค์การเรียนรู้ของนักเรียนแต่ละคน ไม่ว่าจะเป็นการแก้ไขปัญหาพื้นฐานเกี่ยวกับการระบุรูปทรงเรขาคณิตสามมิติ หรือการเสริมสร้างความรู้ผ่านการประยุกต์ใช้ปริมาตรและพื้นที่ผิวขั้นสูง แหล่งข้อมูลที่ยืดหยุ่นเหล่านี้มีให้เลือกทั้งแบบพิมพ์ได้และแบบดิจิทัล รวมถึงไฟล์ PDF ที่ดาวน์โหลดได้ ทำให้การวางแผนบทเรียนมีประสิทธิภาพ พร้อมทั้งมีตัวเลือกมากมายสำหรับการฝึกฝนทักษะและการประเมินผล ครูสามารถใช้ประโยชน์จากสื่อที่คัดสรรมาอย่างดีเหล่านี้เพื่อสร้างประสบการณ์การเรียนรู้ที่ตรงเป้าหมาย ซึ่งตอบสนองรูปแบบการเรียนรู้ที่หลากหลายและสนับสนุนความก้าวหน้าอย่างเป็นระบบในแนวคิดเกี่ยวกับรูปทรงเรขาคณิตสามมิติ ตั้งแต่การจดจำรูปทรงพื้นฐานไปจนถึงกลยุทธ์การแก้ปัญหาทางเรขาคณิตที่ซับซ้อน
