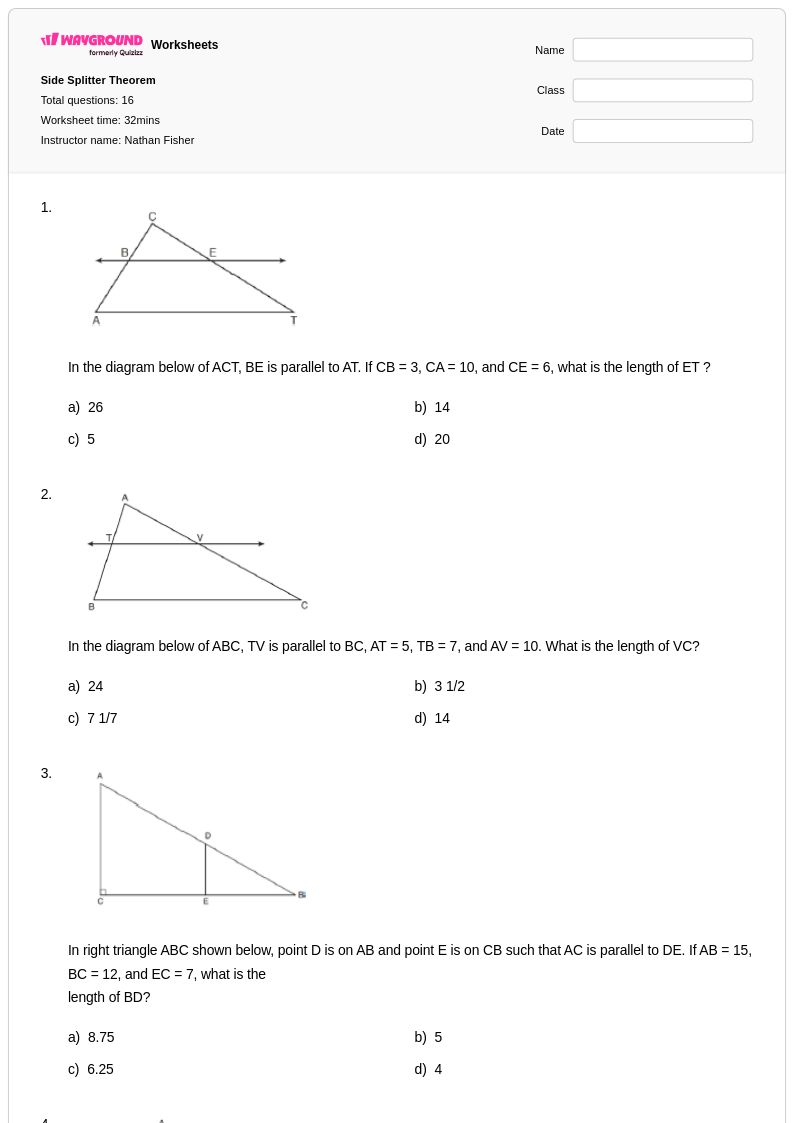
16 คิว
9th - 12th
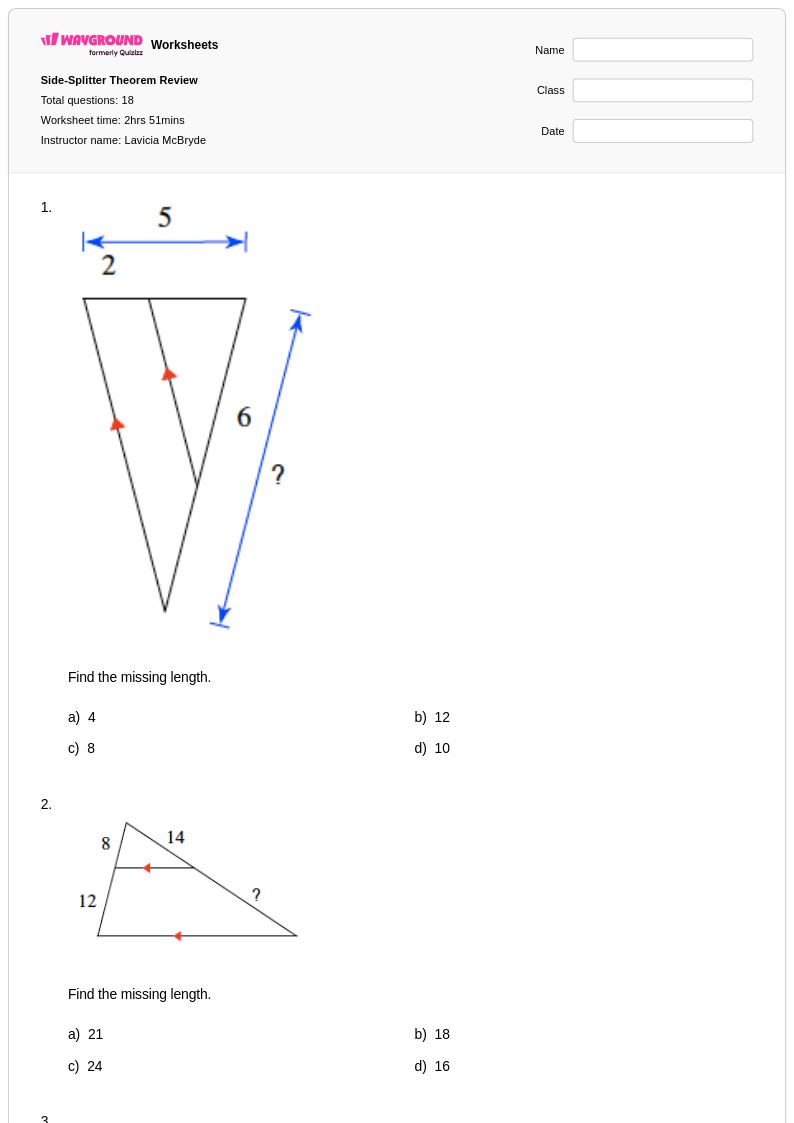
18 คิว
10th - Uni
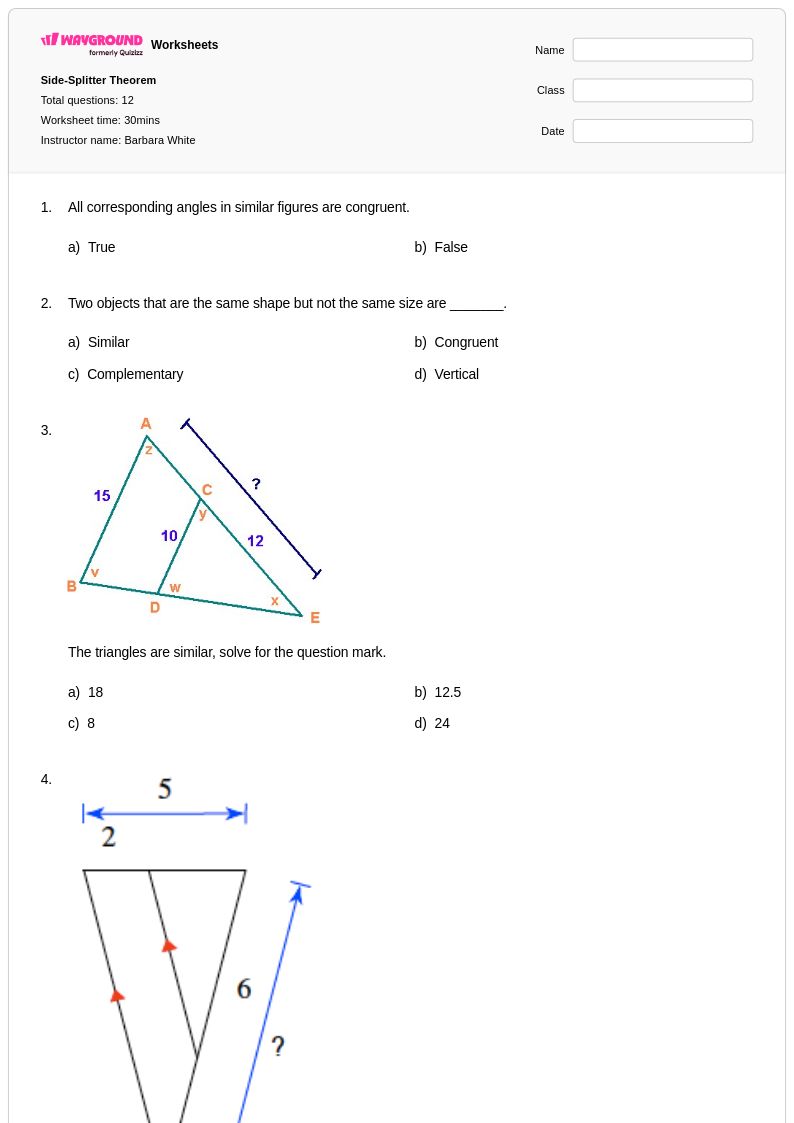
12 คิว
9th - 10th
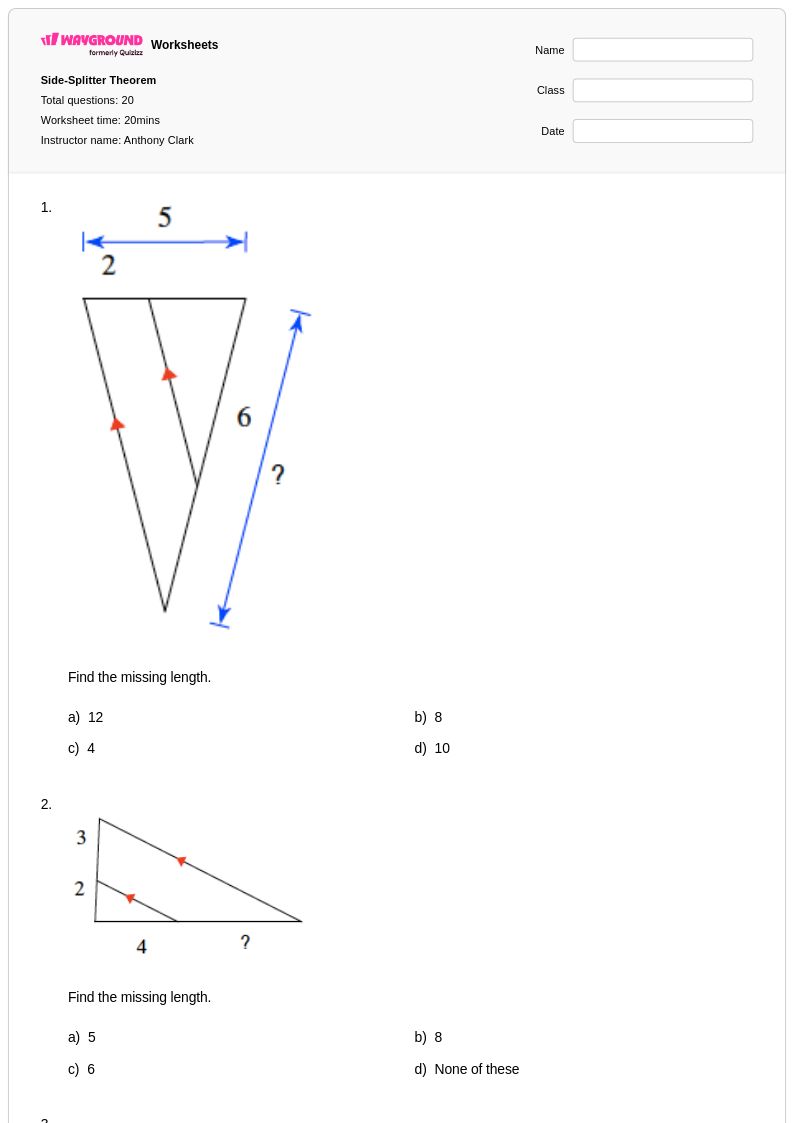
20 คิว
10th - Uni

10 คิว
10th
12 คิว
9th - 10th
21 คิว
10th
8 คิว
9th - 12th
20 คิว
10th
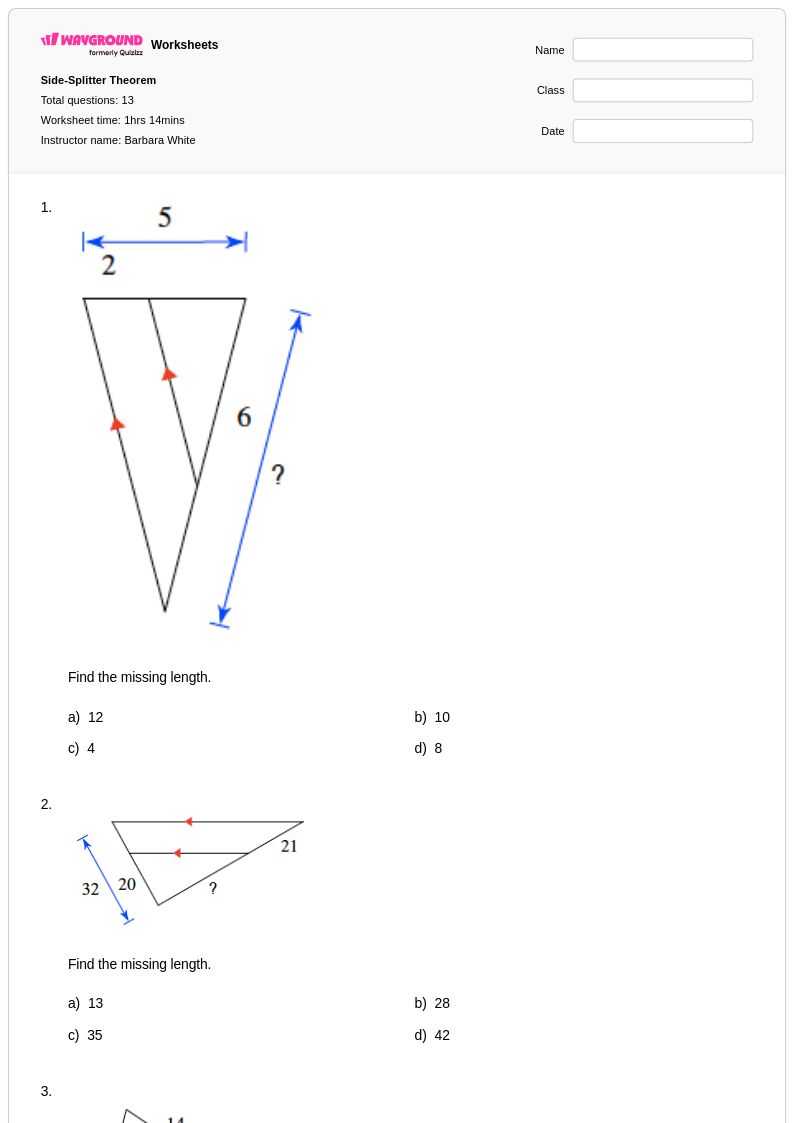
13 คิว
9th - 12th
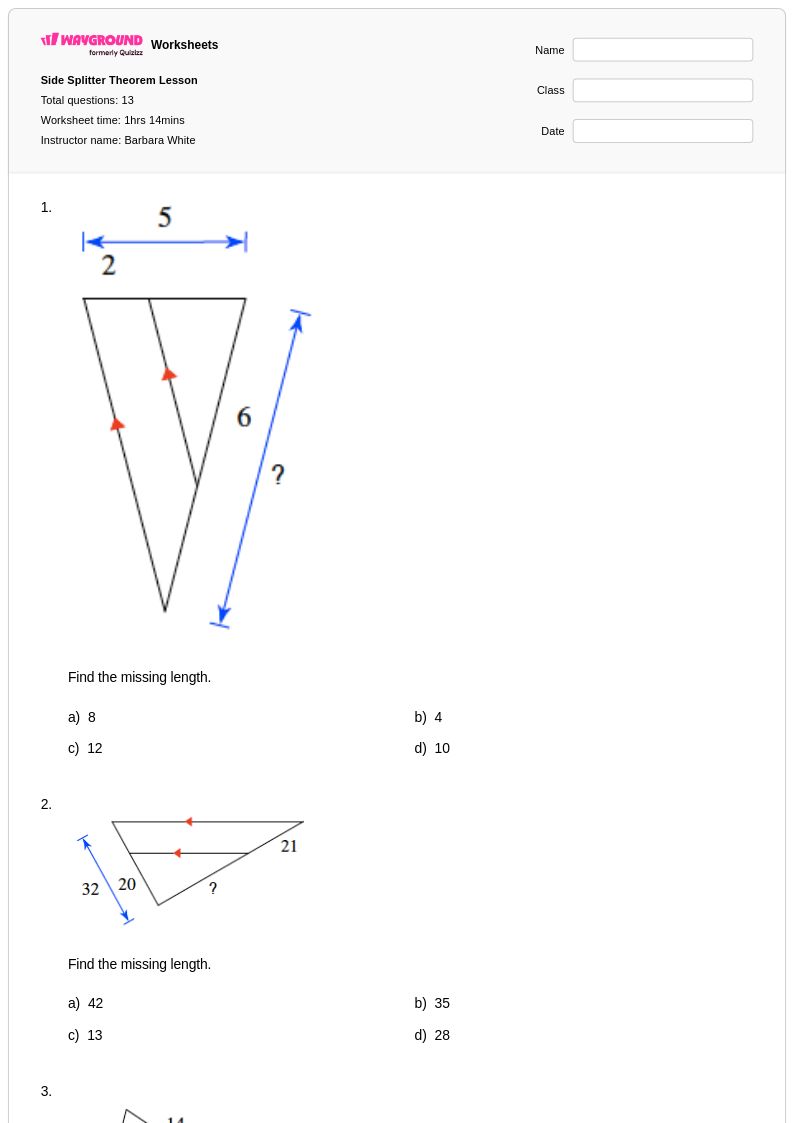
13 คิว
9th - 12th
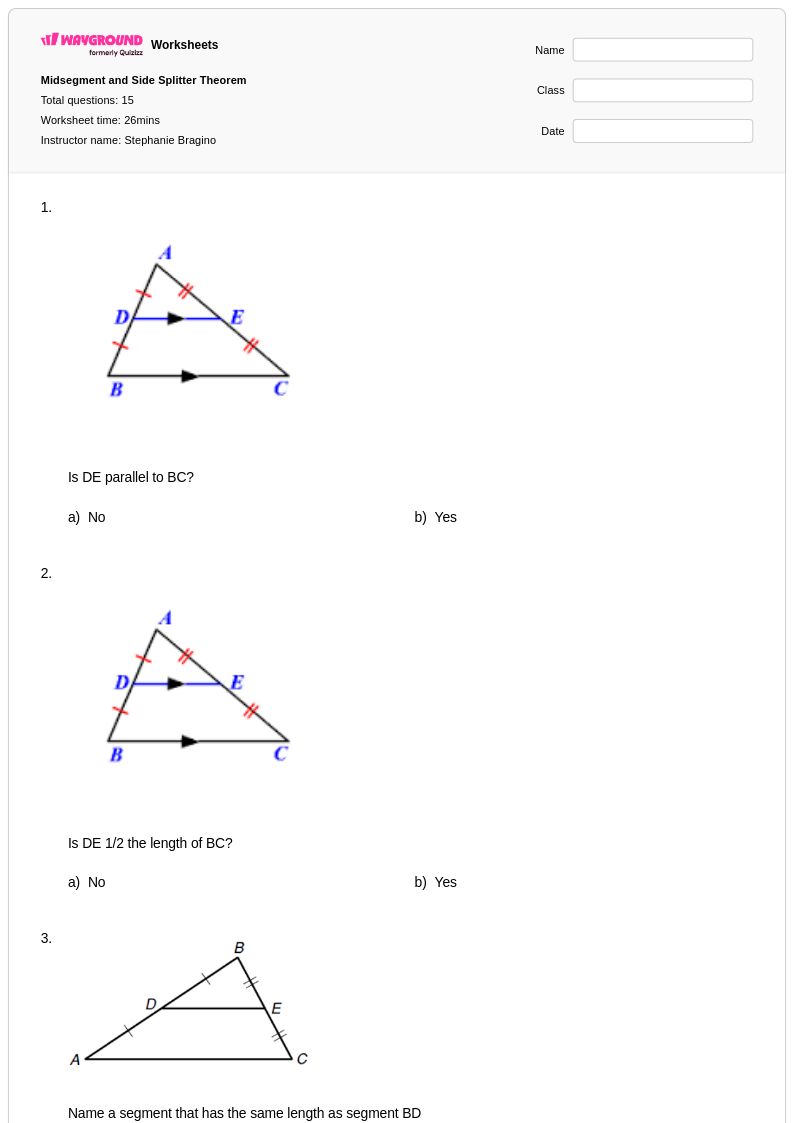
15 คิว
9th
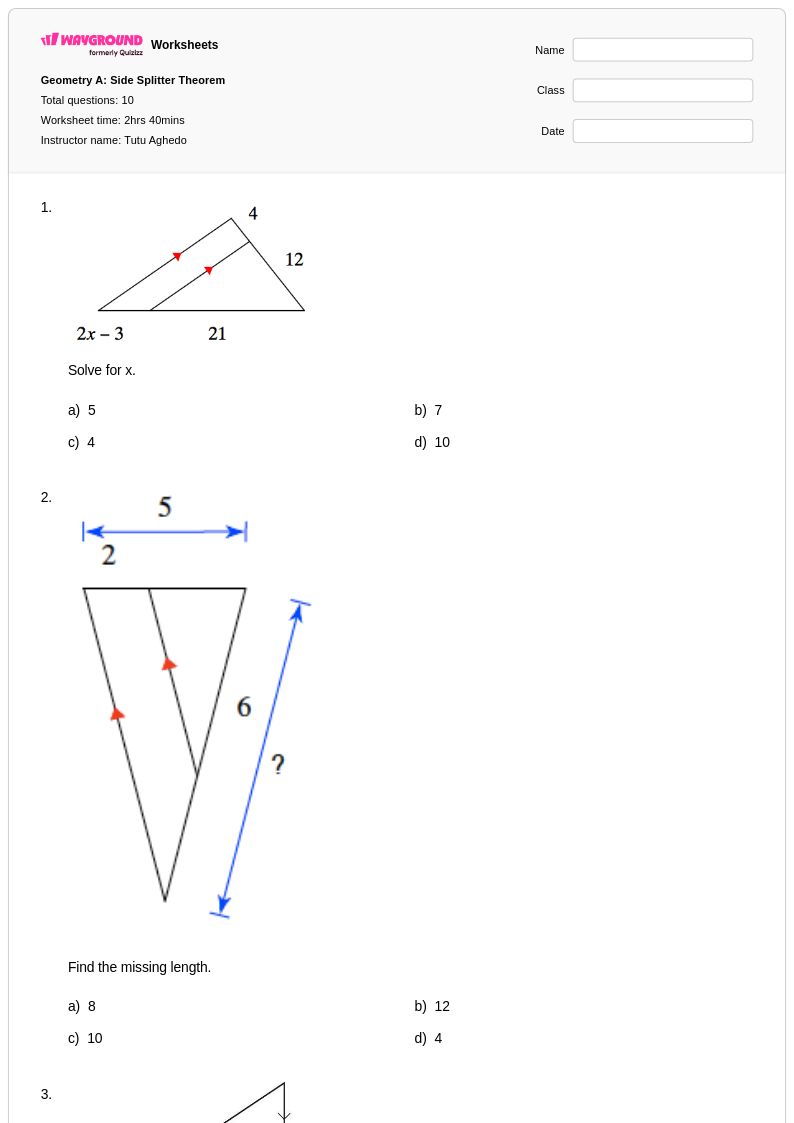
10 คิว
10th

23 คิว
10th
20 คิว
10th - Uni

46 คิว
10th

20 คิว
9th - Uni
21 คิว
10th
20 คิว
10th - Uni
13 คิว
10th

20 คิว
7th - Uni

26 คิว
10th

25 คิว
10th

14 คิว
8th - 10th
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน ทฤษฎีตัวแยกด้านข้าง ที่พิมพ์ได้
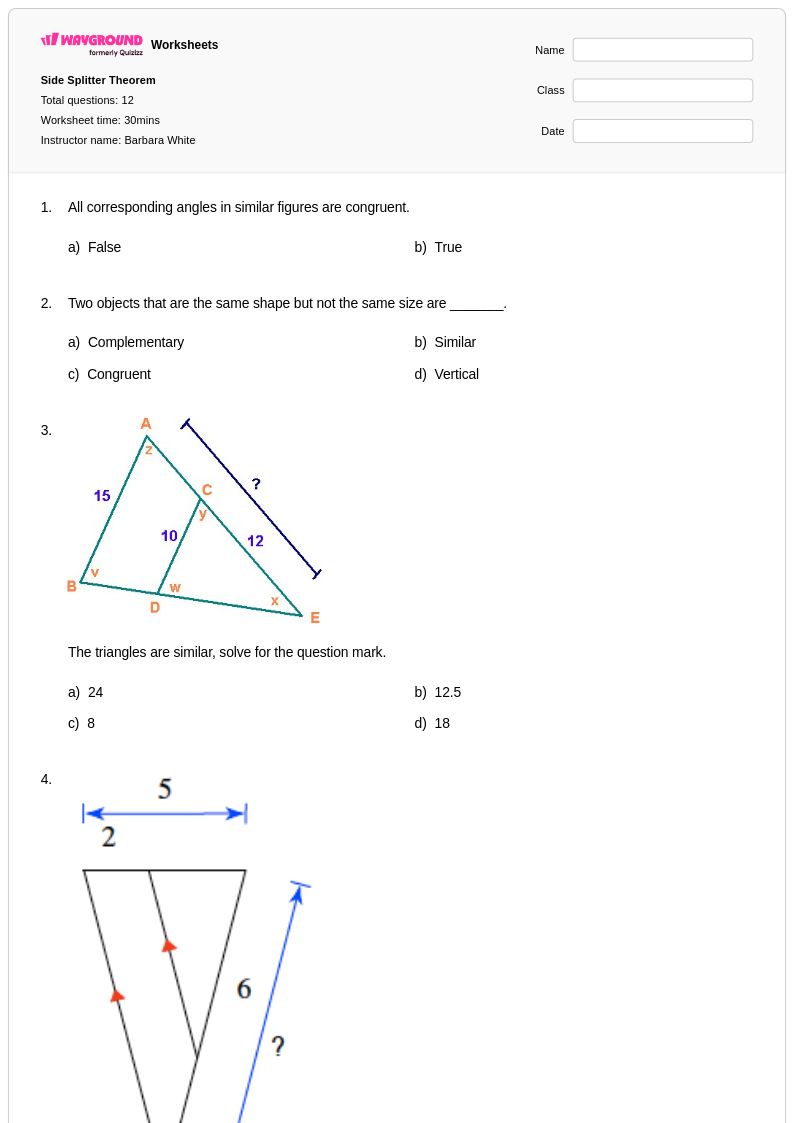
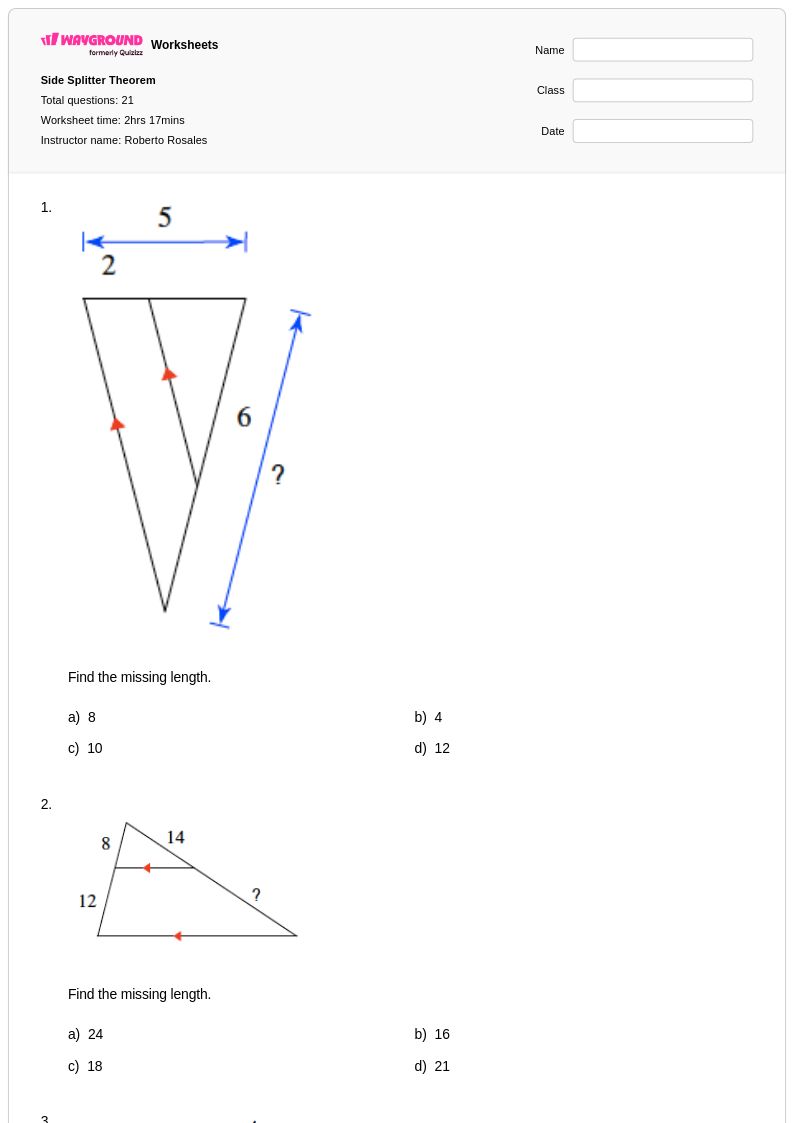
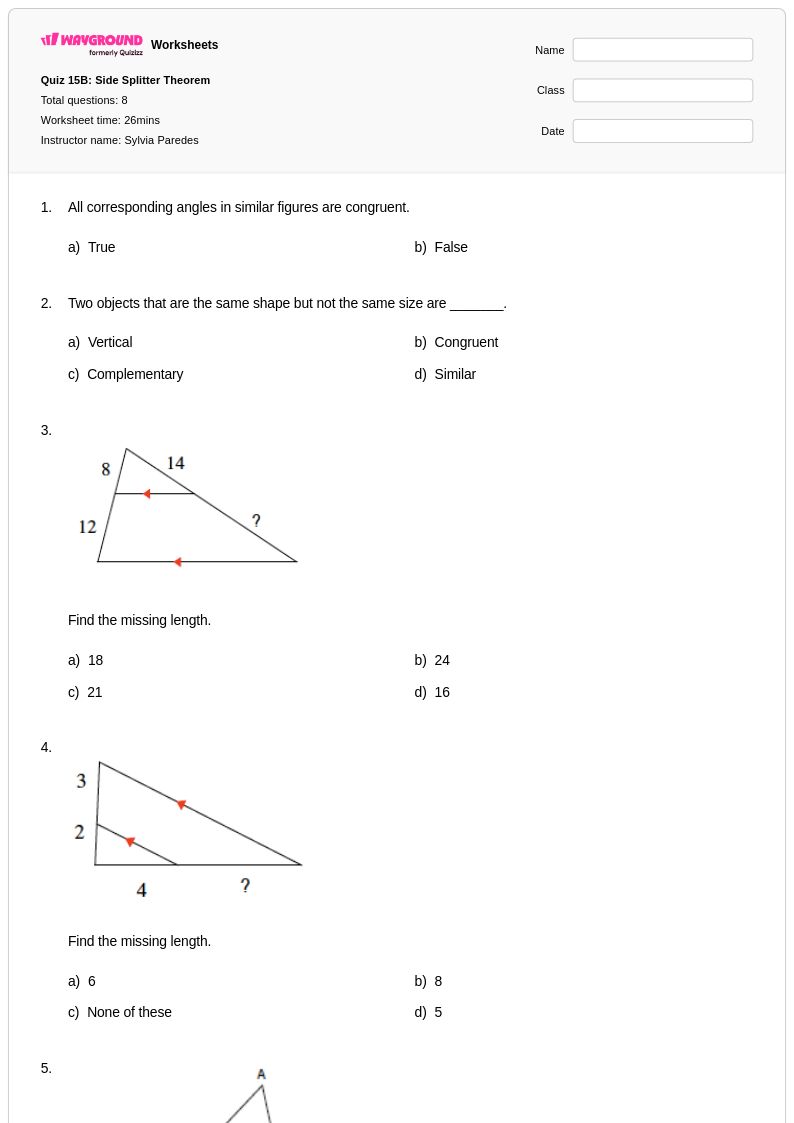
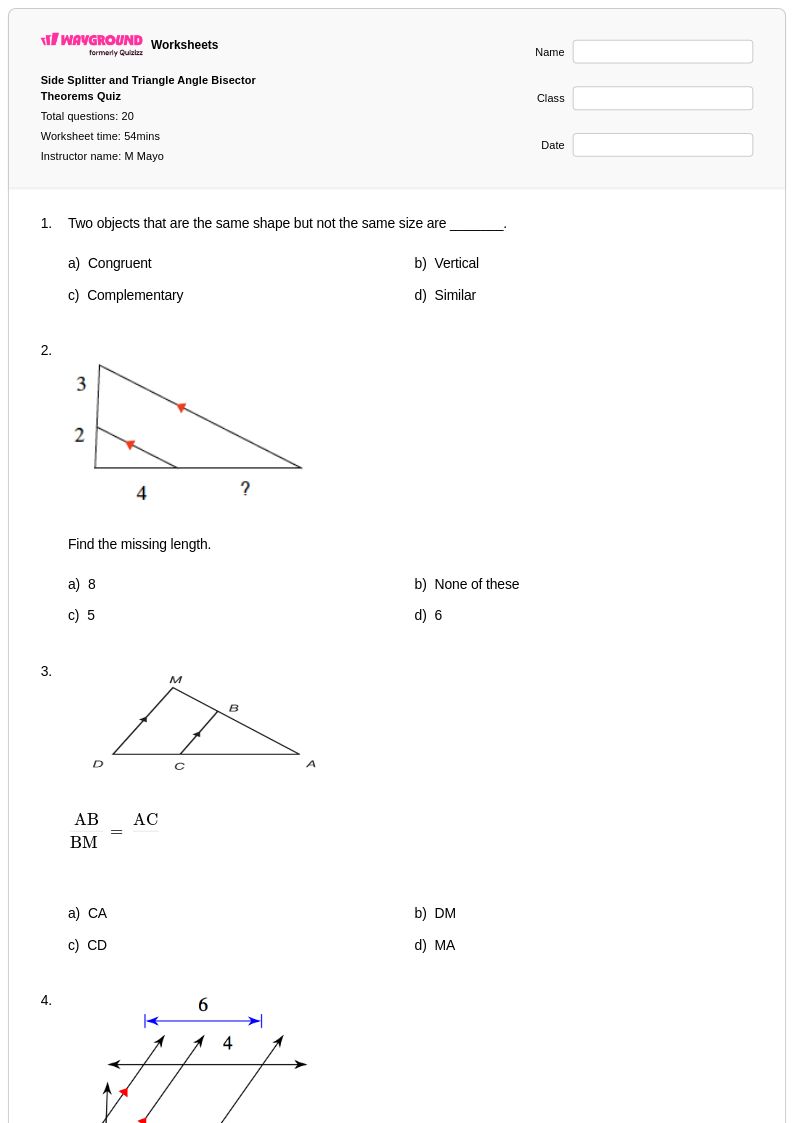
แบบฝึกหัดทฤษฎีบทการแบ่งด้าน (Side Splitter Theorem) จาก Wayground (เดิมคือ Quizizz) มอบโอกาสในการฝึกฝนอย่างครอบคลุมสำหรับนักเรียน เพื่อให้เชี่ยวชาญแนวคิดทางเรขาคณิตพื้นฐานนี้ ซึ่งแสดงให้เห็นถึงความสัมพันธ์ตามสัดส่วนในรูปสามเหลี่ยม แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ มุ่งเน้นการพัฒนาความสามารถของนักเรียนในการระบุส่วนของเส้นตรงที่ขนานกันซึ่งตัดกับด้านของรูปสามเหลี่ยม และคำนวณค่าที่ไม่ทราบค่าโดยใช้เหตุผลตามสัดส่วน แบบฝึกหัดเหล่านี้เสริมสร้างทักษะที่สำคัญ ได้แก่ การตั้งสัดส่วน การคูณไขว้เพื่อหาค่าตัวแปร และการประยุกต์ใช้ทฤษฎีบทเพื่อแก้ปัญหาทางเรขาคณิตในโลกแห่งความเป็นจริง แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียด ซึ่งสนับสนุนทั้งการเรียนรู้ด้วยตนเองและการเรียนการสอนในห้องเรียน พร้อมด้วยสื่อสิ่งพิมพ์ฟรีในรูปแบบ PDF ที่สะดวกต่อการแจกจ่ายและการฝึกฝน
Wayground (เดิมคือ Quizizz) ช่วยให้ครูผู้สอนมีแหล่งข้อมูลทฤษฎีบทการแบ่งด้านที่สร้างโดยครูหลายล้านรายการ ซึ่งมีระบบค้นหาและกรองข้อมูลที่มีประสิทธิภาพ เพื่อค้นหาสื่อที่สอดคล้องกับมาตรฐานหลักสูตรและวัตถุประสงค์การเรียนรู้เฉพาะ เครื่องมือการปรับระดับความยากง่ายของแพลตฟอร์ม ช่วยให้ครูสามารถปรับแต่งแบบฝึกหัดสำหรับระดับทักษะต่างๆ โดยให้การสนับสนุนการแก้ไขปัญหาสำหรับนักเรียนที่ประสบปัญหา และโอกาสในการเสริมสร้างความรู้สำหรับผู้เรียนที่มีความสามารถสูง สื่อการเรียนรู้ที่ยืดหยุ่นเหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่สามารถพิมพ์ได้สำหรับการใช้งานในห้องเรียนแบบดั้งเดิม และรูปแบบดิจิทัลสำหรับการเรียนการสอนออนไลน์แบบโต้ตอบ ทำให้การวางแผนบทเรียนมีประสิทธิภาพและประสิทธิผลมากยิ่งขึ้น ครูสามารถบูรณาการสื่อเหล่านี้เข้ากับหลักสูตรเรขาคณิตได้อย่างราบรื่น เพื่อให้การฝึกฝนทักษะที่ตรงเป้าหมาย ประเมินความเข้าใจของนักเรียนเกี่ยวกับความสัมพันธ์ตามสัดส่วนในรูปสามเหลี่ยม และสนับสนุนนักเรียนในการพัฒนาการให้เหตุผลทางคณิตศาสตร์ที่จำเป็นต่อความสำเร็จในแนวคิดเรขาคณิตขั้นสูง
