
50 คิว
8th - 9th
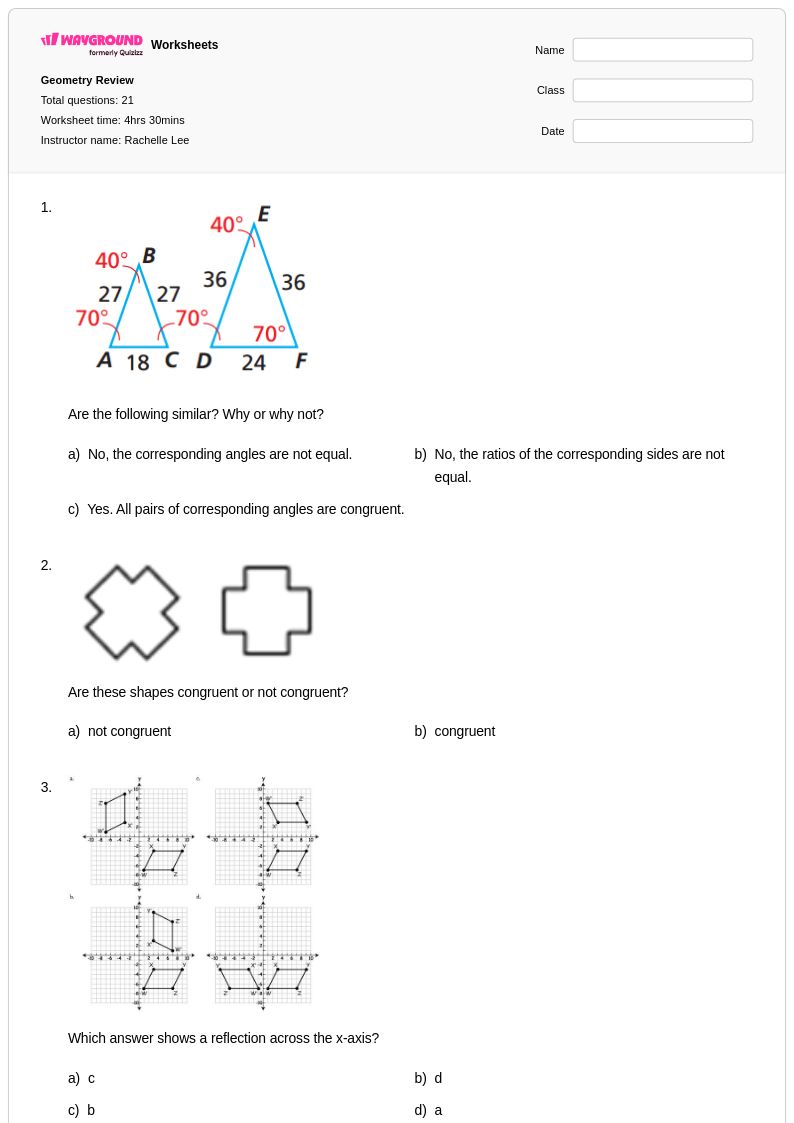
21 คิว
8th
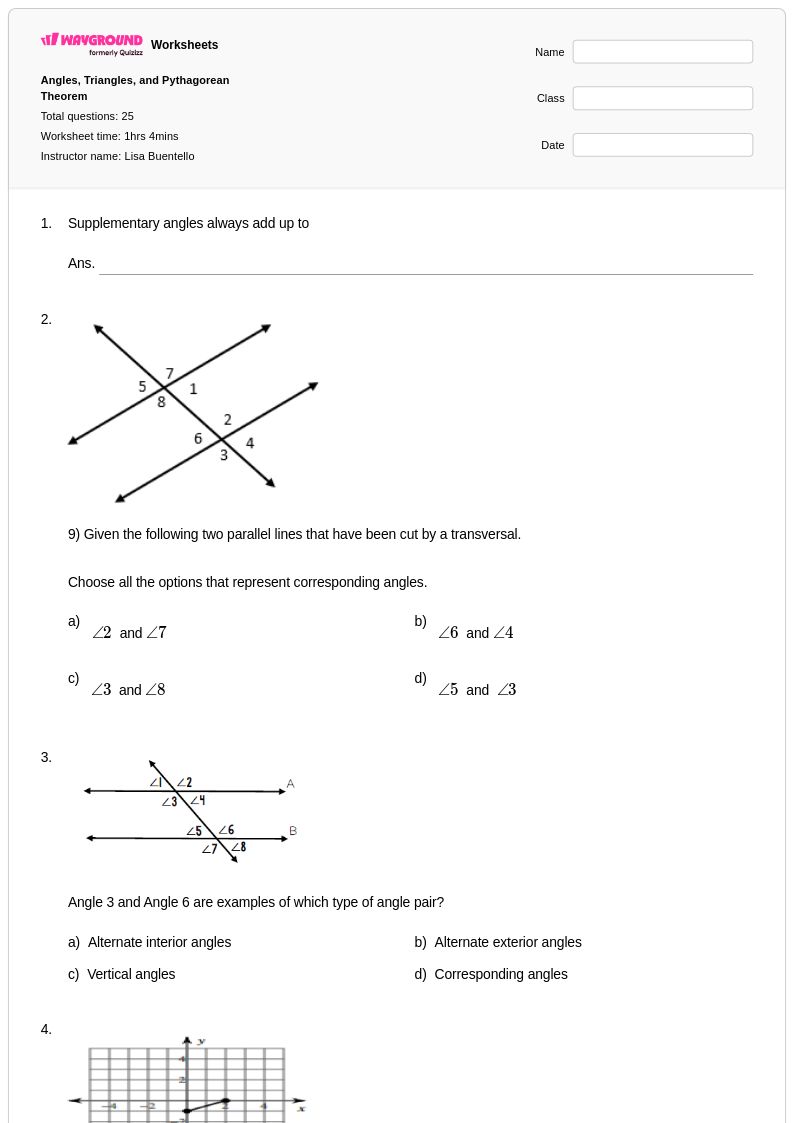
25 คิว
8th
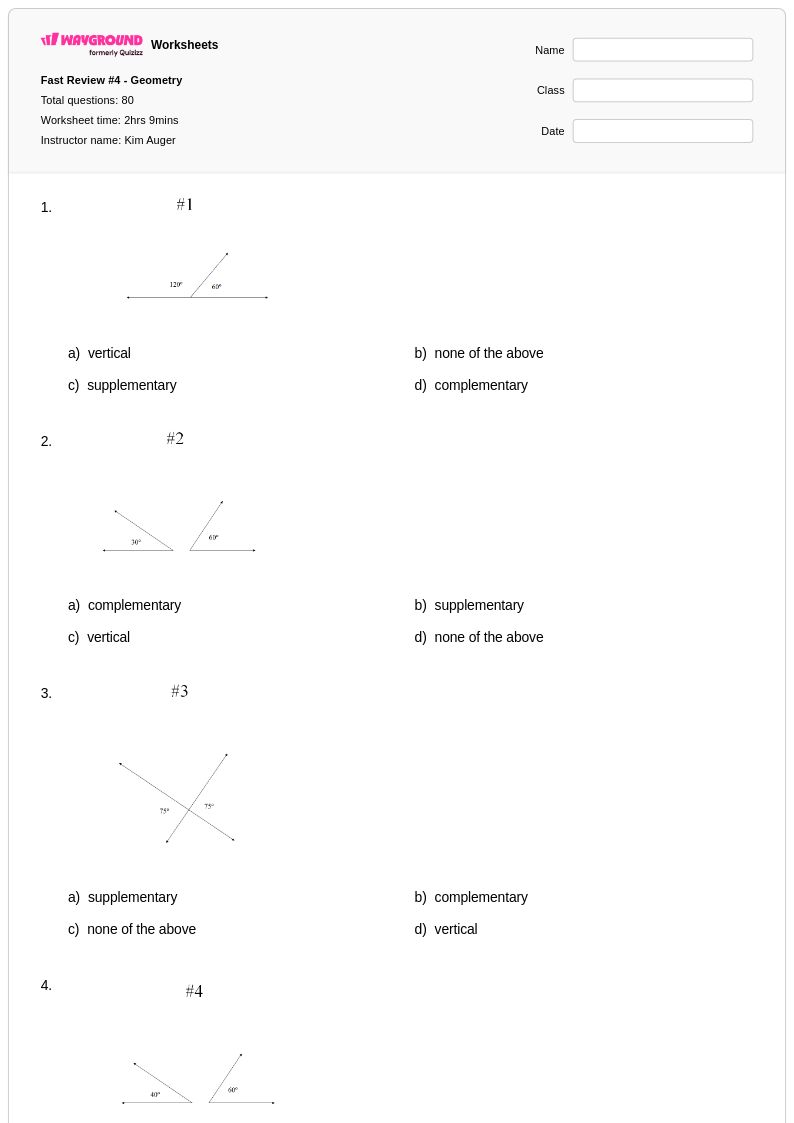
80 คิว
8th
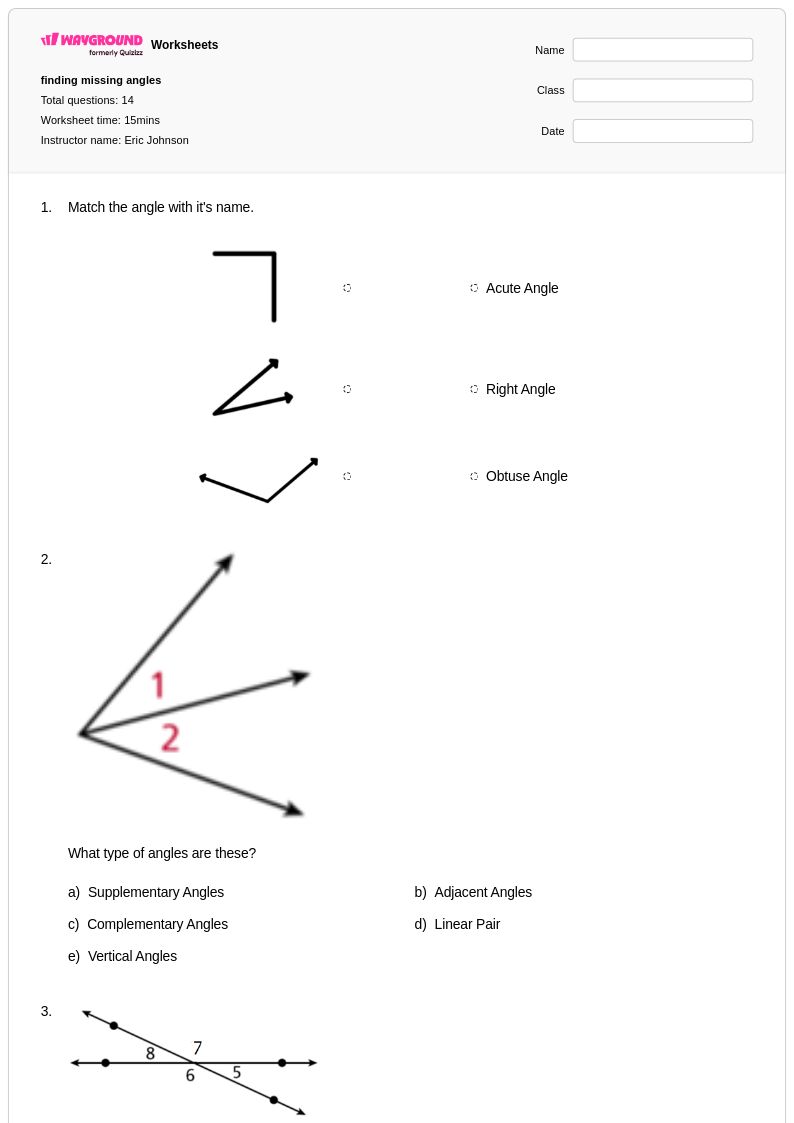
14 คิว
8th - Uni
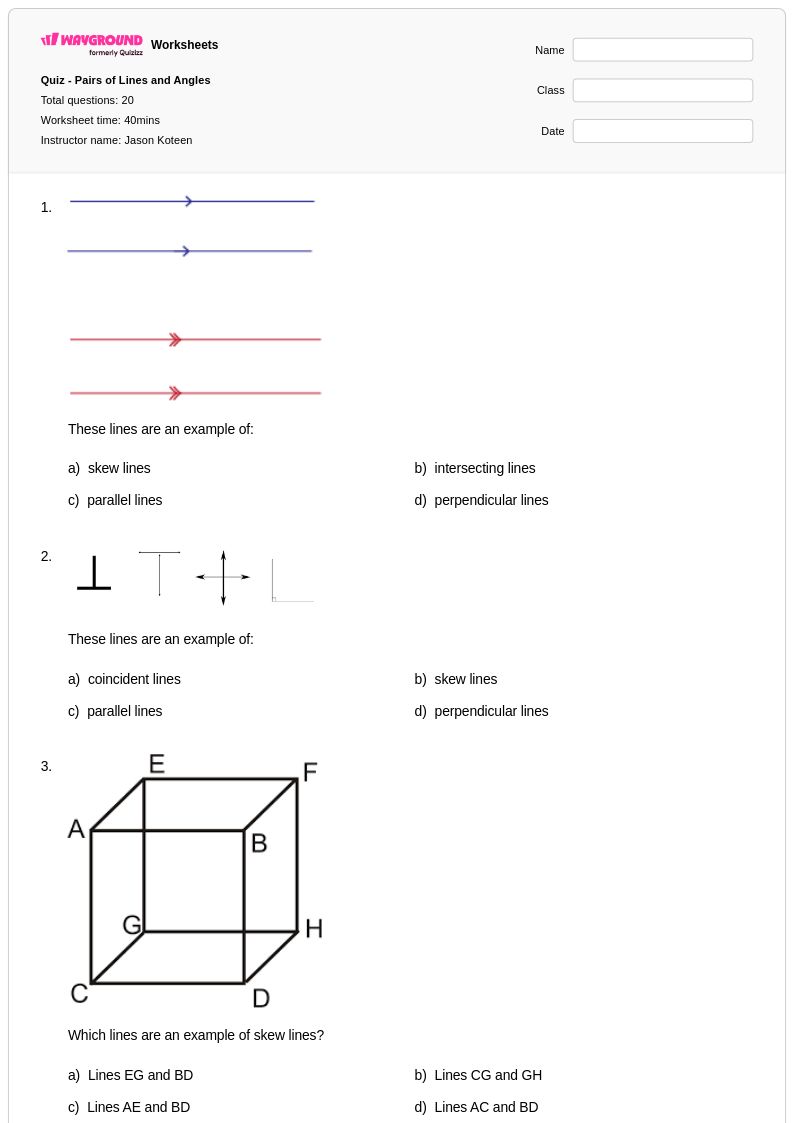
20 คิว
7th - 10th
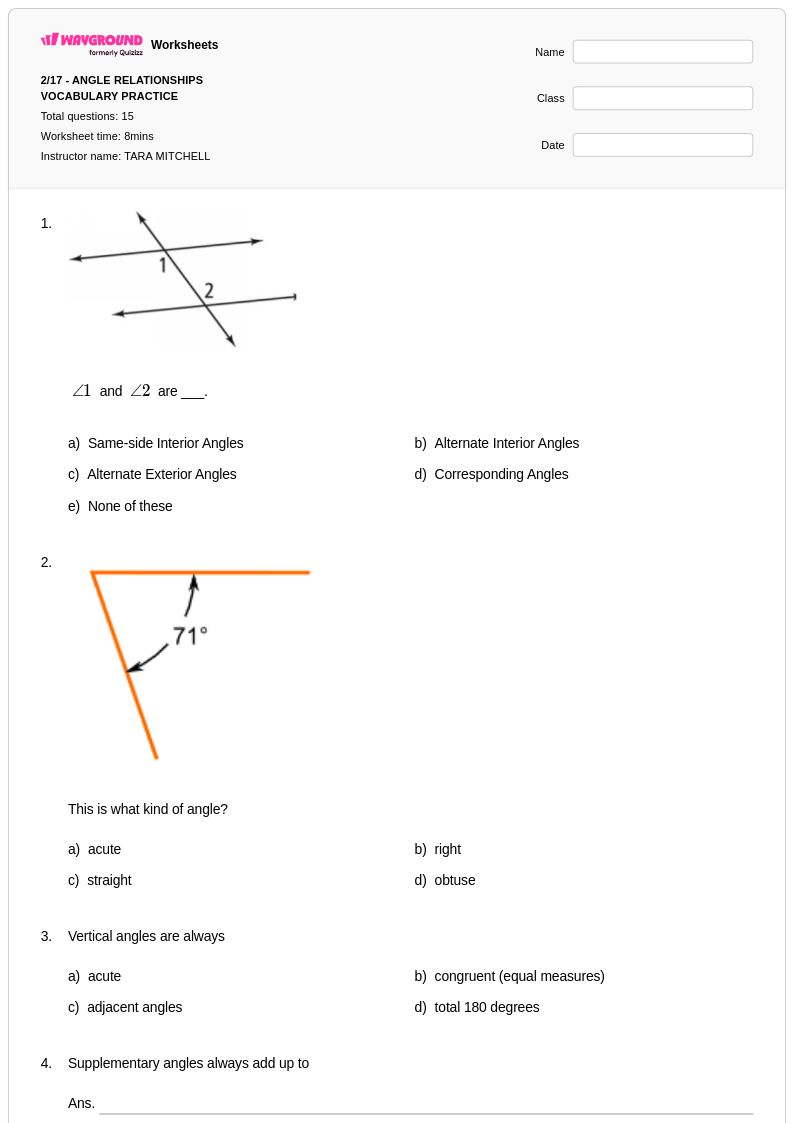
15 คิว
8th

17 คิว
8th
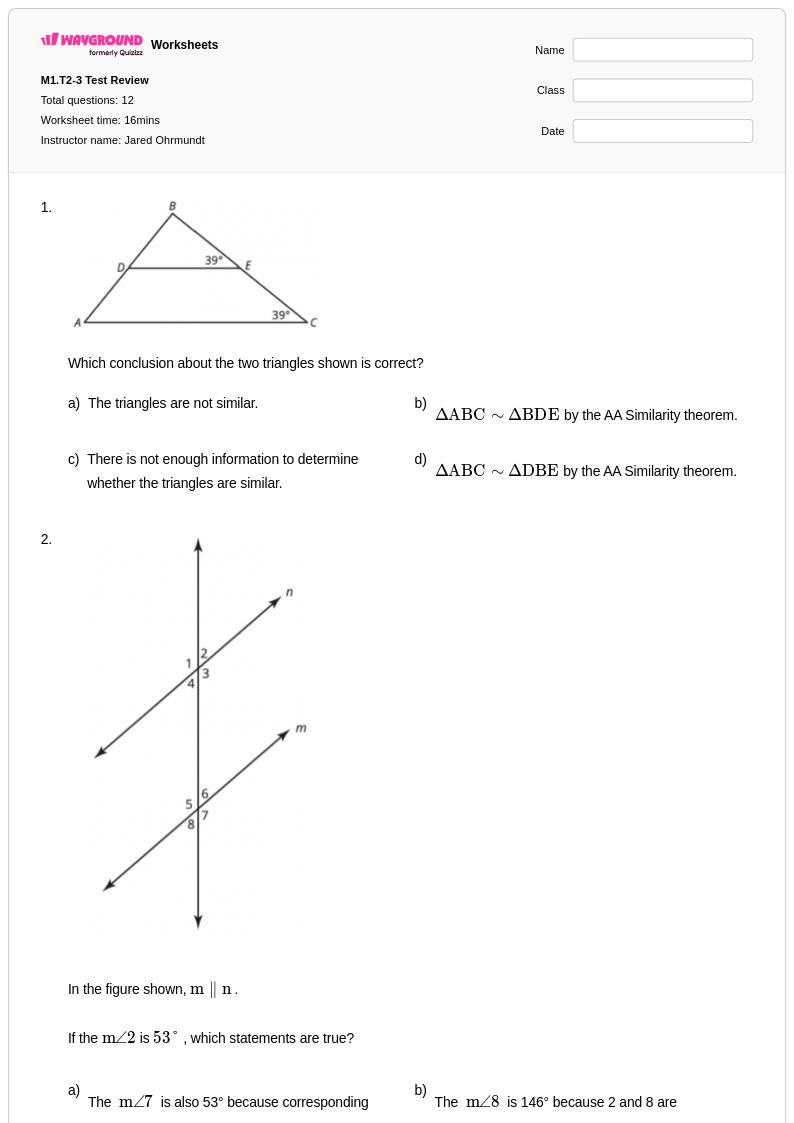
12 คิว
8th
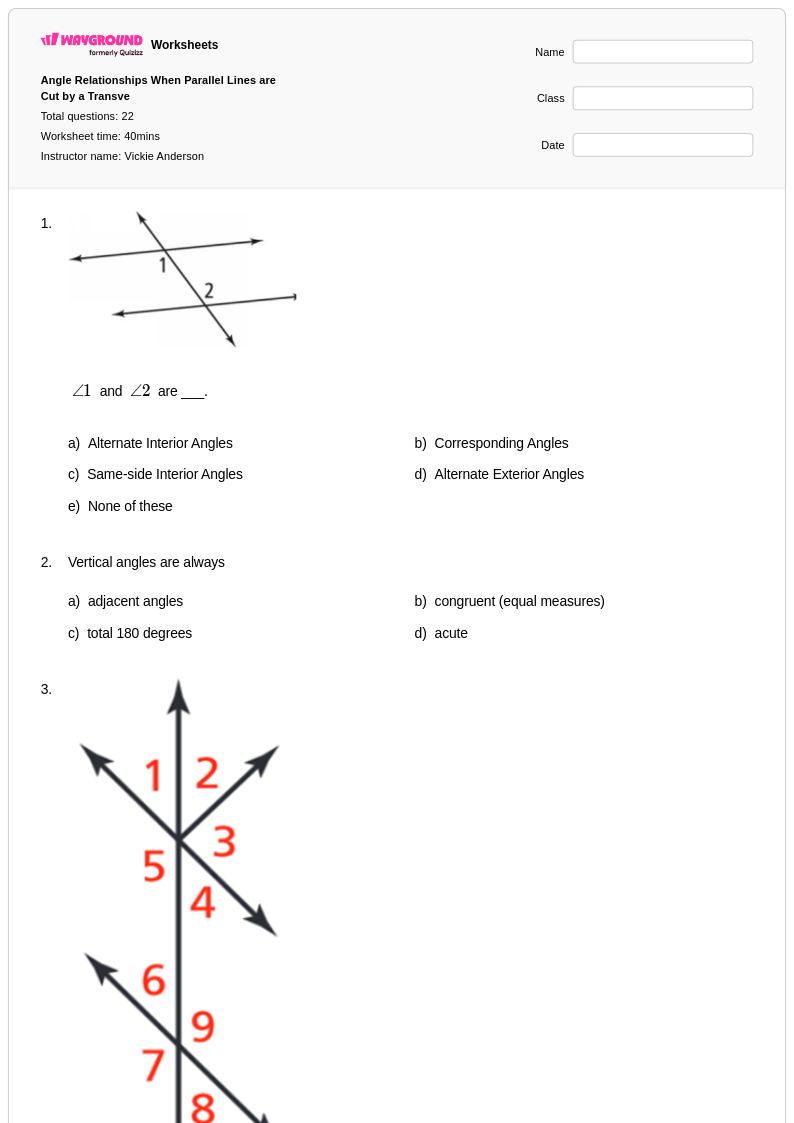
22 คิว
8th

36 คิว
8th - 10th

12 คิว
8th
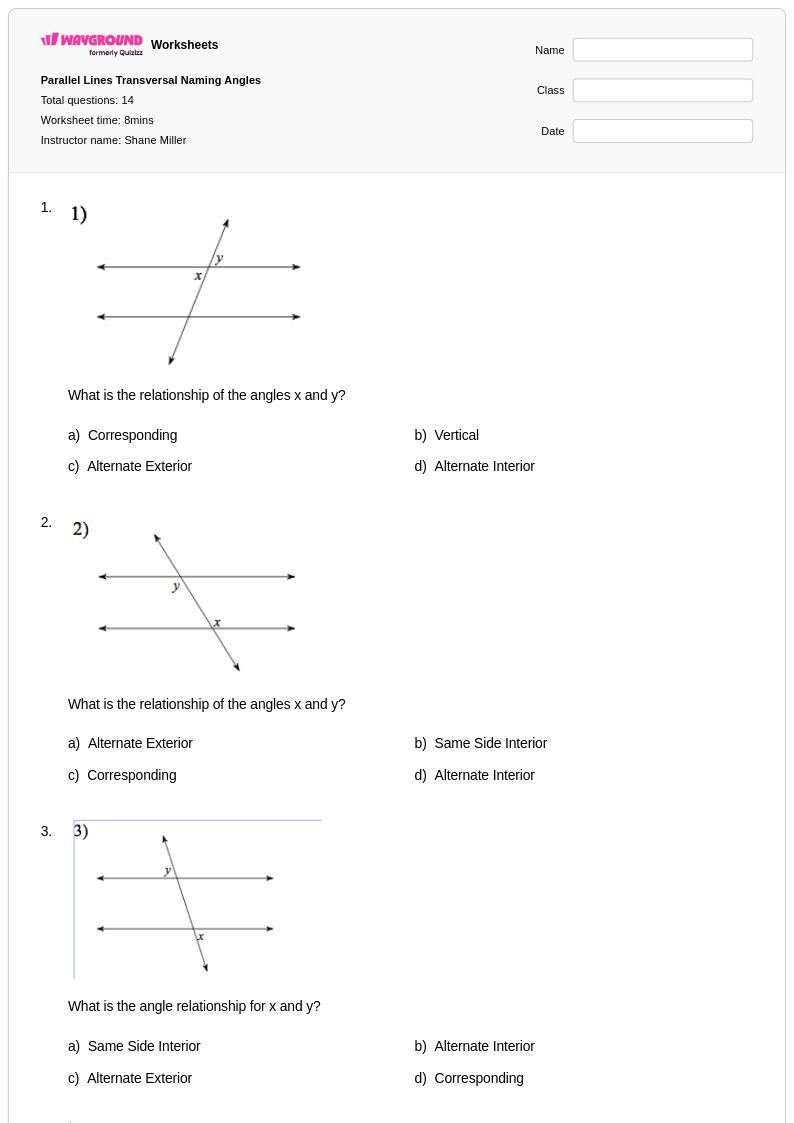
14 คิว
7th - 10th
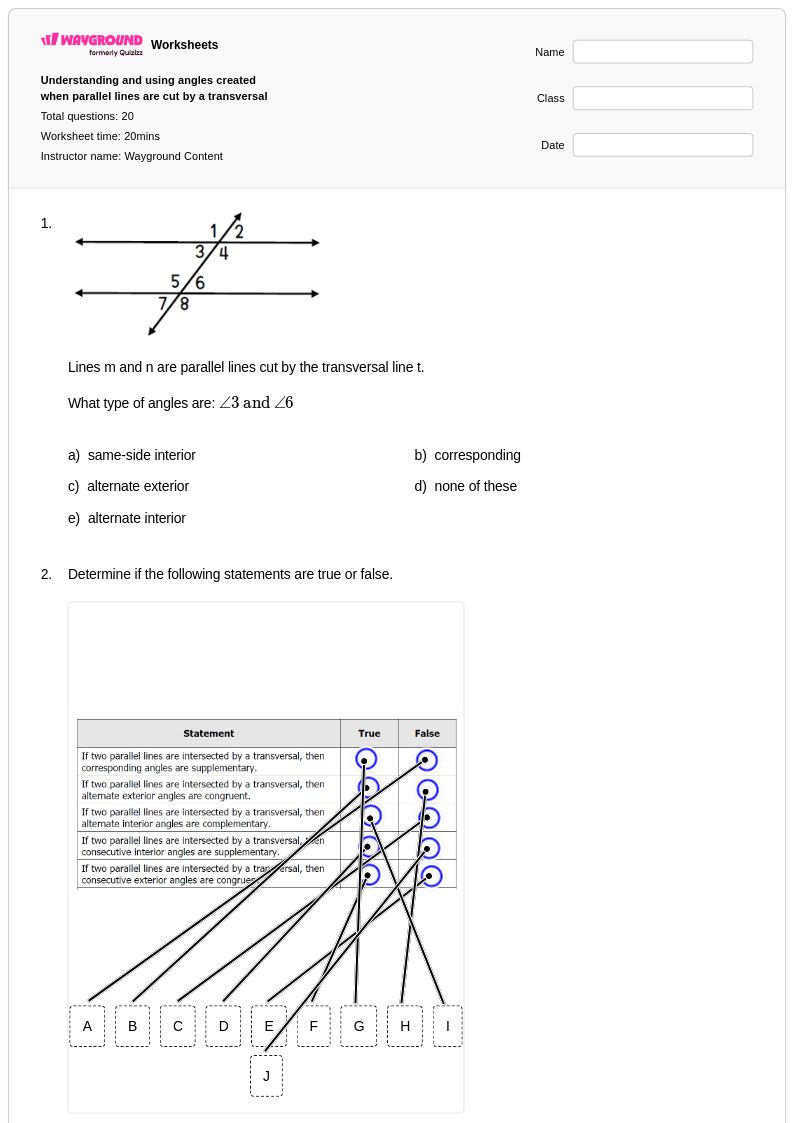
20 คิว
8th
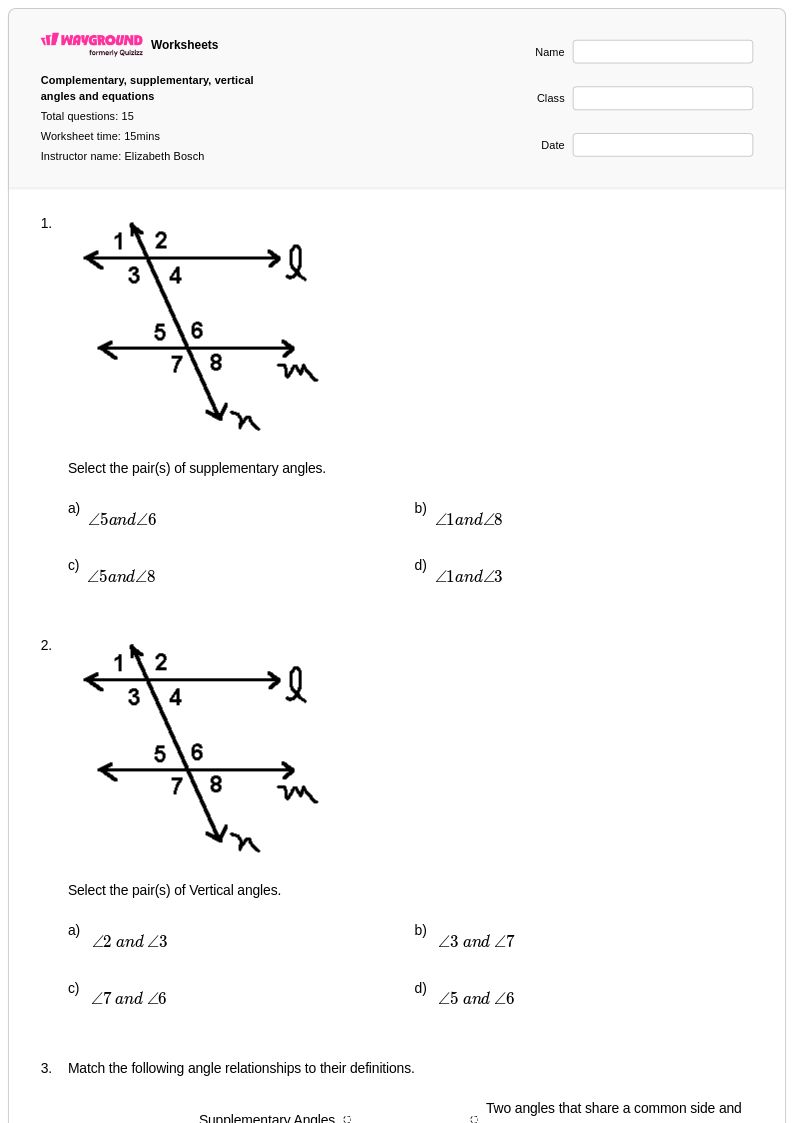
15 คิว
7th - Uni

20 คิว
8th

16 คิว
8th
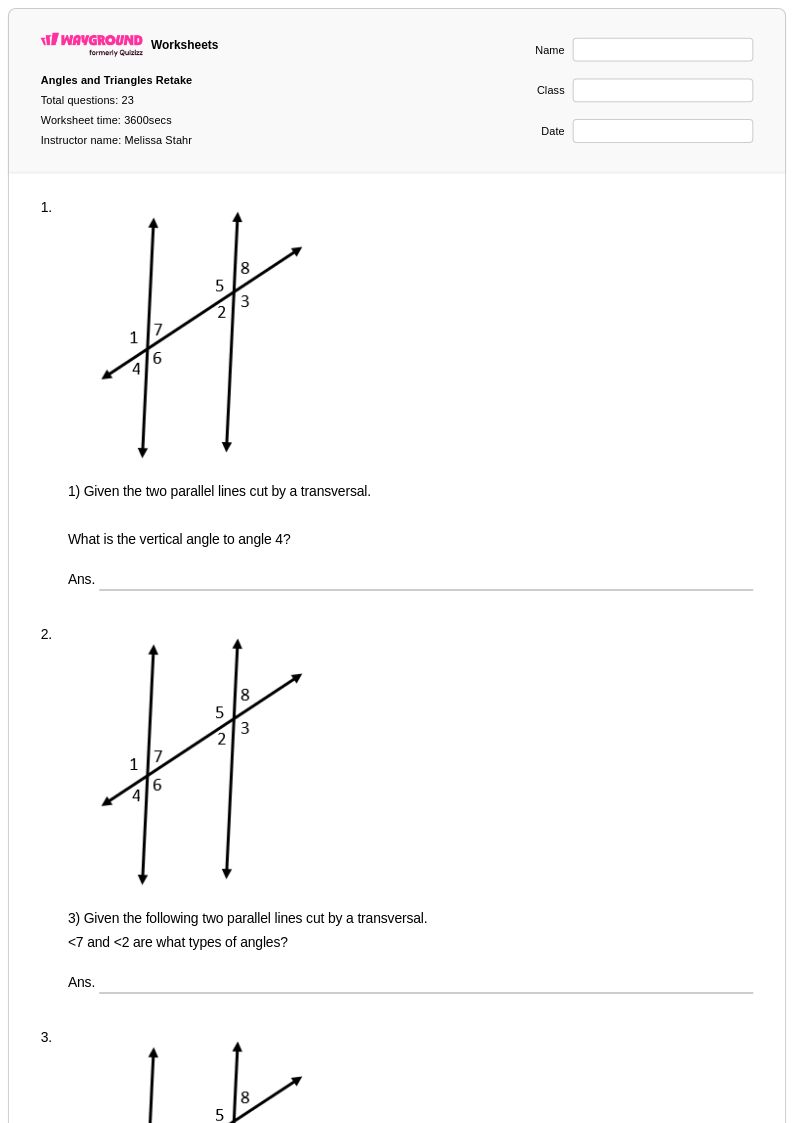
23 คิว
8th
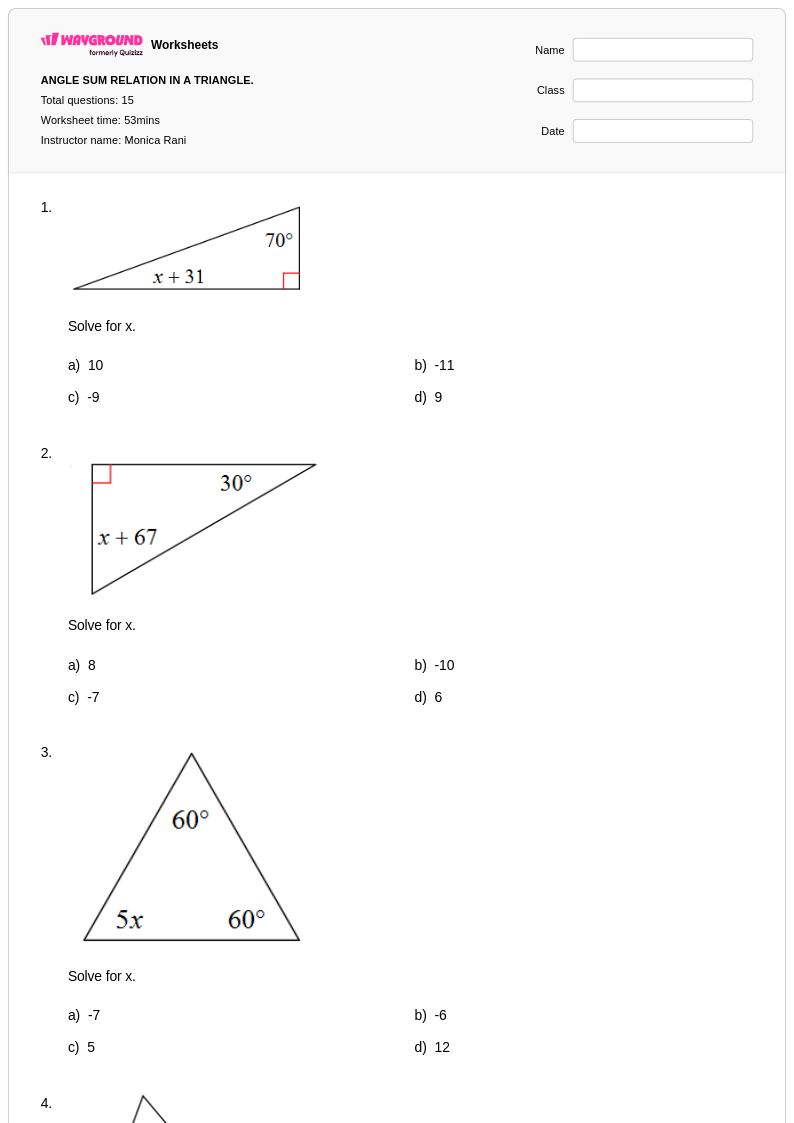
15 คิว
8th

10 คิว
8th

10 คิว
8th

10 คิว
8th
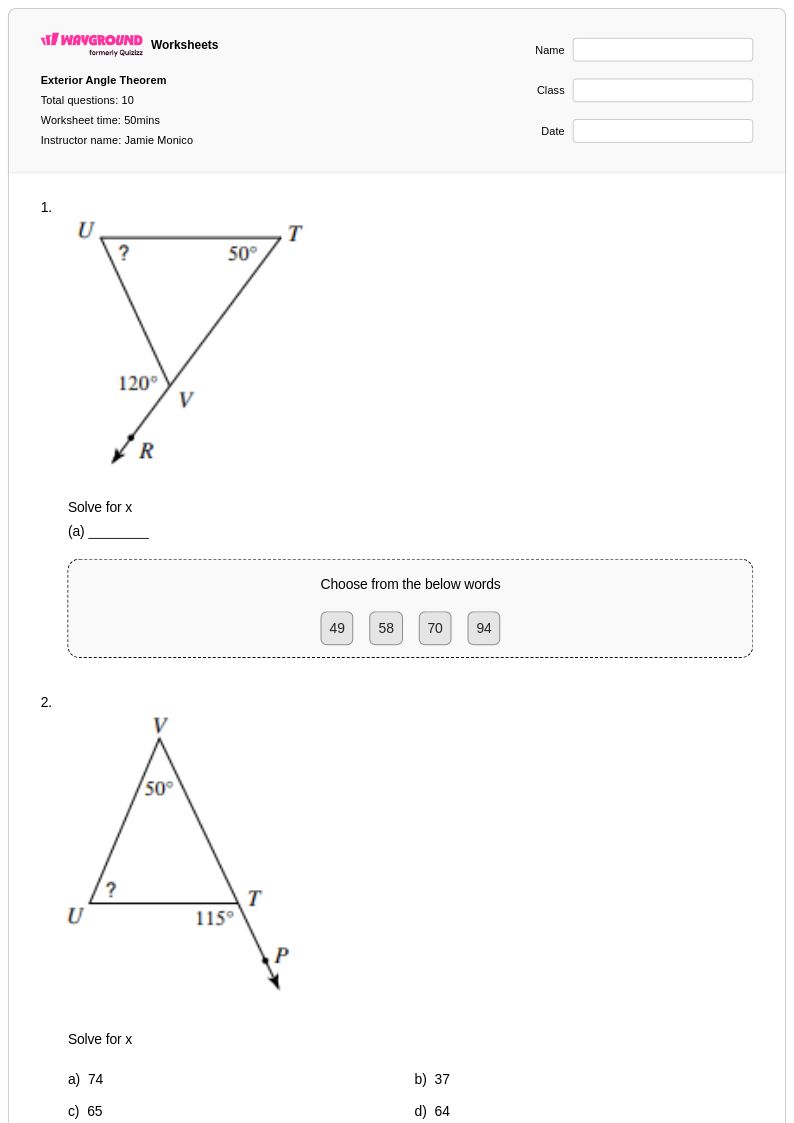
10 คิว
8th
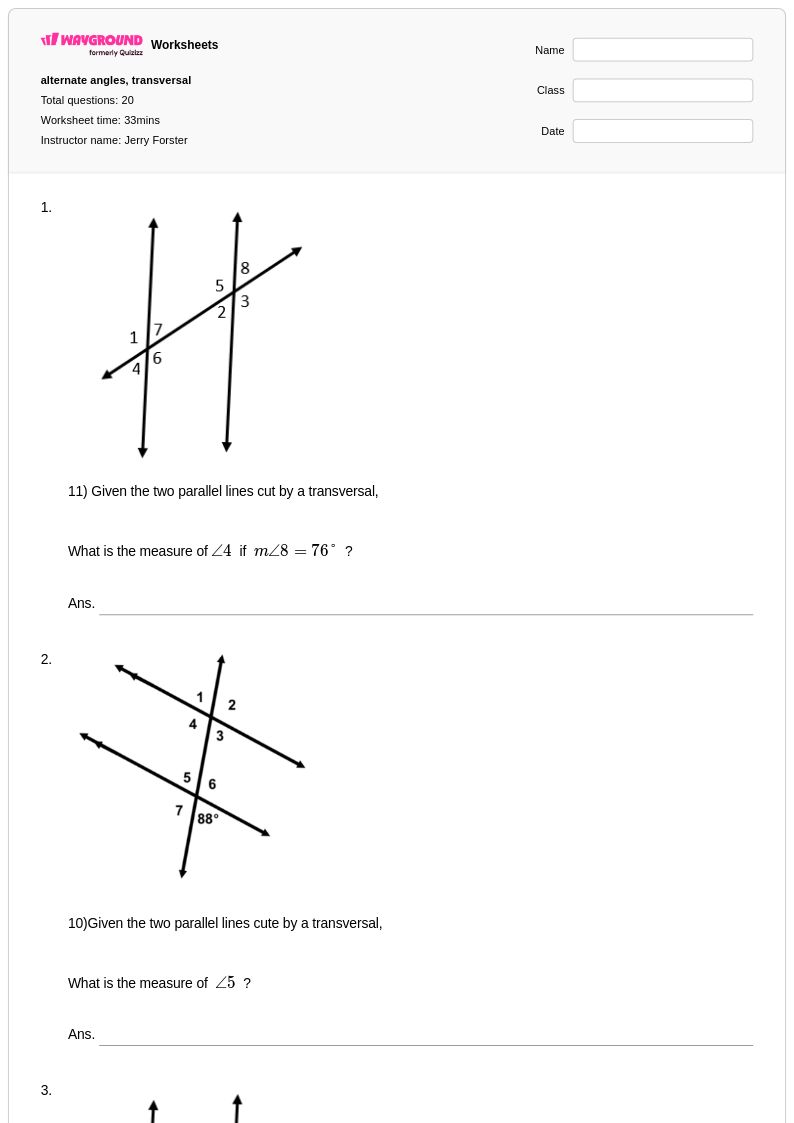
20 คิว
8th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 8
สำรวจแผ่นงาน ทฤษฎีบทผลรวมมุมของรูปหลายเหลี่ยม ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 8
แบบฝึกหัดทฤษฎีบทผลรวมมุมภายในของรูปหลายเหลี่ยมสำหรับนักเรียนชั้น ม.2 มอบโอกาสในการฝึกฝนอย่างครอบคลุมเพื่อให้นักเรียนเชี่ยวชาญหลักการพื้นฐานอย่างหนึ่งของเรขาคณิต แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยให้นักเรียนเข้าใจว่าผลรวมของมุมภายในในรูปหลายเหลี่ยมใดๆ เท่ากับ (n-2) × 180° โดยที่ n แทนจำนวนด้าน ผ่านแบบฝึกหัดที่มีโครงสร้าง นักเรียนจะพัฒนาความชำนาญในการคำนวณมุมที่หายไป การระบุประเภทของรูปหลายเหลี่ยมตามขนาดของมุม และการประยุกต์ใช้ทฤษฎีบทเพื่อแก้ปัญหาทางเรขาคณิตในโลกแห่งความเป็นจริง ชุดแบบฝึกหัดที่ครอบคลุมของ Wayground ประกอบด้วยแบบฝึกหัดพร้อมเฉลยคำตอบโดยละเอียด แหล่งข้อมูล PDF ที่พิมพ์ได้ฟรี และชุดปัญหาที่หลากหลายซึ่งค่อยๆ สร้างความมั่นใจให้กับนักเรียนในการทำงานกับรูปหลายเหลี่ยมตั้งแต่รูปสามเหลี่ยมไปจนถึงรูปหลายด้านที่ซับซ้อน
Wayground ซึ่งเดิมชื่อ Quizizz ช่วยเสริมศักยภาพให้กับครูผู้สอนด้วยแหล่งข้อมูลทฤษฎีบทผลรวมมุมภายในของรูปหลายเหลี่ยมที่สร้างโดยครูผู้สอนนับล้านรายการ ซึ่งช่วยให้การวางแผนบทเรียนและการสอนที่แตกต่างกันมีประสิทธิภาพยิ่งขึ้น แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพ ช่วยให้ครูสามารถค้นหาสื่อการเรียนการสอนที่สอดคล้องกับมาตรฐานและวัตถุประสงค์การเรียนรู้ที่เฉพาะเจาะจงได้อย่างรวดเร็ว ในขณะที่เครื่องมือปรับแต่งช่วยให้สามารถแก้ไขแบบฝึกหัดที่มีอยู่ให้ตรงกับความต้องการที่หลากหลายของห้องเรียนได้ แหล่งข้อมูลอเนกประสงค์เหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่สามารถพิมพ์ได้ และเวอร์ชันดิจิทัลแบบโต้ตอบ ซึ่งสนับสนุนการใช้งานที่ยืดหยุ่นไม่ว่าจะเป็นการสอนทั้งชั้นเรียน การทำงานกลุ่มเล็ก หรือการฝึกฝนด้วยตนเอง ครูสามารถใช้สื่อเหล่านี้ได้อย่างมีประสิทธิภาพสำหรับการแนะนำแนวคิดเบื้องต้น การแก้ไขปัญหาเฉพาะจุดสำหรับนักเรียนที่ประสบปัญหา กิจกรรมเสริมสำหรับผู้เรียนที่มีความสามารถสูง และการเสริมสร้างทักษะอย่างต่อเนื่องตลอดหลักสูตรเรขาคณิตระดับชั้น ม.2
