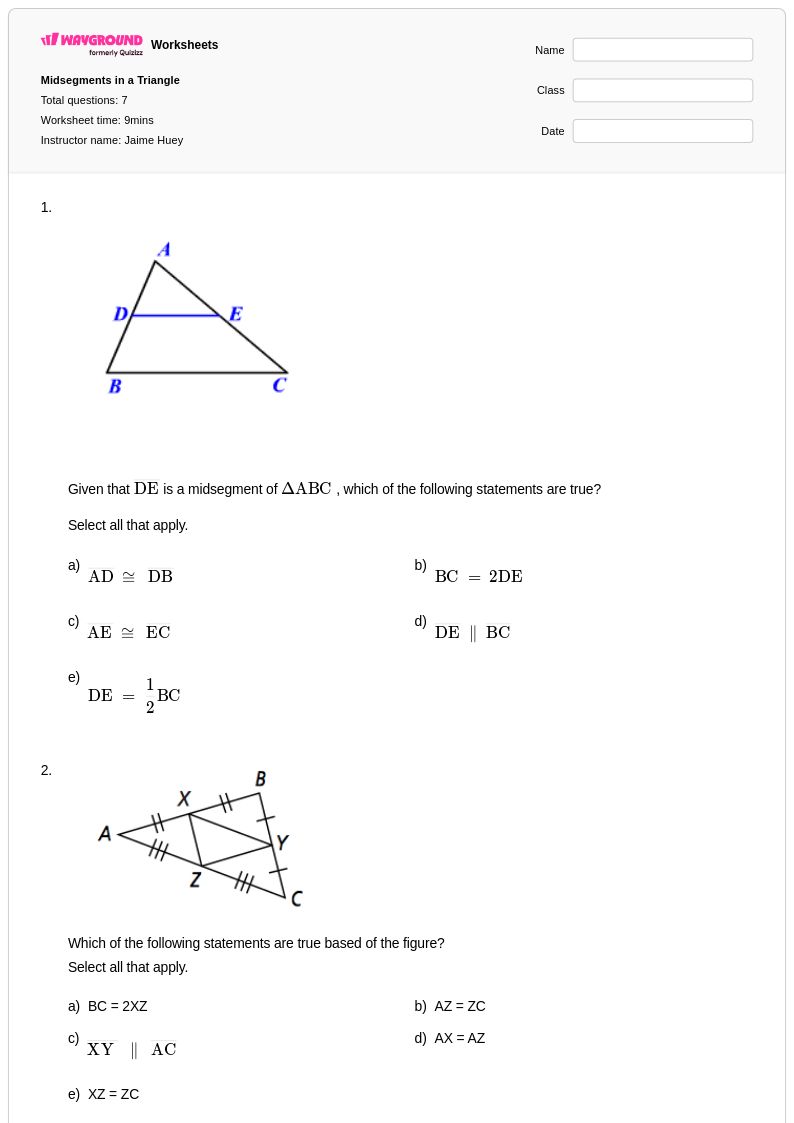
7 คิว
9th - 12th

26 คิว
10th

22 คิว
9th
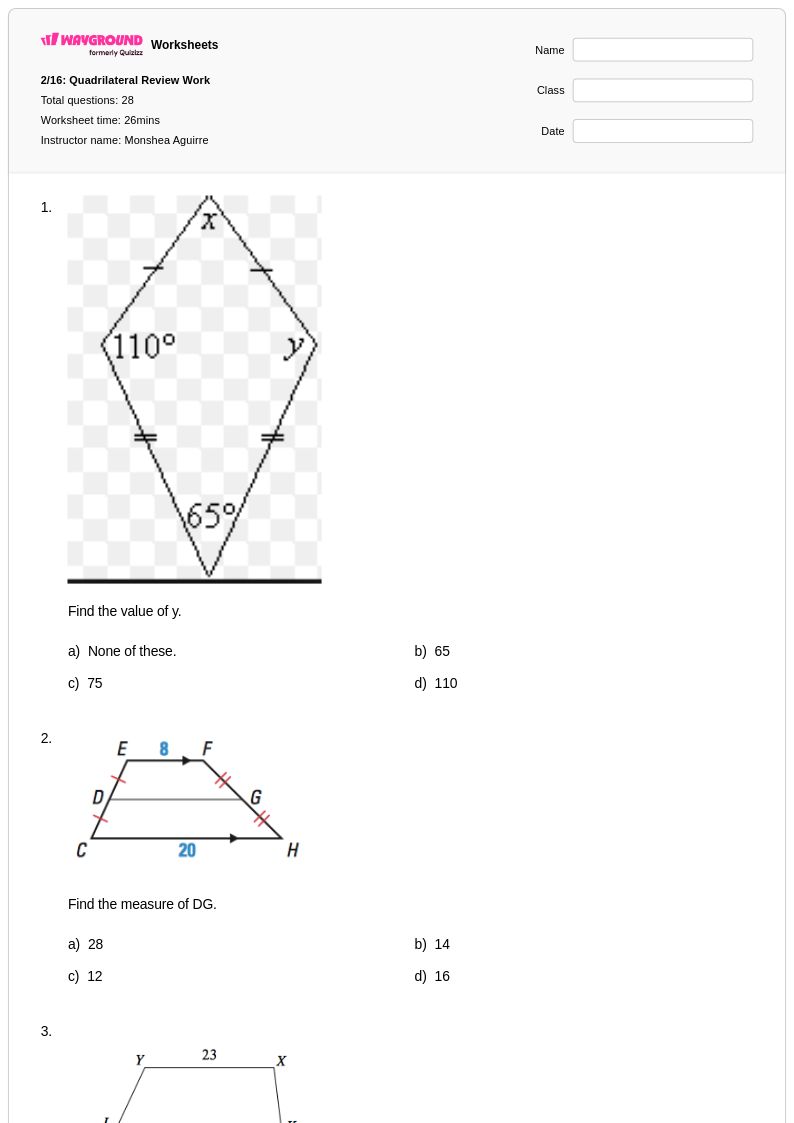
28 คิว
9th - 12th

100 คิว
9th - 12th

437 คิว
9th - 12th
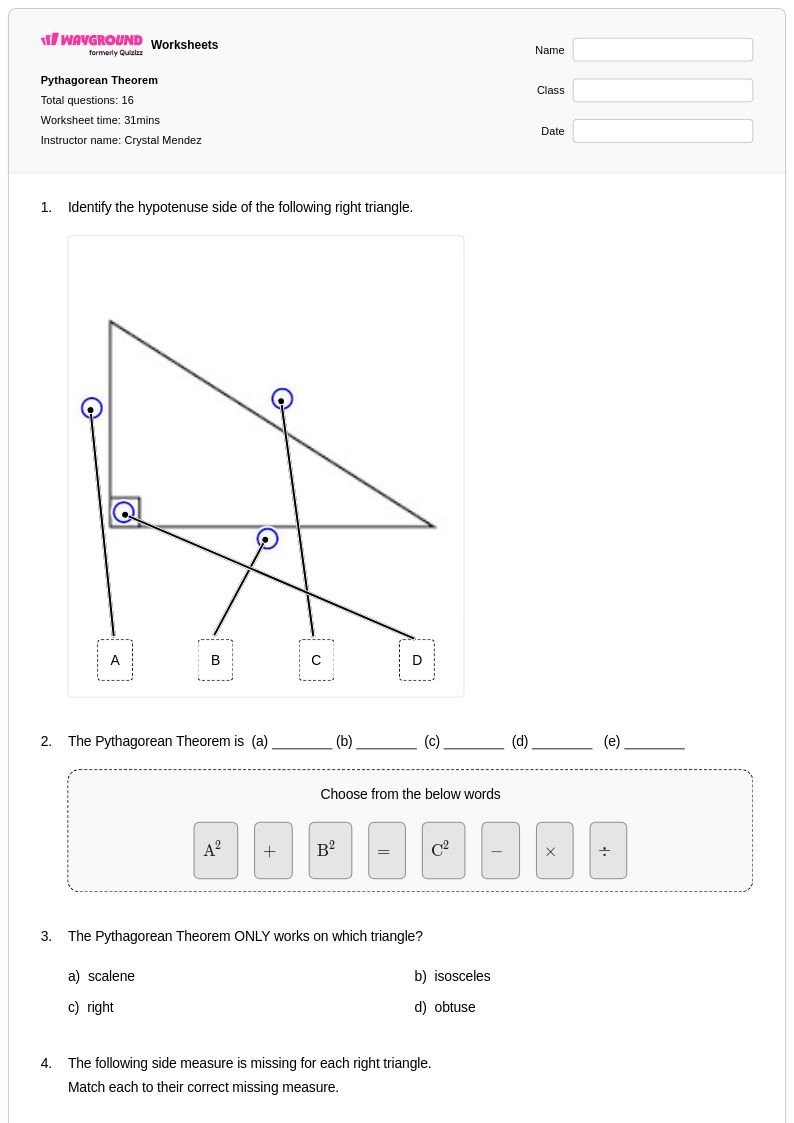
16 คิว
10th
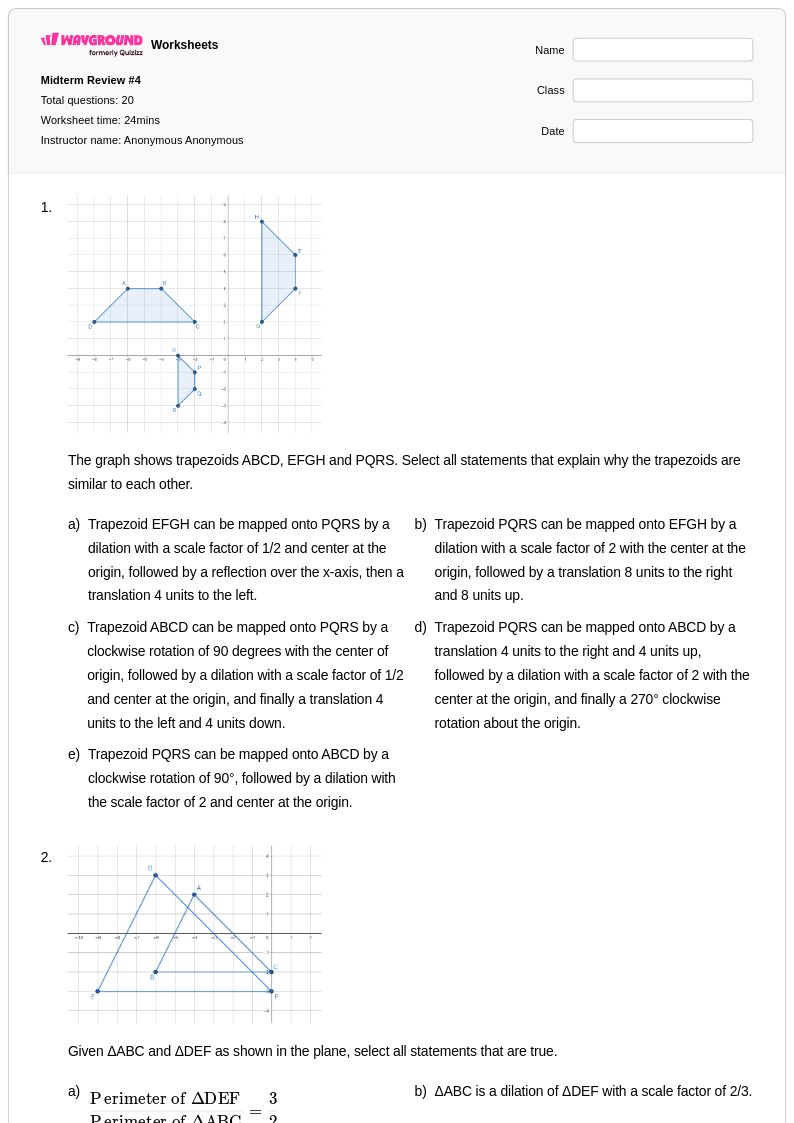
20 คิว
10th
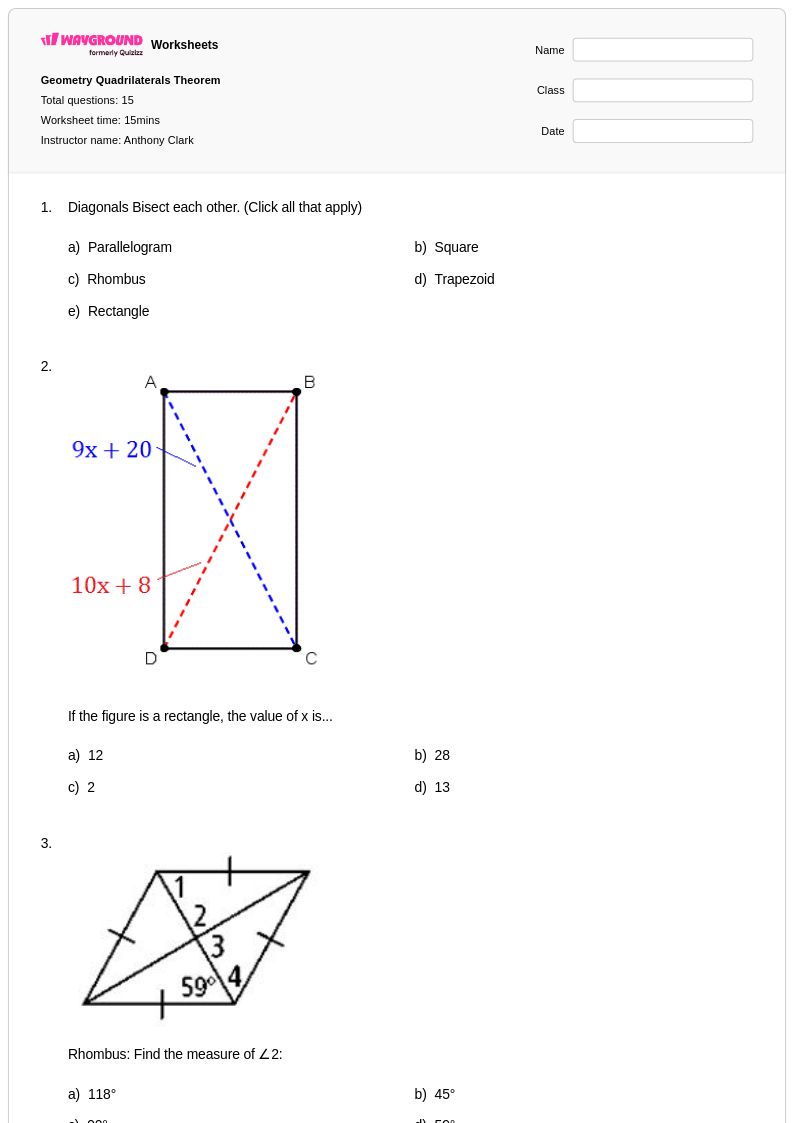
15 คิว
10th - Uni
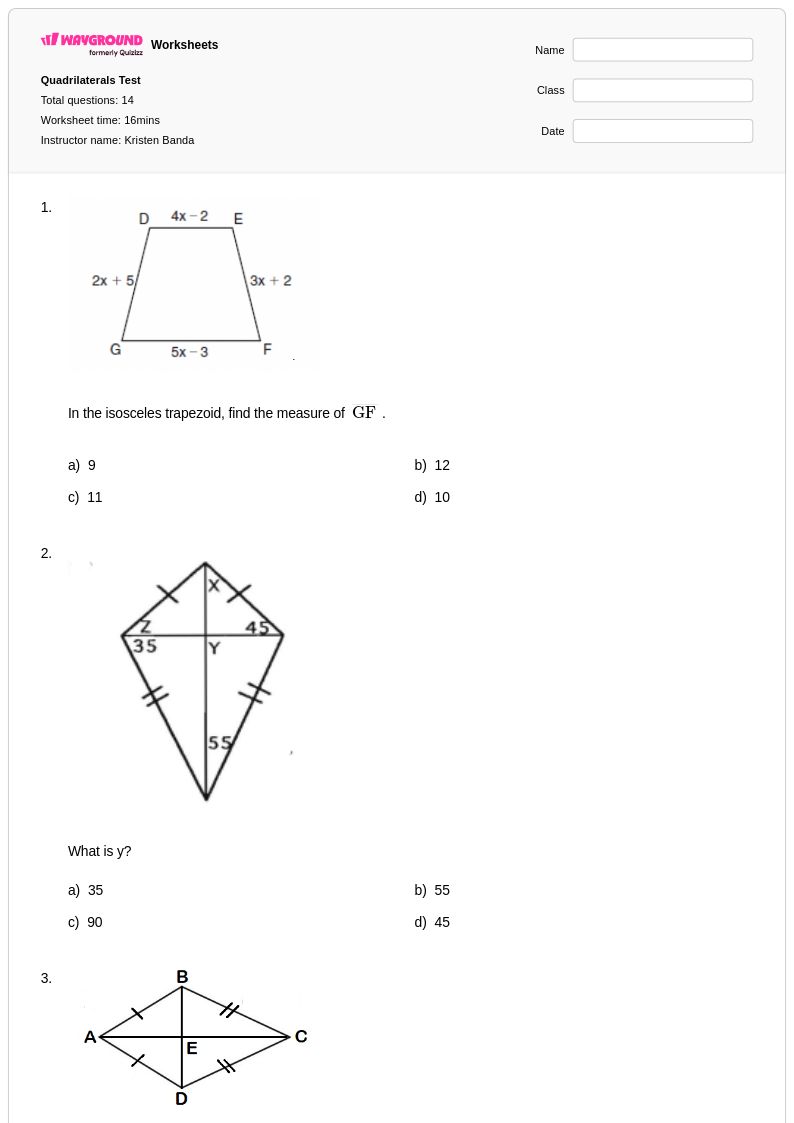
14 คิว
10th

50 คิว
10th

35 คิว
8th - 10th
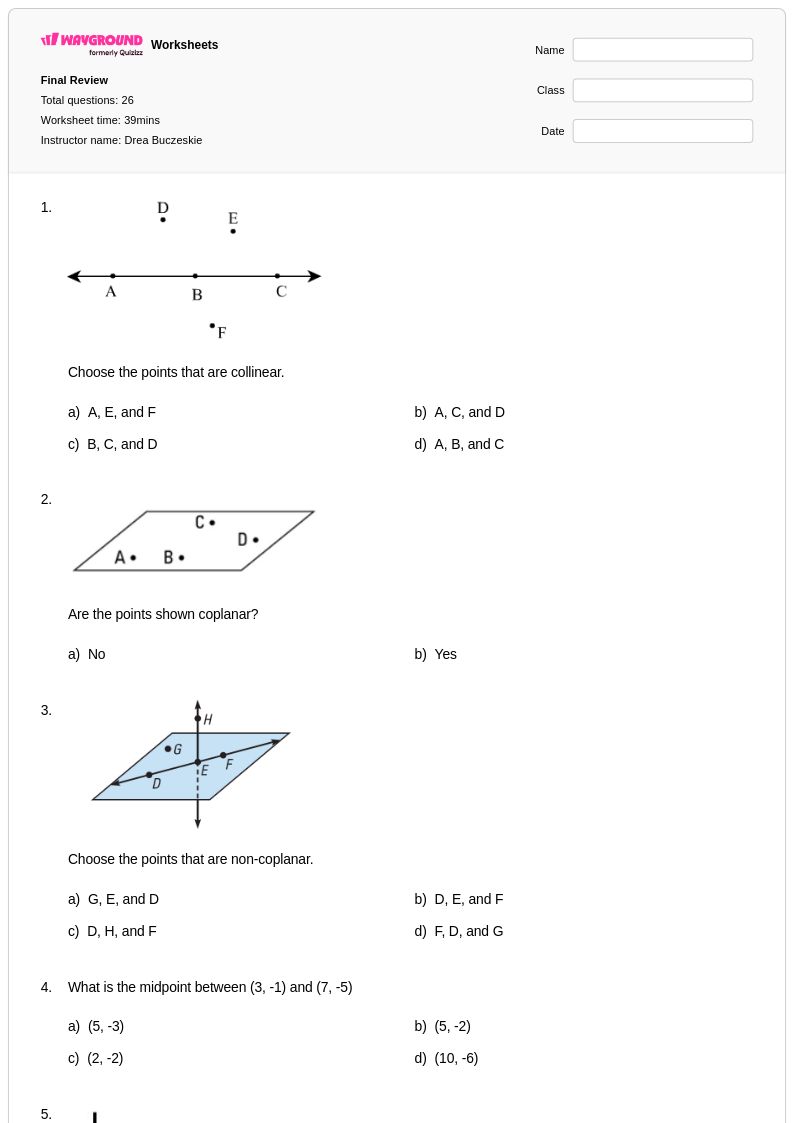
26 คิว
9th - 12th
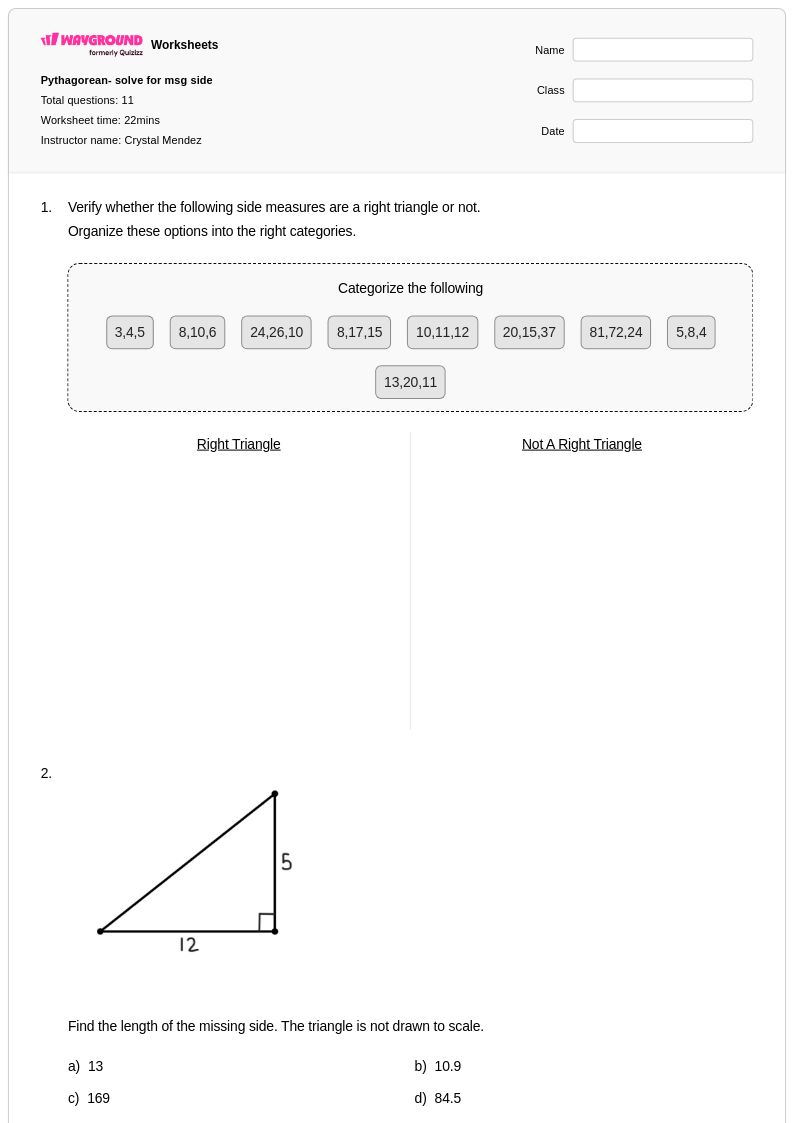
11 คิว
10th
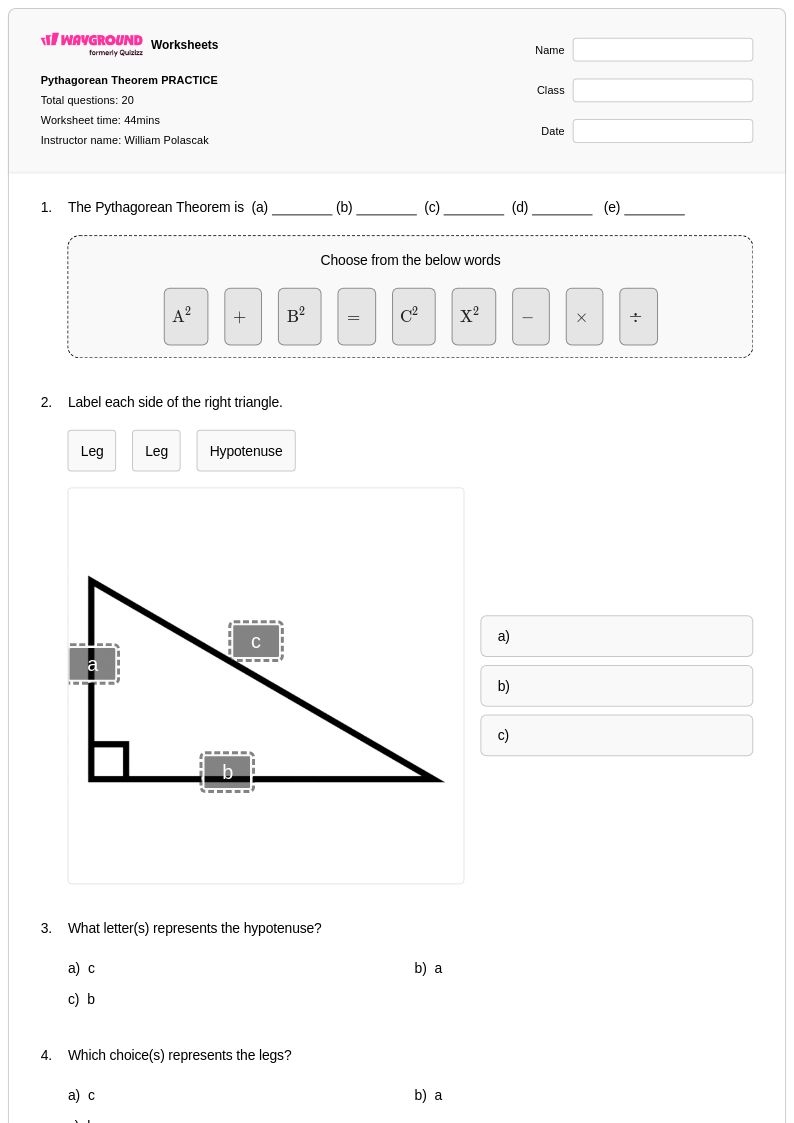
20 คิว
9th
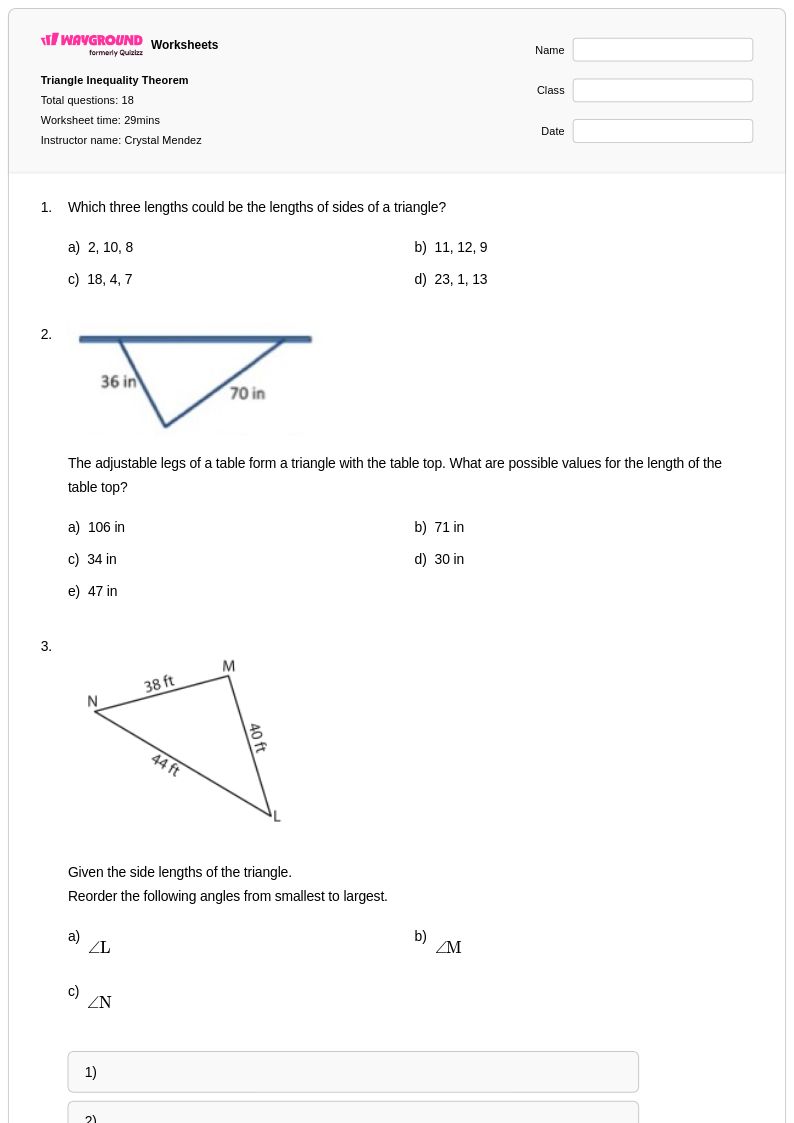
18 คิว
10th
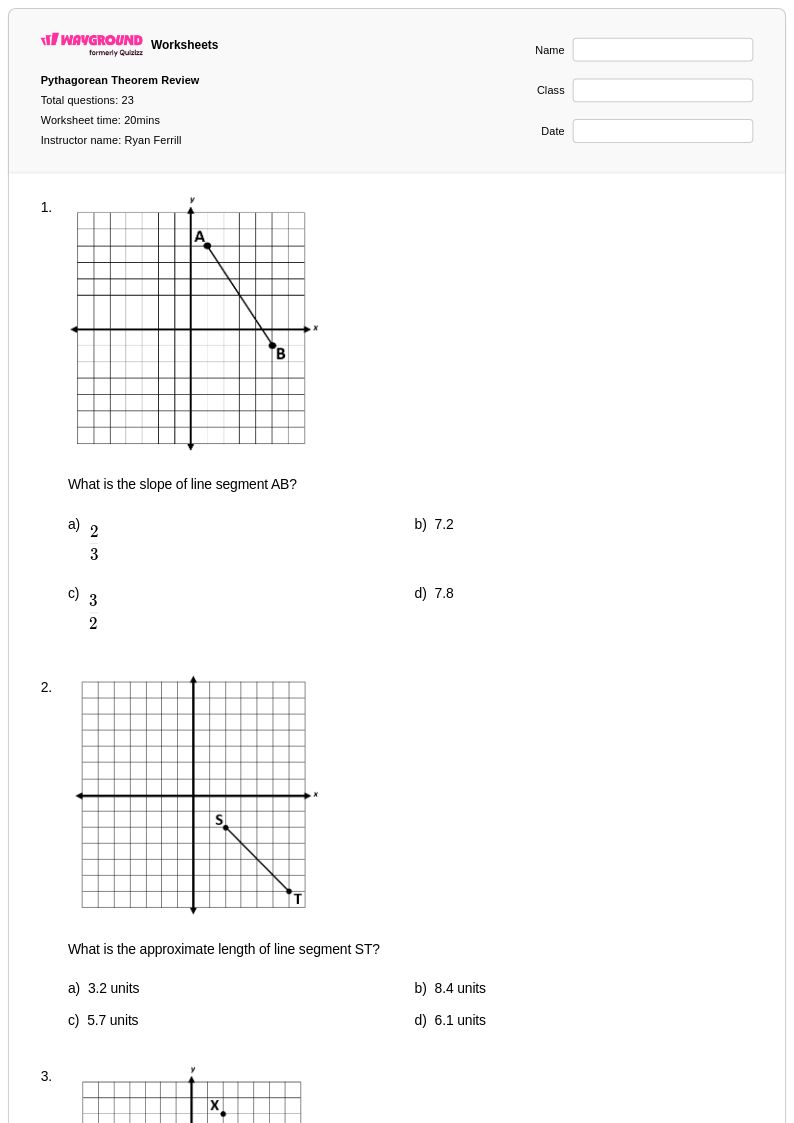
23 คิว
8th

18 คิว
9th - Uni
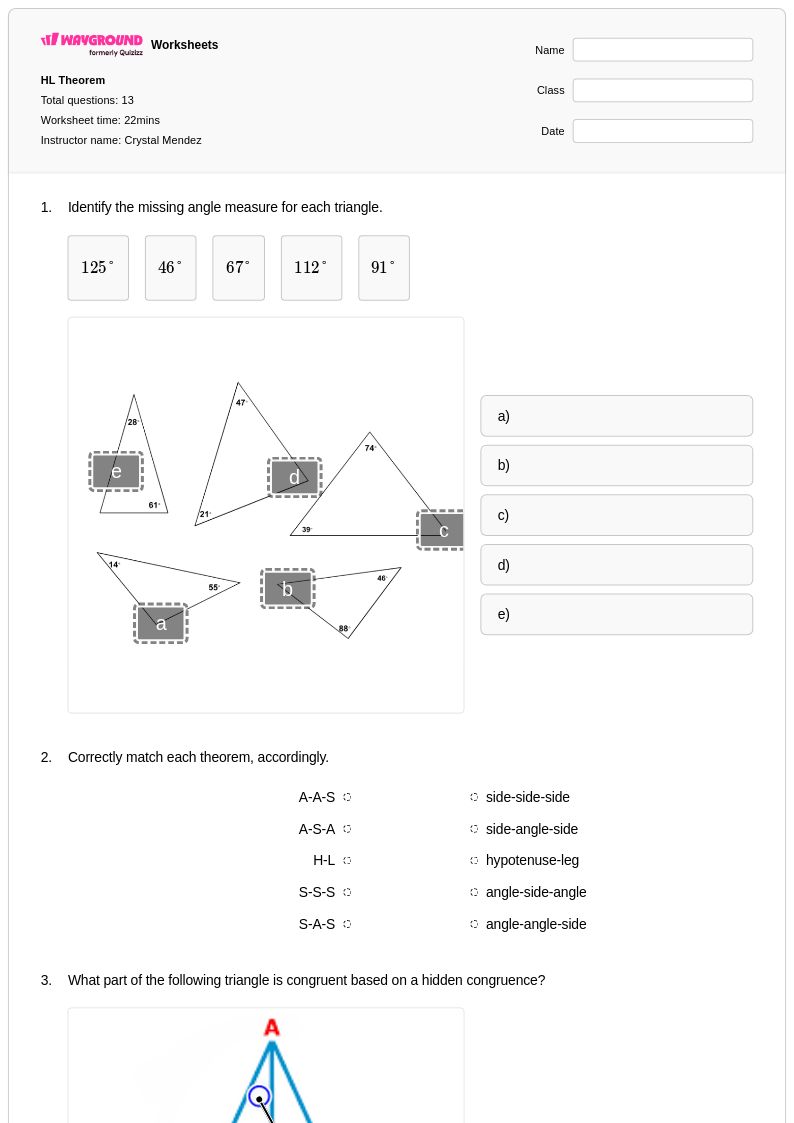
13 คิว
10th
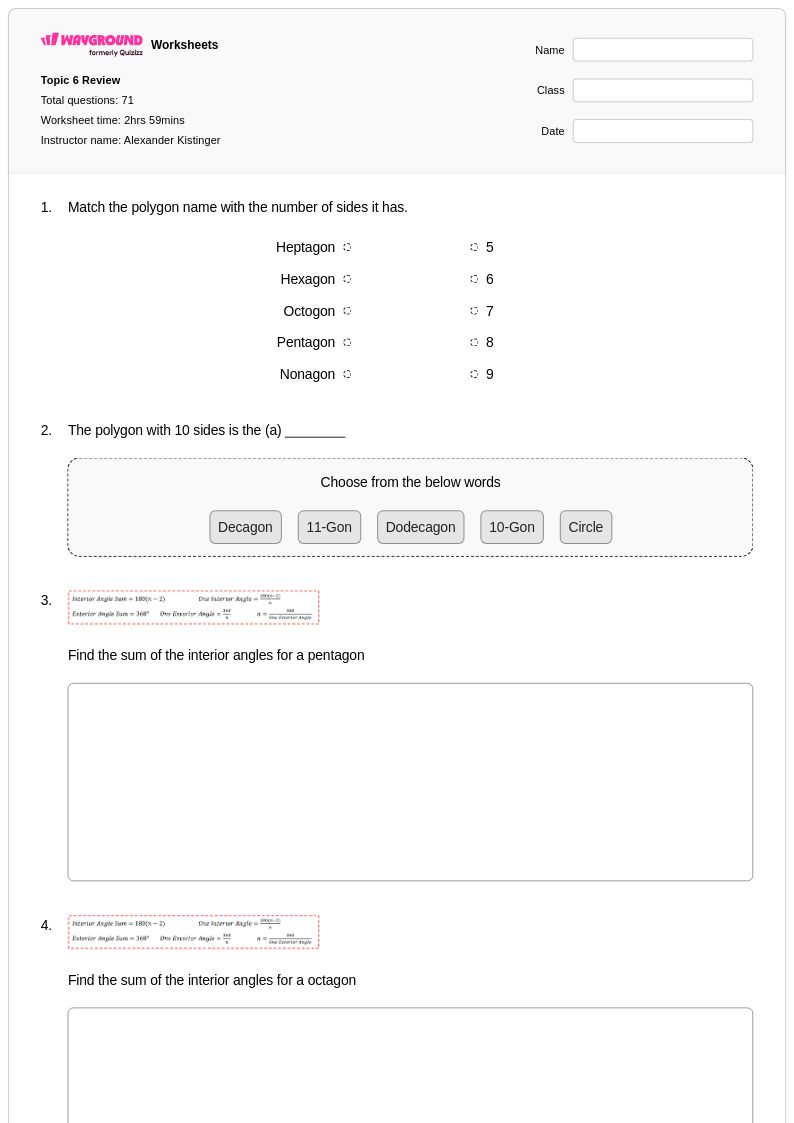
71 คิว
10th
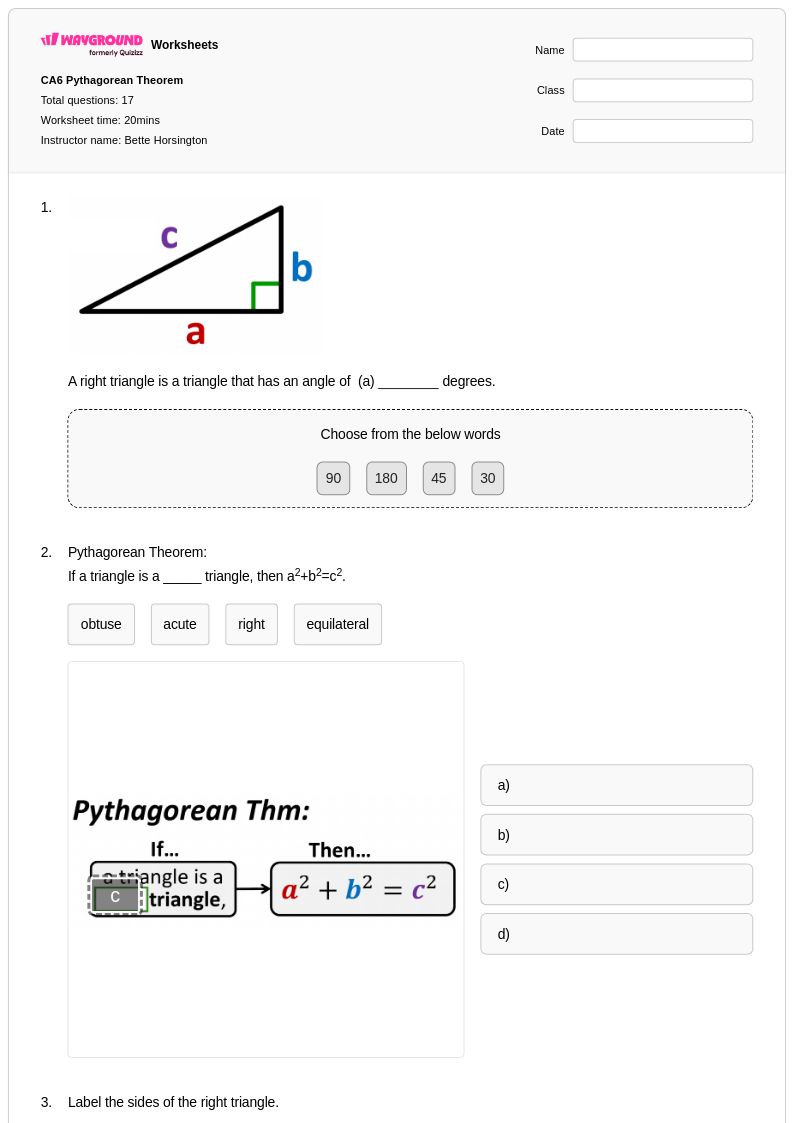
17 คิว
8th - Uni
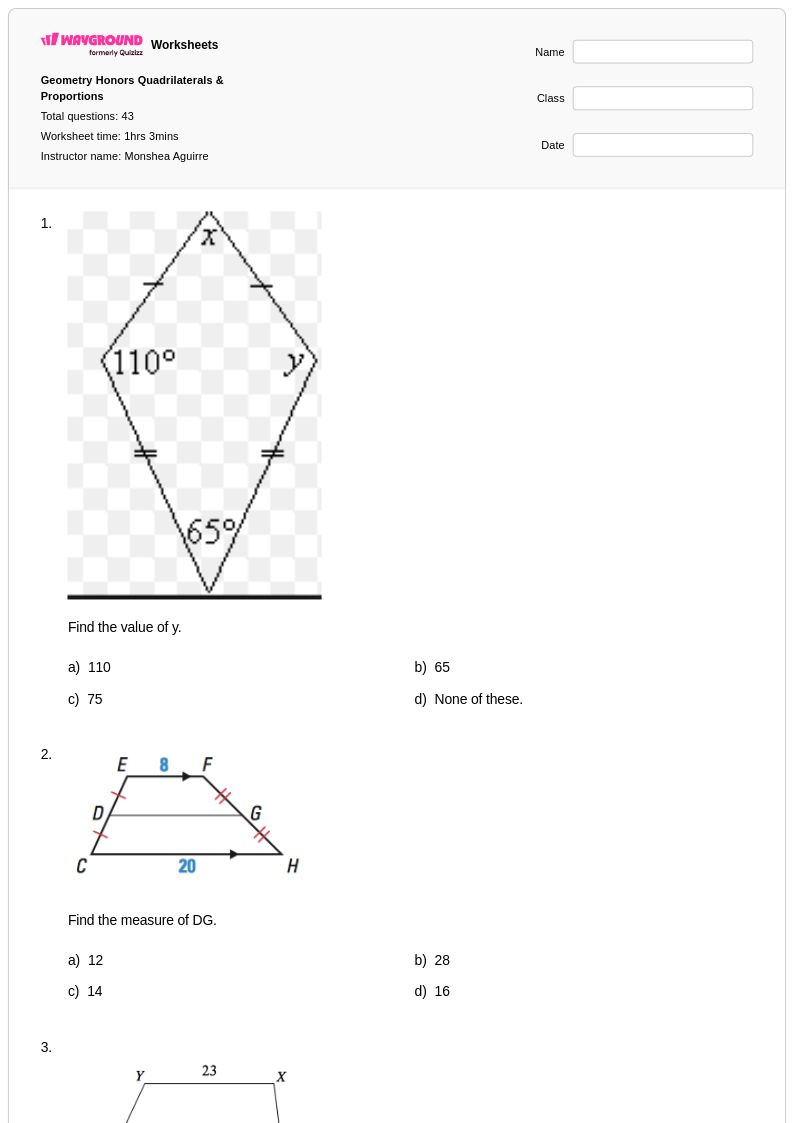
43 คิว
9th - 12th

29 คิว
9th - 12th

70 คิว
10th
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน ทฤษฎีบทส่วนกลางรูปสี่เหลี่ยมคางหมู ที่พิมพ์ได้
ทฤษฎีบทเส้นกึ่งกลางของรูปสี่เหลี่ยมคางหมูเป็นแนวคิดพื้นฐานในเรขาคณิตที่นักเรียนต้องเชี่ยวชาญเพื่อทำความเข้าใจคุณสมบัติและความสัมพันธ์ภายในรูปสี่เหลี่ยม Wayground มีแบบฝึกหัดทฤษฎีบทเส้นกึ่งกลางของรูปสี่เหลี่ยมคางหมูที่ครอบคลุม ซึ่งมีโจทย์ฝึกฝนที่ตรงเป้าหมายเพื่อเสริมสร้างหลักการทางเรขาคณิตที่สำคัญนี้ ซึ่งกล่าวว่าเส้นกึ่งกลางของรูปสี่เหลี่ยมคางหมูขนานกับฐานทั้งสองและมีความยาวเท่ากับค่าเฉลี่ยของความยาวฐาน แหล่งข้อมูลที่พิมพ์ได้ฟรีเหล่านี้มีแบบฝึกหัดหลากหลาย ตั้งแต่การคำนวณเส้นกึ่งกลางพื้นฐานไปจนถึงการประยุกต์ใช้ที่ซับซ้อนมากขึ้นซึ่งเกี่ยวข้องกับเรขาคณิตพิกัดและนิพจน์พีชคณิต แบบฝึกหัดแต่ละแผ่นมาพร้อมกับเฉลยคำตอบโดยละเอียด ช่วยให้นักเรียนตรวจสอบงานของตนเองและระบุจุดที่ต้องปรับปรุง พร้อมทั้งสร้างความมั่นใจในการประยุกต์ใช้ทฤษฎีบทกับปัญหาประเภทต่างๆ
คลังข้อมูลขนาดใหญ่ของ Wayground ซึ่งมีแหล่งข้อมูลที่สร้างโดยครูหลายล้านรายการ ช่วยให้ครูผู้สอนสามารถสนับสนุนการเรียนรู้ของนักเรียนได้อย่างมีประสิทธิภาพผ่านสื่อทฤษฎีบทเส้นกึ่งกลางของรูปสี่เหลี่ยมคางหมูที่คัดสรรมาอย่างดี แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานหลักสูตรเฉพาะได้อย่างรวดเร็ว และสามารถปรับการสอนให้เหมาะสมกับความต้องการของนักเรียนแต่ละคนได้ ไม่ว่าจะอยู่ในรูปแบบไฟล์ PDF แบบดั้งเดิมสำหรับการแจกจ่ายในห้องเรียน หรือเข้าถึงผ่านแพลตฟอร์มดิจิทัลสำหรับการเรียนรู้ทางไกล ทรัพยากรที่ปรับแต่งได้เหล่านี้ให้ความยืดหยุ่นสำหรับสภาพแวดล้อมการสอนที่หลากหลาย ครูสามารถบูรณาการสื่อเหล่านี้เข้ากับการวางแผนบทเรียนได้อย่างราบรื่น ไม่ว่าจะเป็นการสอนเบื้องต้น การแก้ไขปัญหาเฉพาะหน้าสำหรับผู้เรียนที่มีปัญหา หรือกิจกรรมเสริมสำหรับนักเรียนที่มีความสามารถสูง เพื่อให้มั่นใจว่าผู้เรียนทุกคนจะมีความเข้าใจอย่างถ่องแท้ว่าทฤษฎีบทส่วนกลางของรูปสี่เหลี่ยมคางหมูสามารถนำไปใช้กับสถานการณ์การแก้ปัญหาทางเรขาคณิตในโลกแห่งความเป็นจริงได้อย่างไร
