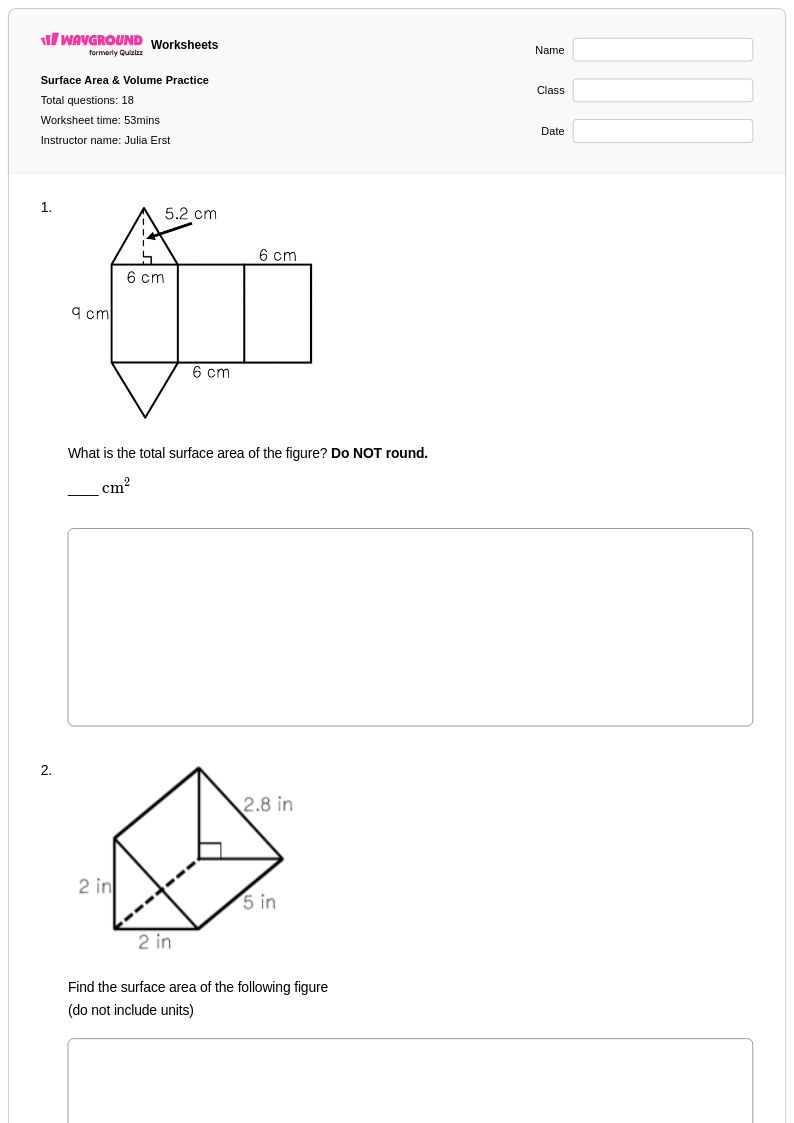
18 คิว
7th

19 คิว
8th

25 คิว
11th

17 คิว
5th
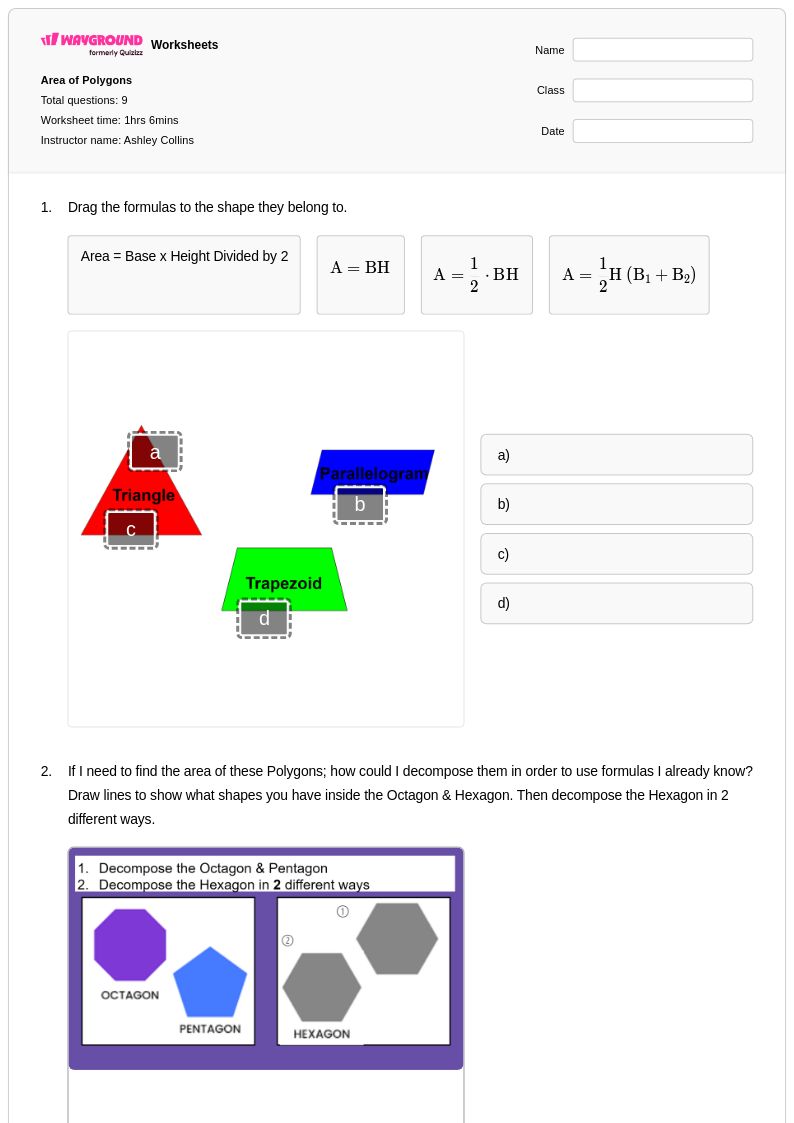
16 คิว
6th

12 คิว
6th
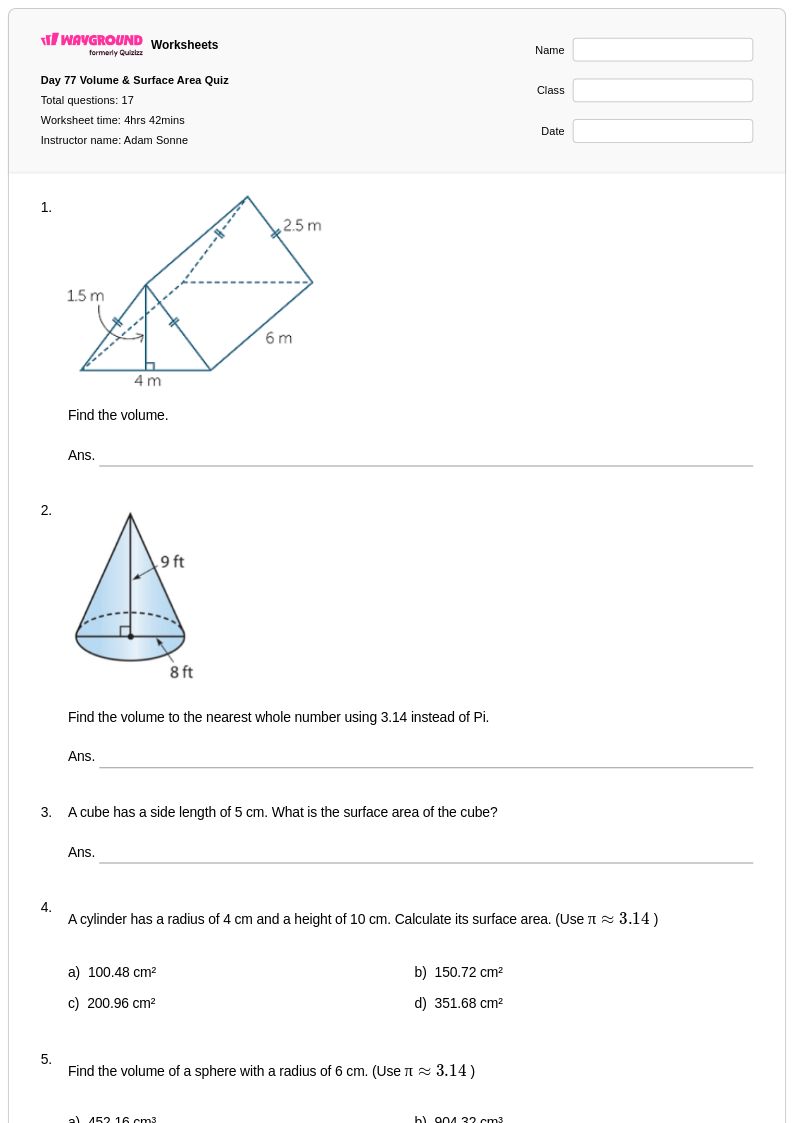
17 คิว
10th
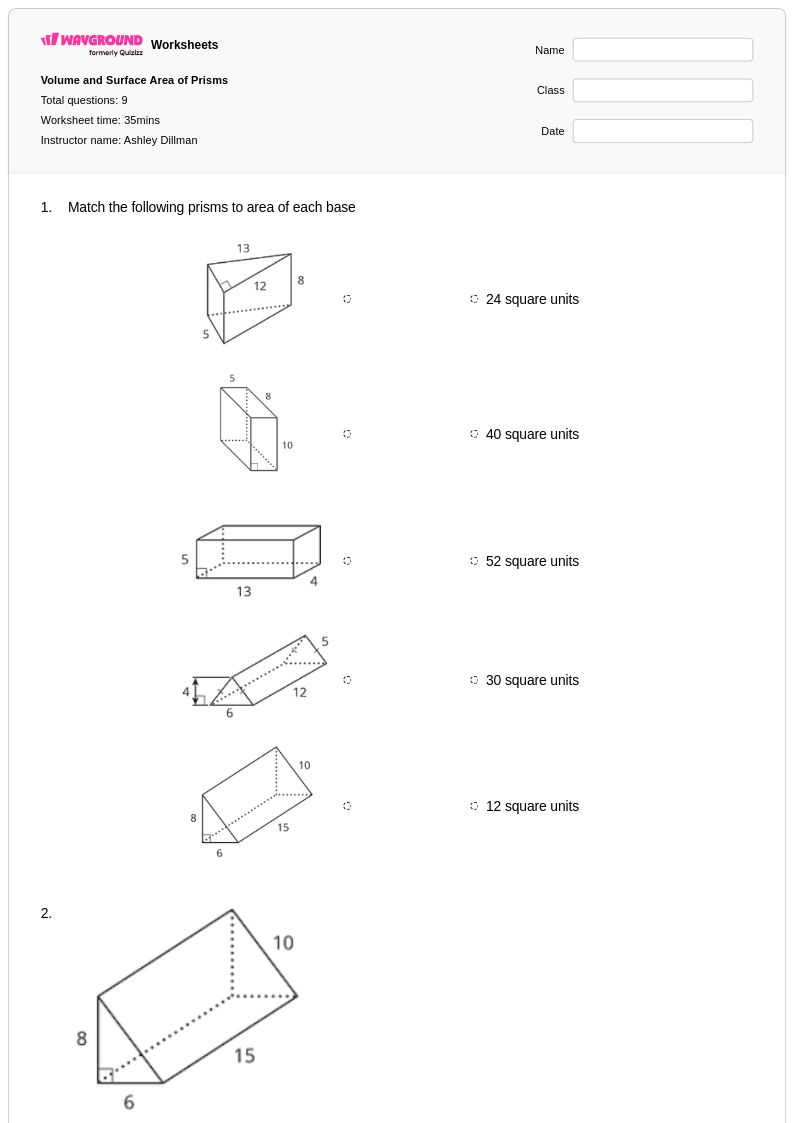
9 คิว
7th

15 คิว
7th

10 คิว
8th

40 คิว
9th - 12th

20 คิว
9th - 12th

16 คิว
10th

13 คิว
5th - 7th

14 คิว
10th - Uni

16 คิว
6th
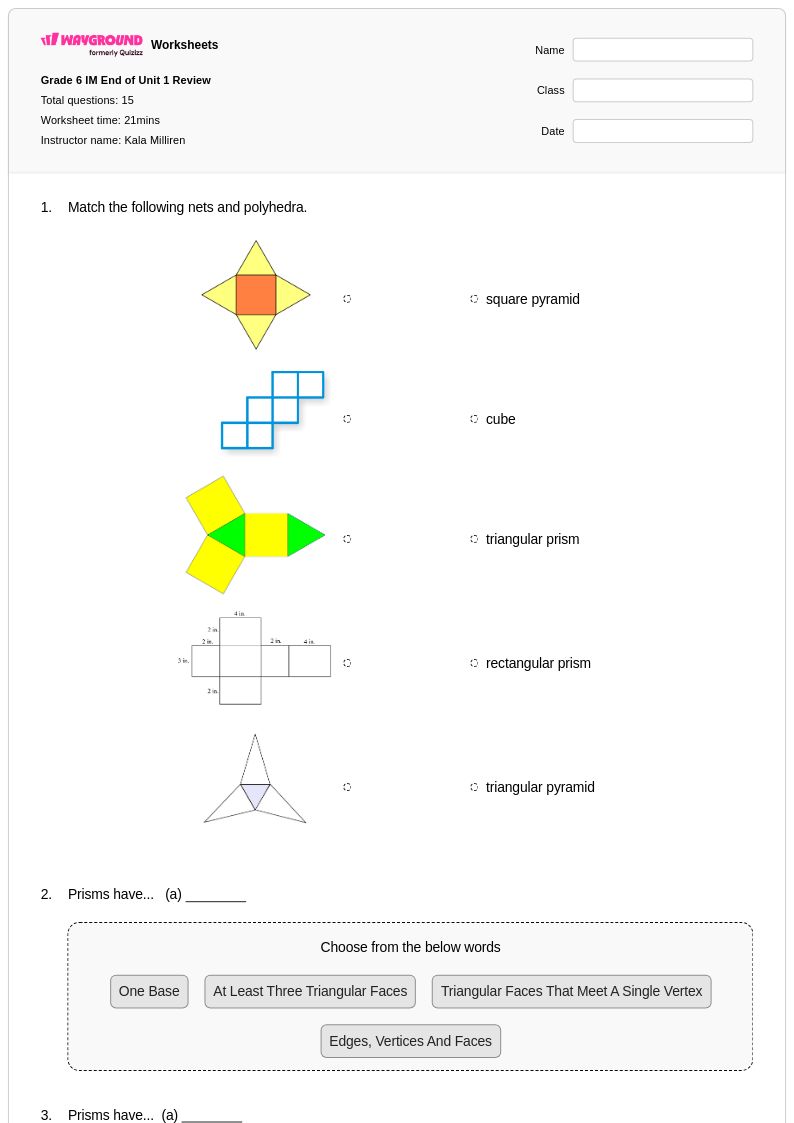
15 คิว
6th
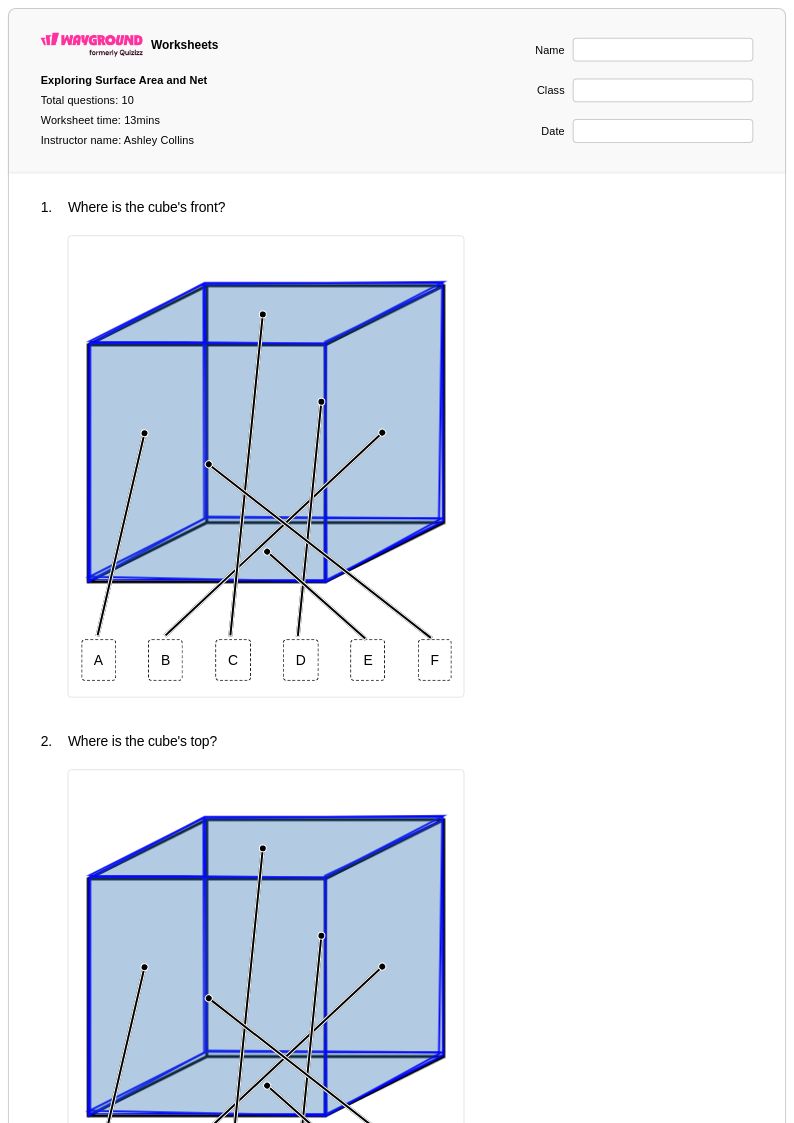
10 คิว
6th
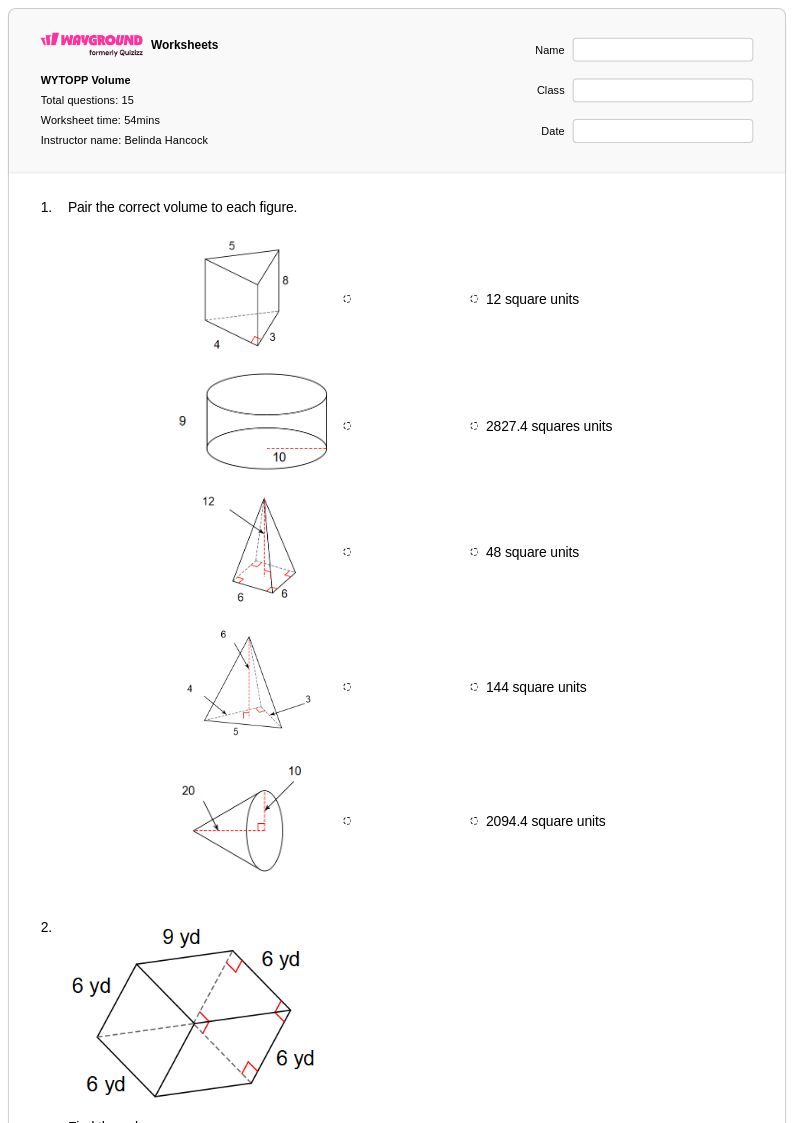
15 คิว
10th
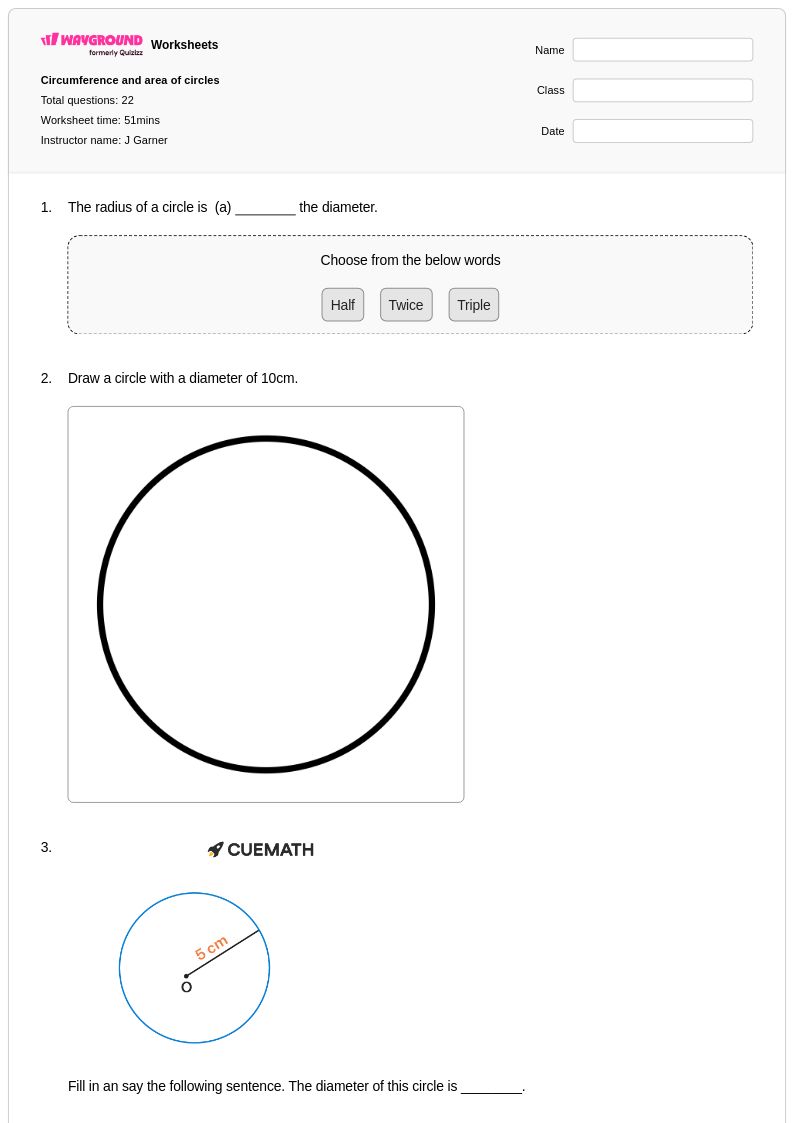
22 คิว
7th
14 คิว
6th

10 คิว
8th

20 คิว
8th - Uni
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน ปริมาตรและพื้นที่ผิวของกรวย ที่พิมพ์ได้
แบบฝึกหัดเรื่องปริมาตรและพื้นที่ผิวของกรวยจาก Wayground (เดิมคือ Quizizz) เป็นแบบฝึกหัดที่ครอบคลุมสำหรับนักเรียนที่กำลังเรียนรู้การคำนวณค่าสามมิติที่สำคัญเหล่านี้ แบบฝึกหัดที่ออกแบบมาอย่างพิถีพิถันนี้ช่วยเสริมสร้างทักษะทางเรขาคณิตที่สำคัญ รวมถึงการใช้สูตรปริมาตรของกรวย (V = 1/3πr²h) การคำนวณพื้นที่ผิวข้างและพื้นที่ผิวทั้งหมดโดยใช้สูตรที่เหมาะสม และการแก้ปัญหาหลายขั้นตอนที่เกี่ยวข้องกับการใช้งานกรวยในชีวิตจริง นักเรียนจะได้ฝึกฝนโจทย์ปัญหาที่ค่อยๆ ยากขึ้น ตั้งแต่การใช้สูตรพื้นฐานไปจนถึงสถานการณ์ที่ซับซ้อนซึ่งต้องใช้การวิเคราะห์มิติและการแปลงหน่วย แบบฝึกหัดแต่ละแผ่นมีเฉลยคำตอบโดยละเอียดที่สนับสนุนการเรียนรู้ด้วยตนเองและการประเมินตนเอง ในขณะที่รูปแบบที่พิมพ์ได้ฟรีช่วยให้เข้าถึงได้ทั้งสำหรับการเรียนการสอนในห้องเรียนและการบ้าน แหล่งข้อมูล PDF เหล่านี้ช่วยสร้างความเข้าใจเชิงแนวคิดอย่างเป็นระบบว่ารัศมี ความสูง และความสูงเอียงมีความสัมพันธ์กับการวัดกรวยอย่างไร เตรียมความพร้อมให้นักเรียนสำหรับการแก้ปัญหาทางเรขาคณิตขั้นสูง
Wayground (เดิมชื่อ Quizizz) สนับสนุนครูคณิตศาสตร์ด้วยแหล่งข้อมูลที่สร้างโดยครูหลายล้านรายการ โดยเน้นเฉพาะเรื่องปริมาตรและพื้นที่ผิวของกรวย มีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพเพื่อค้นหาสื่อที่สอดคล้องกับมาตรฐานหลักสูตรและวัตถุประสงค์การเรียนรู้ได้อย่างสมบูรณ์แบบ เครื่องมือการปรับระดับความยากง่ายของแพลตฟอร์มช่วยให้ครูสามารถปรับแต่งแบบฝึกหัดสำหรับระดับทักษะที่แตกต่างกัน ตั้งแต่แนวคิดพื้นฐานเกี่ยวกับกรวยไปจนถึงการประยุกต์ใช้ขั้นสูงที่เกี่ยวข้องกับรูปทรงผสมและปัญหาการหาค่าเหมาะสมที่สุด ครูสามารถเข้าถึงทั้งรูปแบบที่พิมพ์ได้และดิจิทัลได้อย่างราบรื่น รวมถึงเวอร์ชัน PDF ที่ดาวน์โหลดได้ ทำให้การวางแผนบทเรียนมีประสิทธิภาพในขณะที่รองรับเทคโนโลยีในห้องเรียนที่หลากหลายและวิธีการเรียนรู้ที่แตกต่างกัน ชุดแบบฝึกหัดที่ครอบคลุมเหล่านี้ช่วยอำนวยความสะดวกในการฝึกฝนทักษะที่ตรงเป้าหมาย สนับสนุนการแก้ไขปัญหาสำหรับผู้เรียนที่ประสบปัญหา และมอบโอกาสในการเสริมสร้างความรู้สำหรับนักเรียนที่มีความสามารถสูง เพื่อให้มั่นใจว่าผู้เรียนทุกคนพัฒนาความเชี่ยวชาญในแนวคิดเรขาคณิตของกรวยผ่านการฝึกฝนอย่างเป็นระบบและต่อเนื่องที่สอดคล้องกับมาตรฐานทางคณิตศาสตร์
