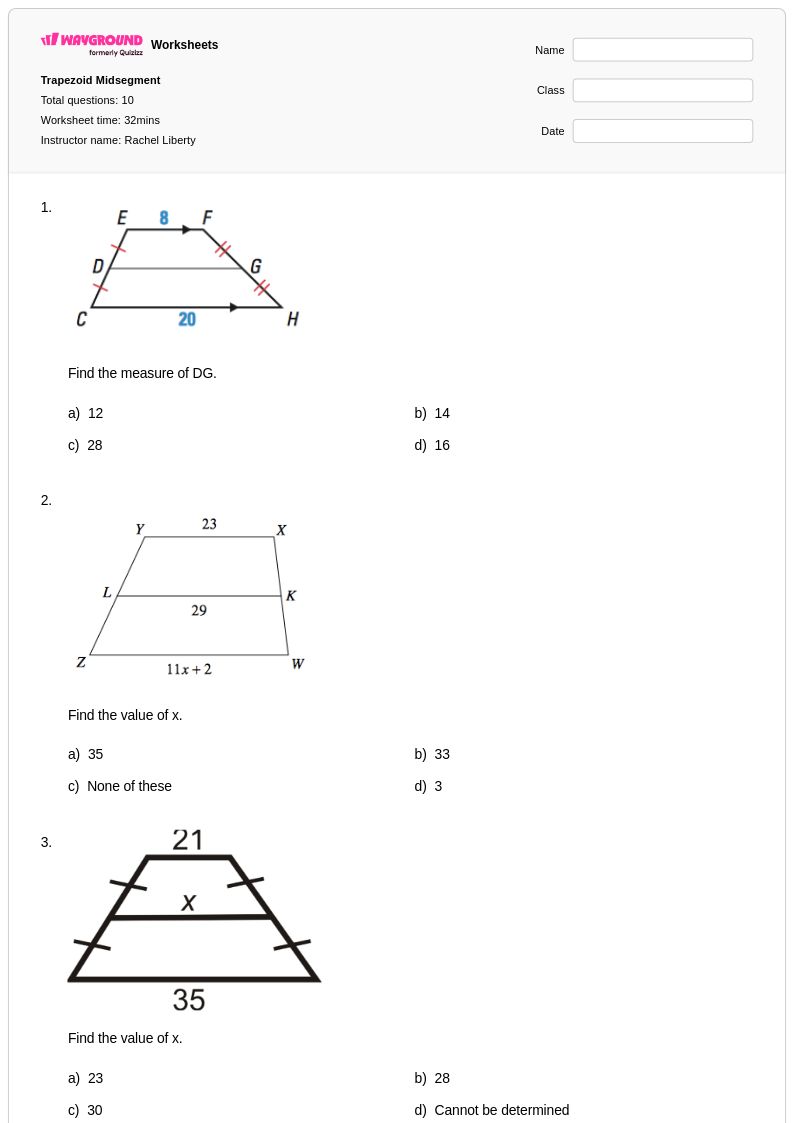
10Q
8th - 11th

33Q
8th - 10th

20Q
5th - Uni

20Q
5th - Uni

20Q
7th - 9th

35Q
8th - 10th
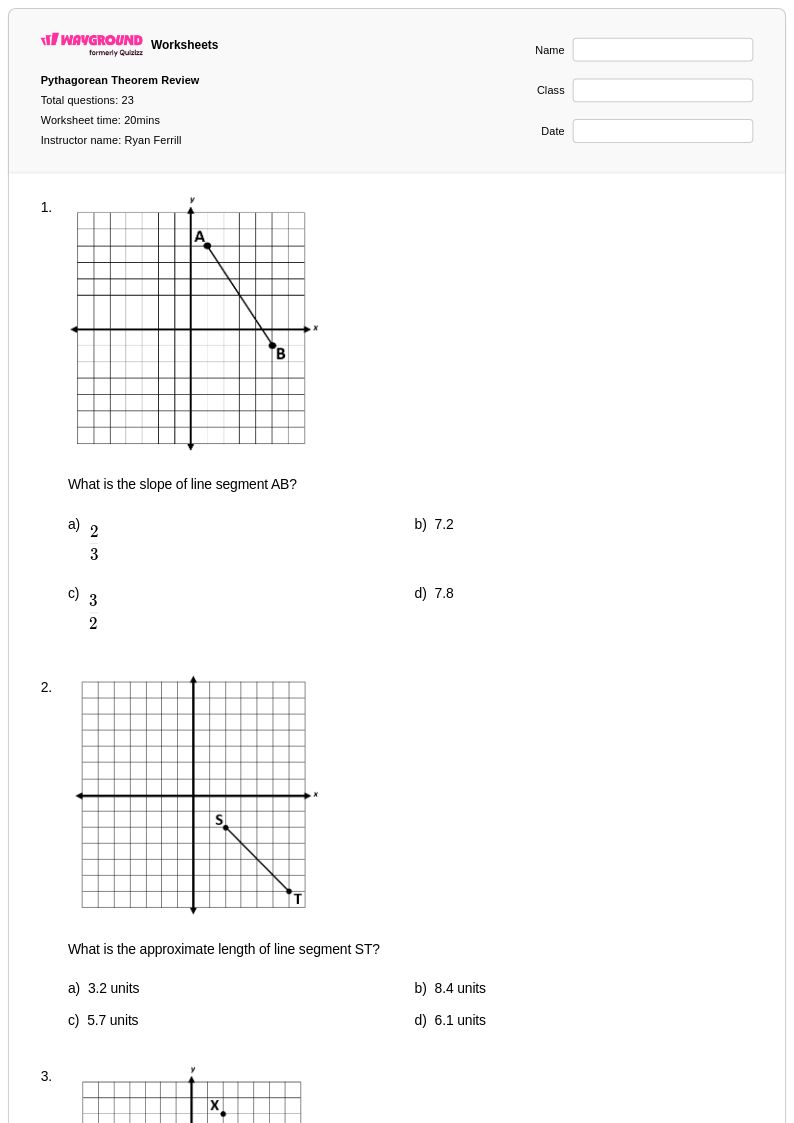
23Q
8th
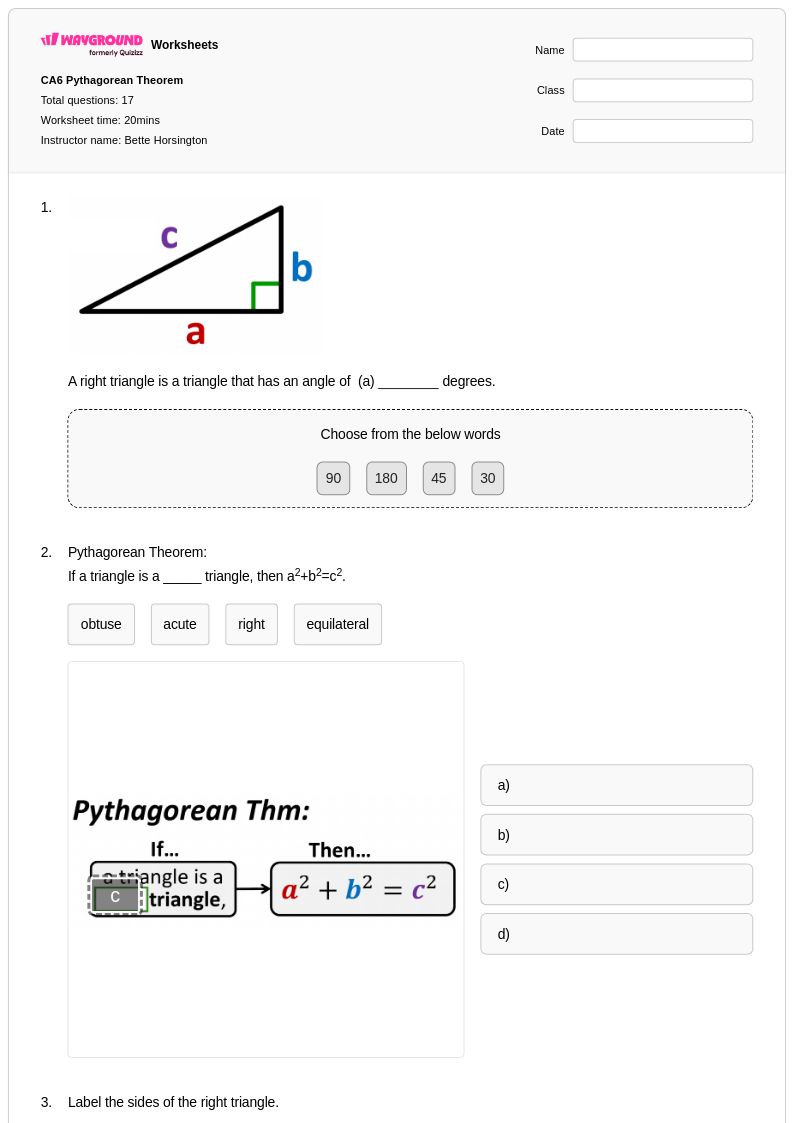
17Q
8th - Uni

40Q
8th

21Q
8th

12Q
8th
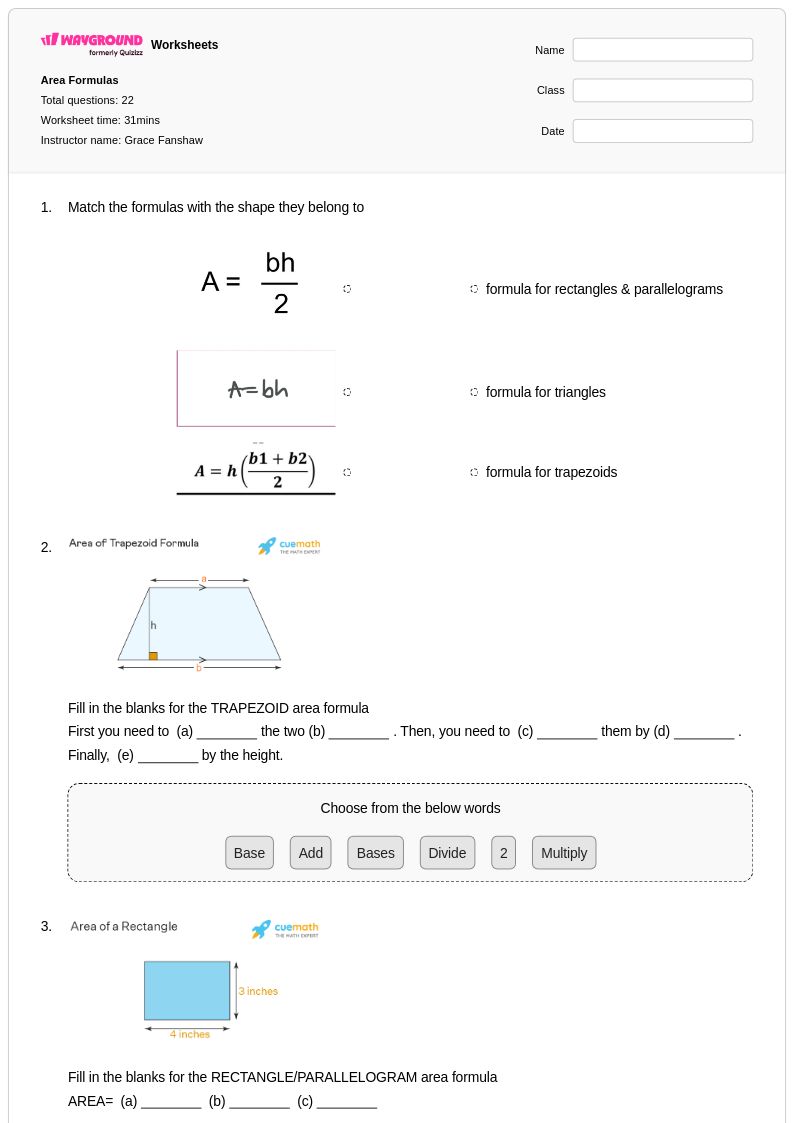
22Q
6th - 8th

8Q
6th - Uni
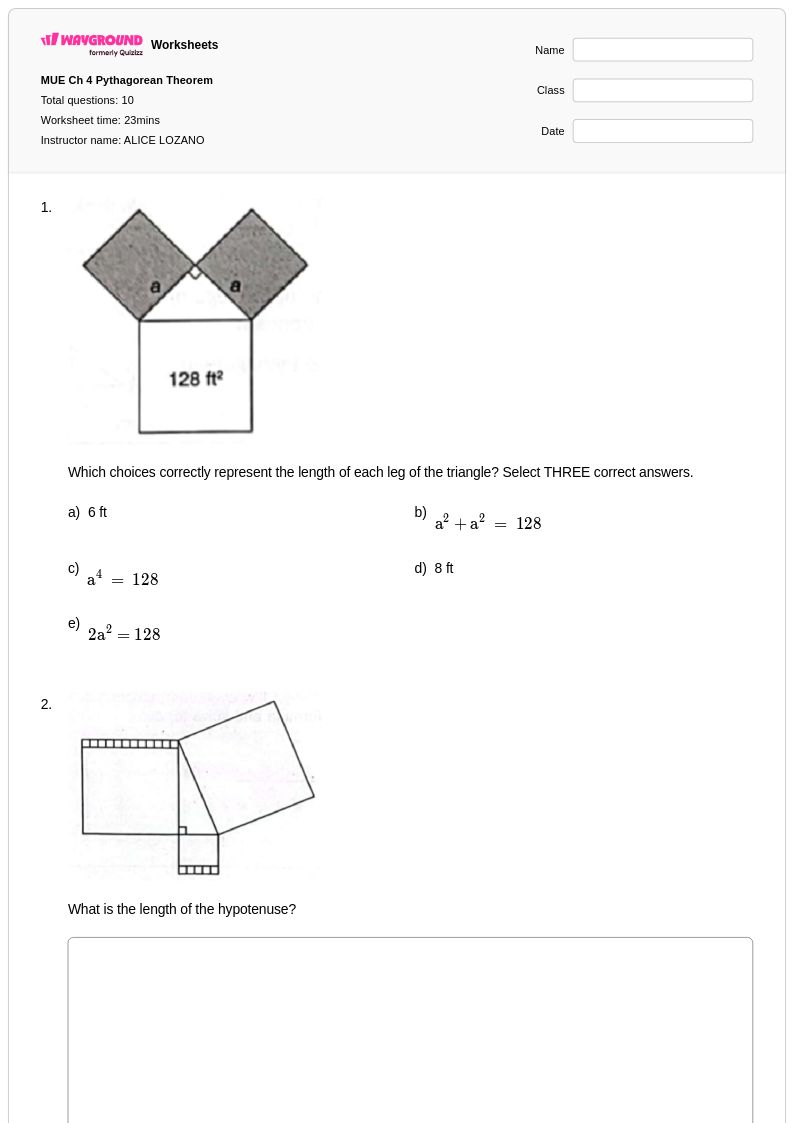
10Q
8th
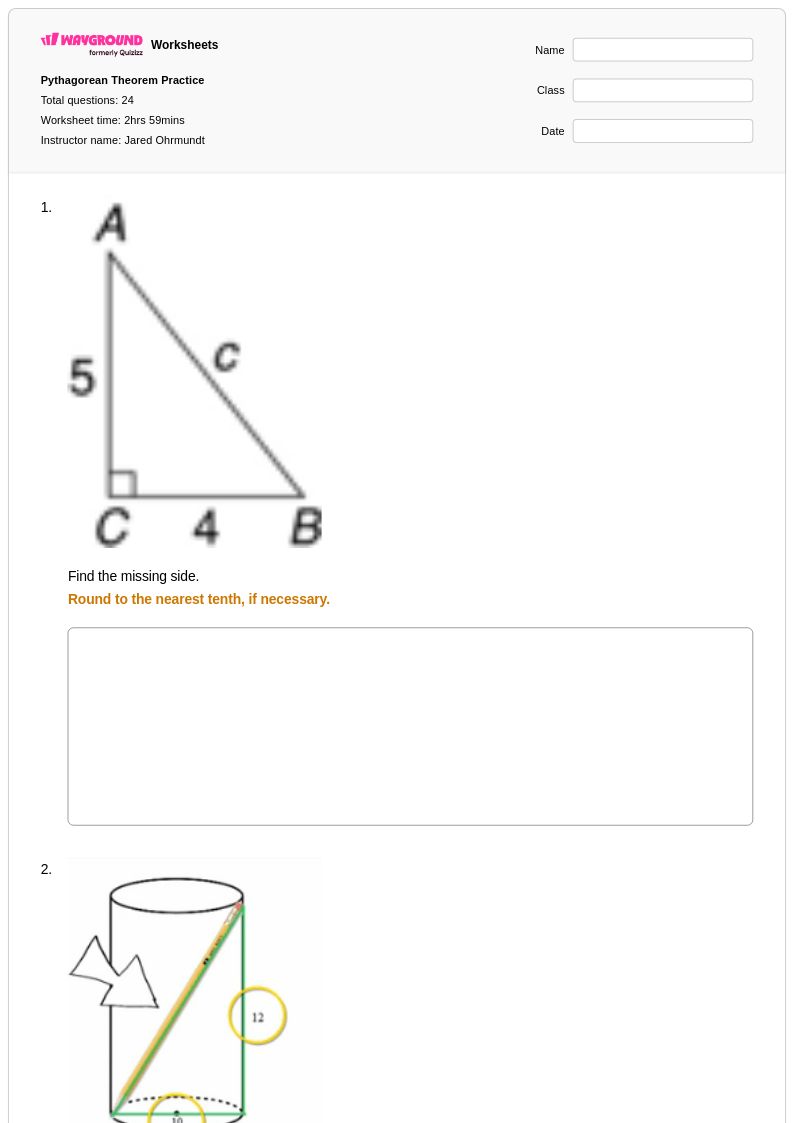
24Q
8th

11Q
8th

10Q
8th
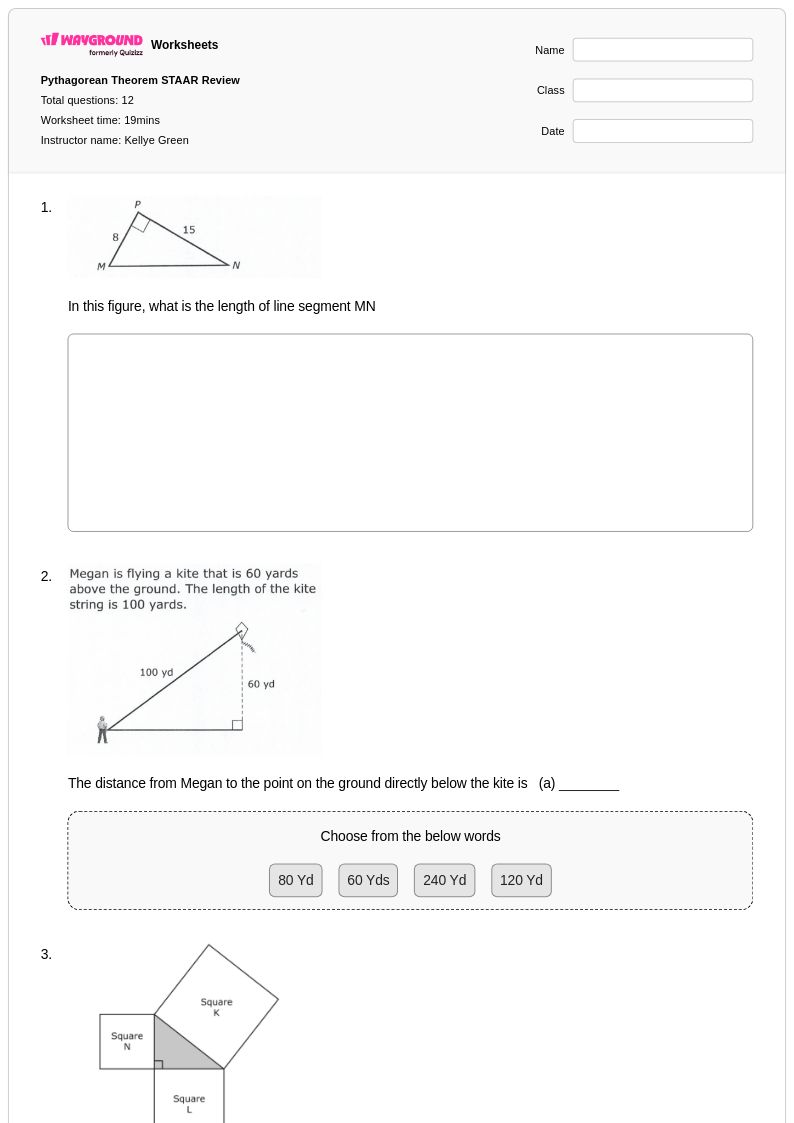
12Q
8th
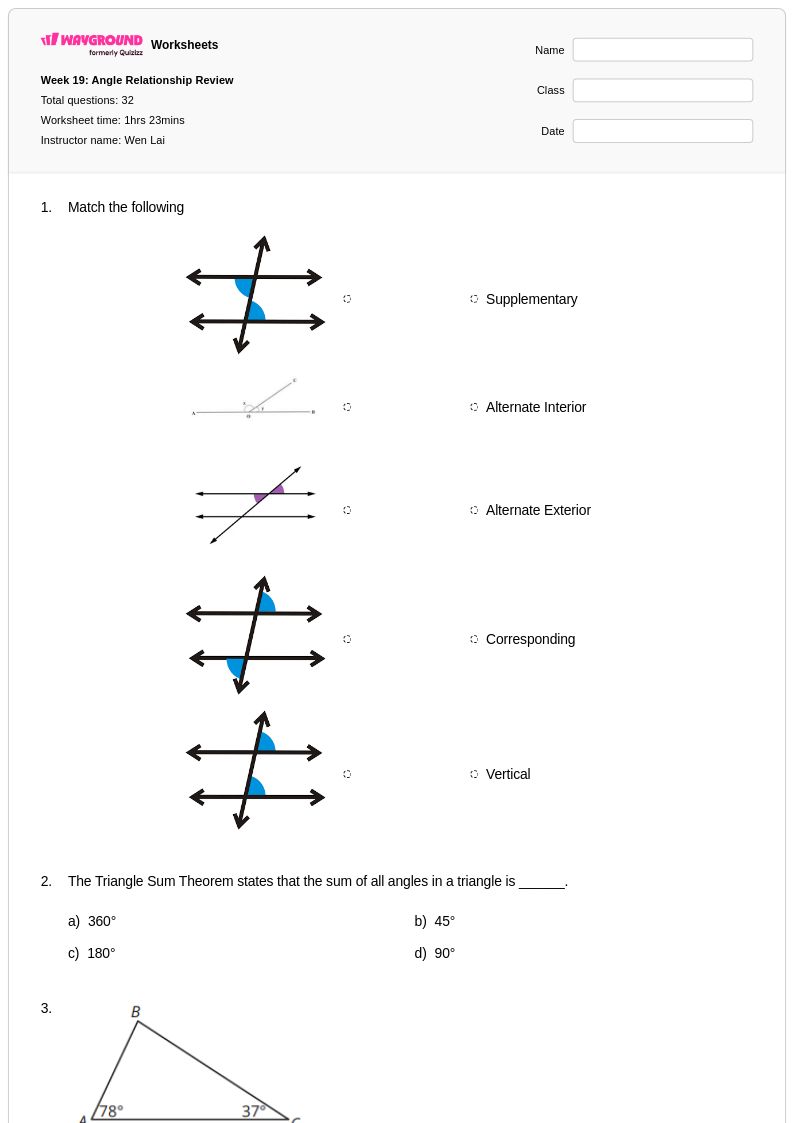
32Q
8th
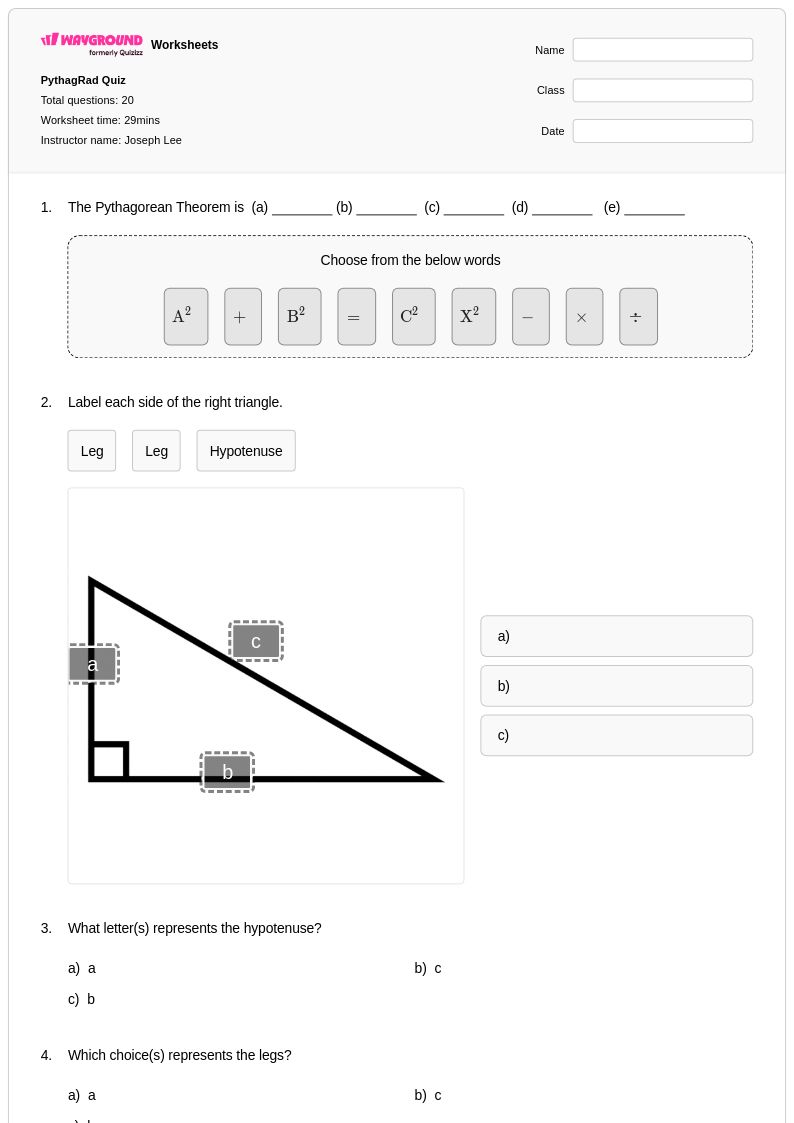
20Q
8th
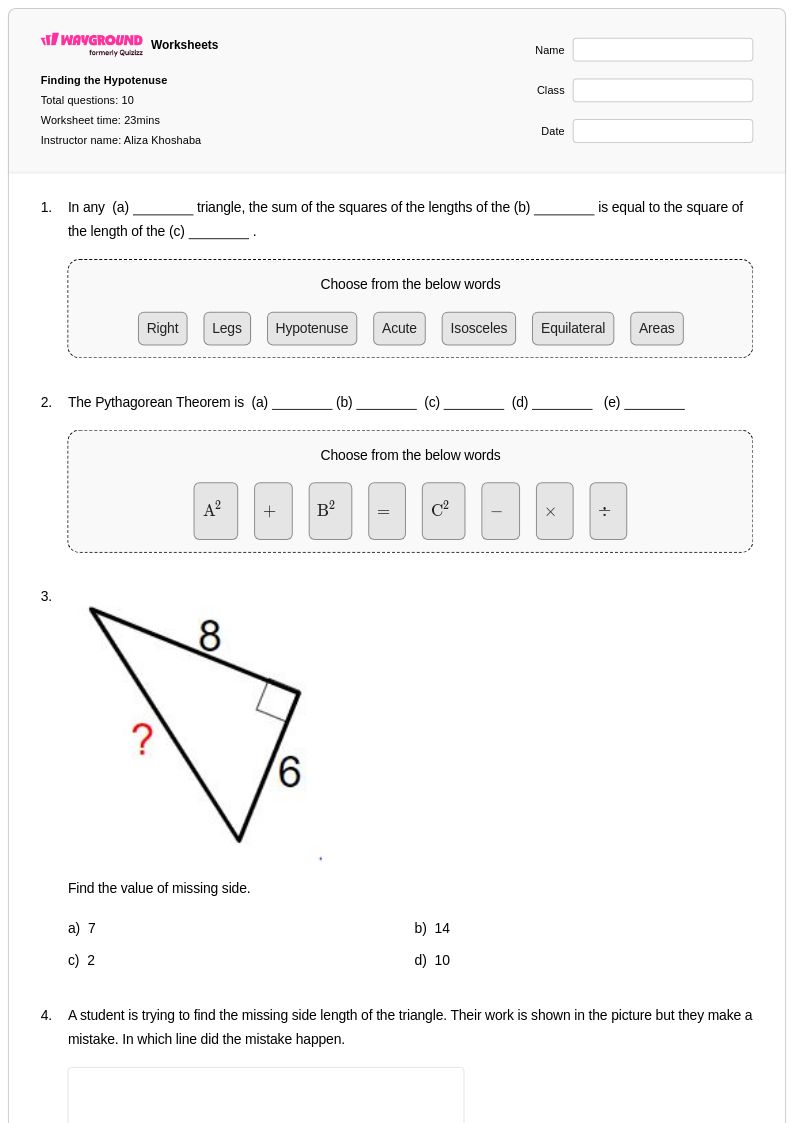
10Q
8th

15Q
8th
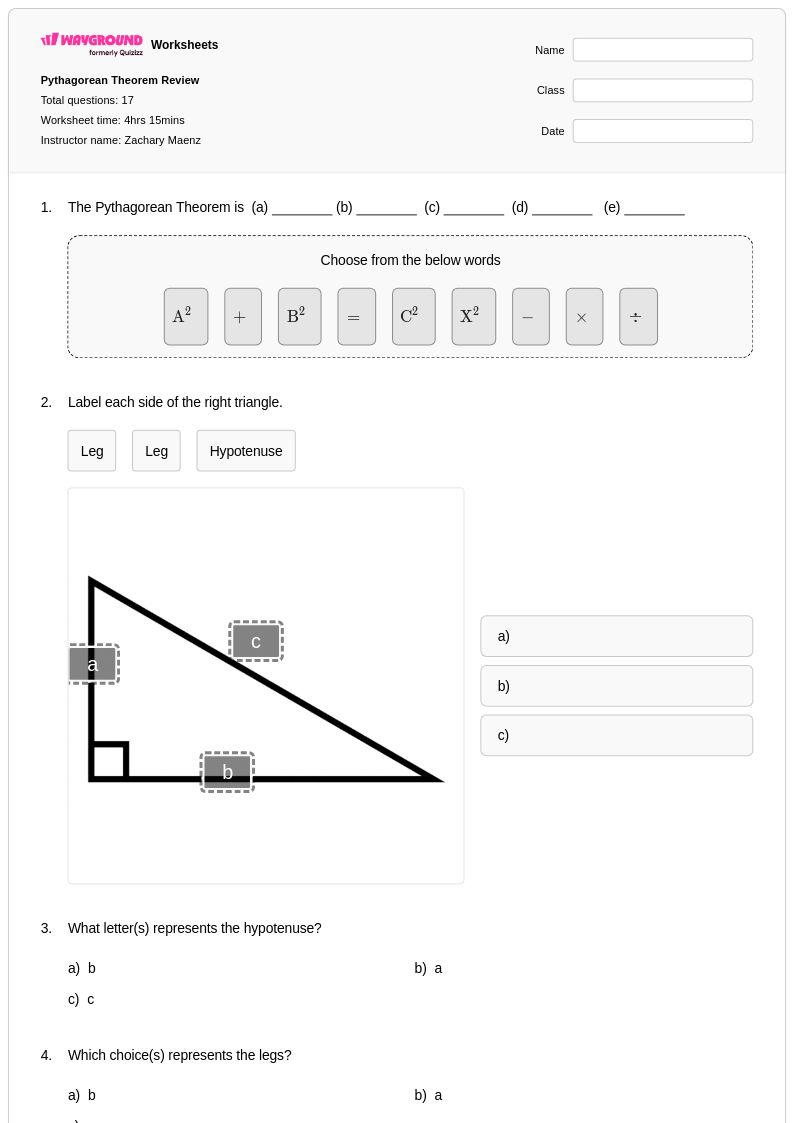
17Q
8th

201Q
8th
Explore otras hojas de trabajo de materias para ระดับ 8
สำรวจแผ่นงาน ทฤษฎีบทส่วนกลางรูปสี่เหลี่ยมคางหมู ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 8
ทฤษฎีบทส่วนกลางของรูปสี่เหลี่ยมคางหมูเป็นแนวคิดพื้นฐานในเรขาคณิตระดับชั้นมัธยมศึกษาปีที่ 2 และ Wayground (เดิมชื่อ Quizizz) ได้จัดทำแบบฝึกหัดที่ครอบคลุมซึ่งช่วยให้นักเรียนเข้าใจหลักการทางเรขาคณิตที่สำคัญนี้อย่างถ่องแท้ แหล่งข้อมูลทางการศึกษาเหล่านี้มุ่งเน้นไปที่การพัฒนาความเข้าใจของนักเรียนเกี่ยวกับความสัมพันธ์ระหว่างส่วนกลางของรูปสี่เหลี่ยมคางหมูกับฐานคู่ขนาน โดยเฉพาะอย่างยิ่ง ส่วนกลางจะขนานกับฐานทั้งสองและมีความยาวเท่ากับค่าเฉลี่ยของความยาวฐานทั้งสอง แบบฝึกหัดประกอบด้วยโจทย์ฝึกหัดที่หลากหลายซึ่งจะช่วยแนะนำนักเรียนในการระบุส่วนกลาง การคำนวณความยาว และการประยุกต์ใช้ทฤษฎีบทเพื่อแก้ปัญหาทางเรขาคณิตที่ซับซ้อน แบบฝึกหัดแต่ละชุดมาพร้อมกับเฉลยคำตอบโดยละเอียดซึ่งสนับสนุนทั้งการเรียนรู้ด้วยตนเองและการเรียนการสอนในห้องเรียน และครูสามารถเข้าถึงสื่อเหล่านี้ได้ในรูปแบบเอกสารพิมพ์ฟรีหรือไฟล์ PDF ที่ดาวน์โหลดได้ซึ่งสามารถบูรณาการเข้ากับแผนการสอนที่มีอยู่ได้อย่างราบรื่น
Wayground (เดิมชื่อ Quizizz) ช่วยเสริมศักยภาพครูผู้สอนด้วยแหล่งข้อมูลนับล้านที่สร้างโดยครูผู้สอนโดยเฉพาะ ซึ่งออกแบบมาสำหรับการสอนทฤษฎีบทส่วนกลางของรูปสี่เหลี่ยมคางหมูโดยเฉพาะ มีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพ ช่วยให้ครูสามารถค้นหาสื่อที่สอดคล้องกับมาตรฐานหลักสูตรและความต้องการของนักเรียนได้อย่างรวดเร็ว เครื่องมือการปรับระดับความยากง่ายของแพลตฟอร์มช่วยให้ครูสามารถปรับแต่งแบบฝึกหัดสำหรับระดับการเรียนรู้ต่างๆ เพื่อให้มั่นใจว่าทั้งนักเรียนที่เรียนรู้ช้าและนักเรียนที่เรียนรู้เร็วสามารถมีส่วนร่วมกับเนื้อหาได้อย่างมีความหมายผ่านระดับความท้าทายที่เหมาะสมและการสนับสนุนแบบค่อยเป็นค่อยไป แหล่งข้อมูลเหล่านี้มีให้เลือกทั้งแบบพิมพ์ได้และแบบดิจิทัล รวมถึงการดาวน์โหลดไฟล์ PDF ที่สะดวก ทำให้สามารถนำไปใช้ได้หลากหลายในการสอนในชั้นเรียน การบ้าน การเรียนเสริม และกิจกรรมเสริม ครูสามารถวางแผนหน่วยการเรียนรู้เรขาคณิตที่ครอบคลุมได้อย่างมีประสิทธิภาพ ในขณะเดียวกันก็มีความยืดหยุ่นในการปรับเปลี่ยนสื่อสำหรับการฝึกฝนทักษะเฉพาะด้าน การประเมินผลระหว่างเรียน และเส้นทางการเรียนรู้เฉพาะบุคคลที่สนับสนุนการเติบโตทางคณิตศาสตร์ของนักเรียนทุกคน
