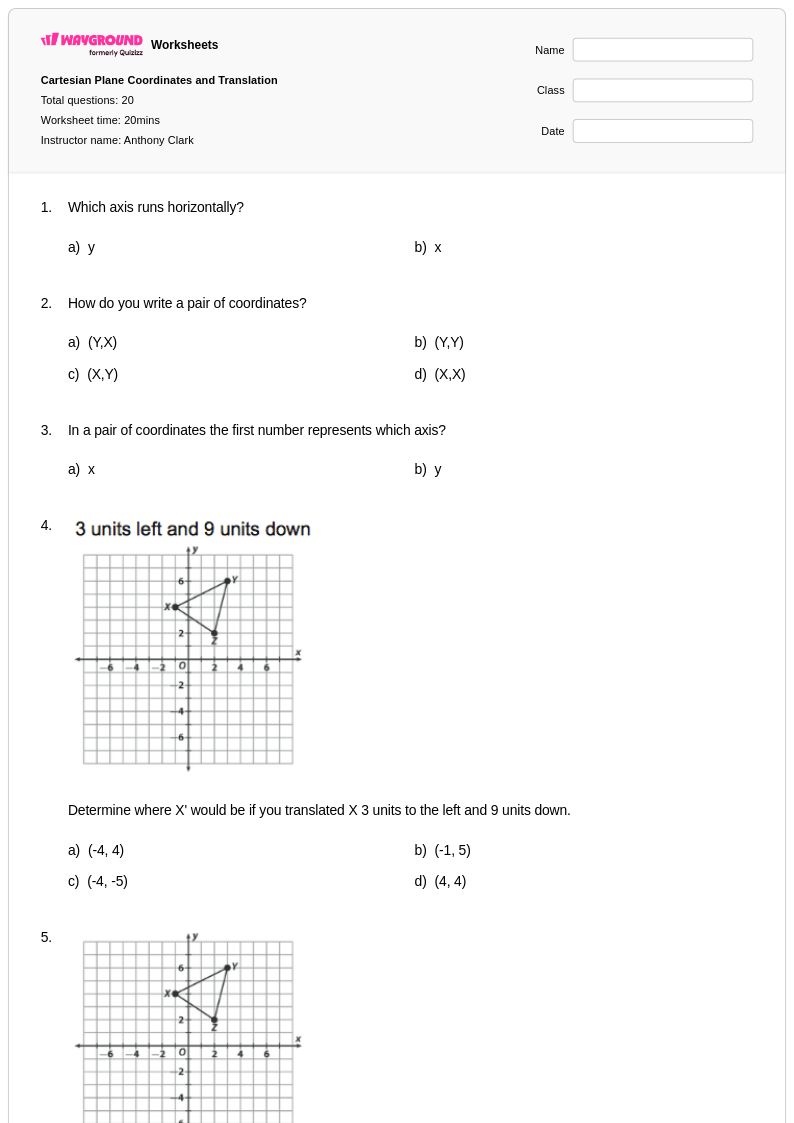
20 Hỏi
8th - Uni
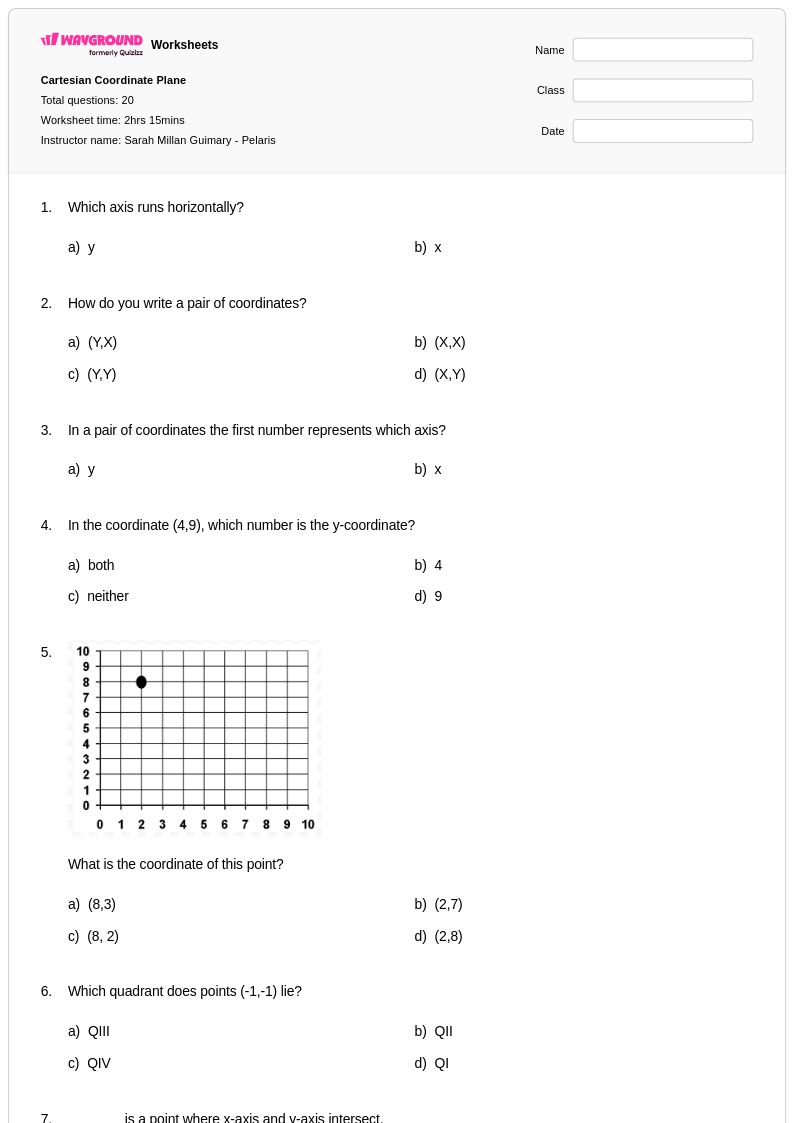
20 Hỏi
8th

10 Hỏi
8th
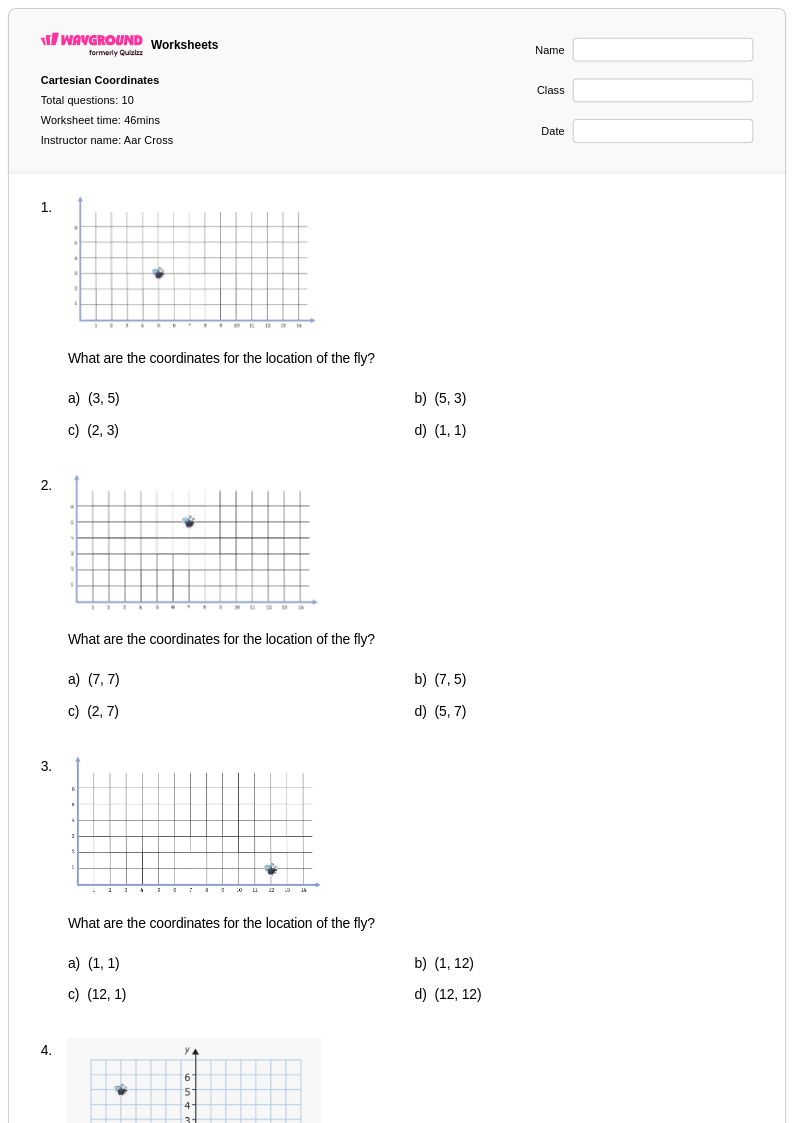
10 Hỏi
8th

15 Hỏi
8th
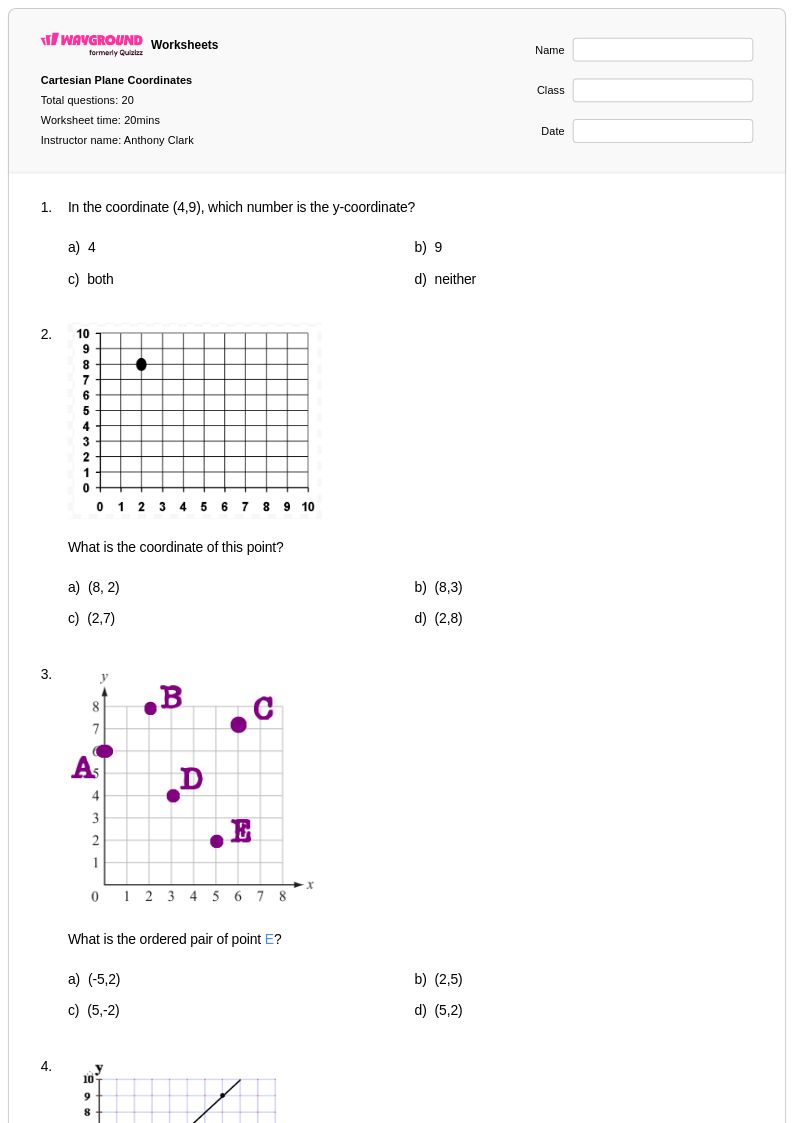
20 Hỏi
7th - Uni
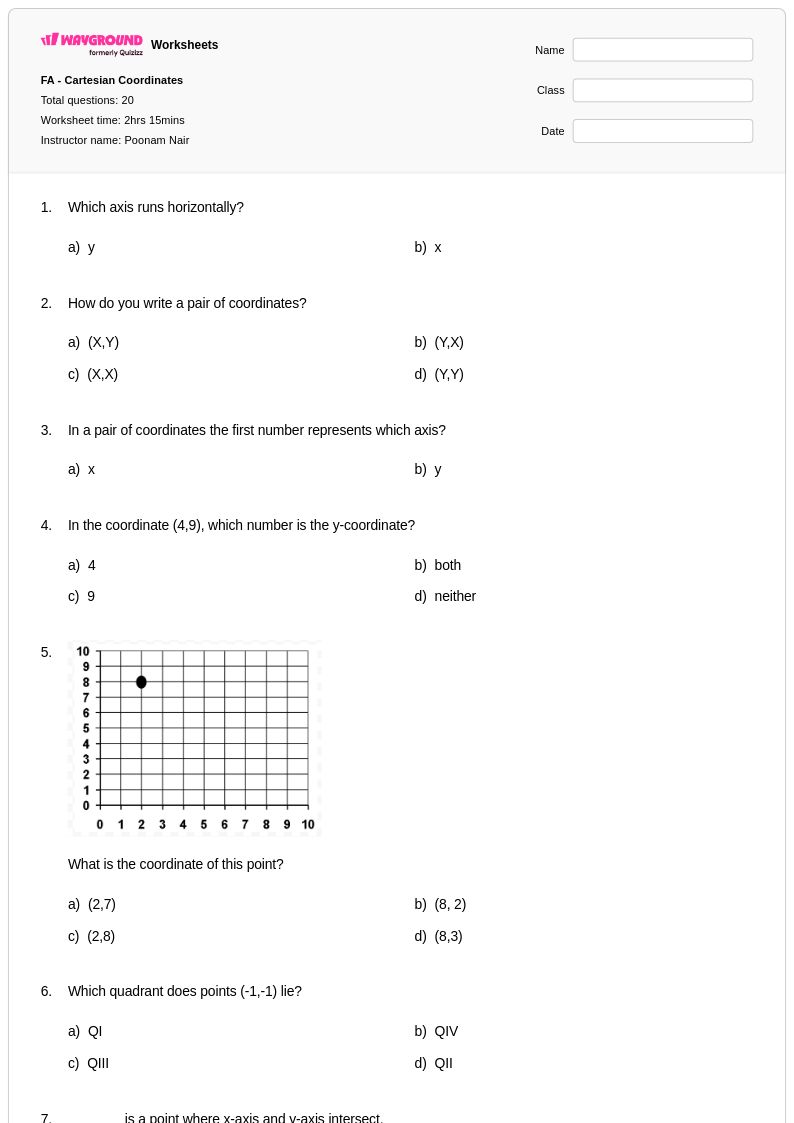
20 Hỏi
5th - Uni

40 Hỏi
8th
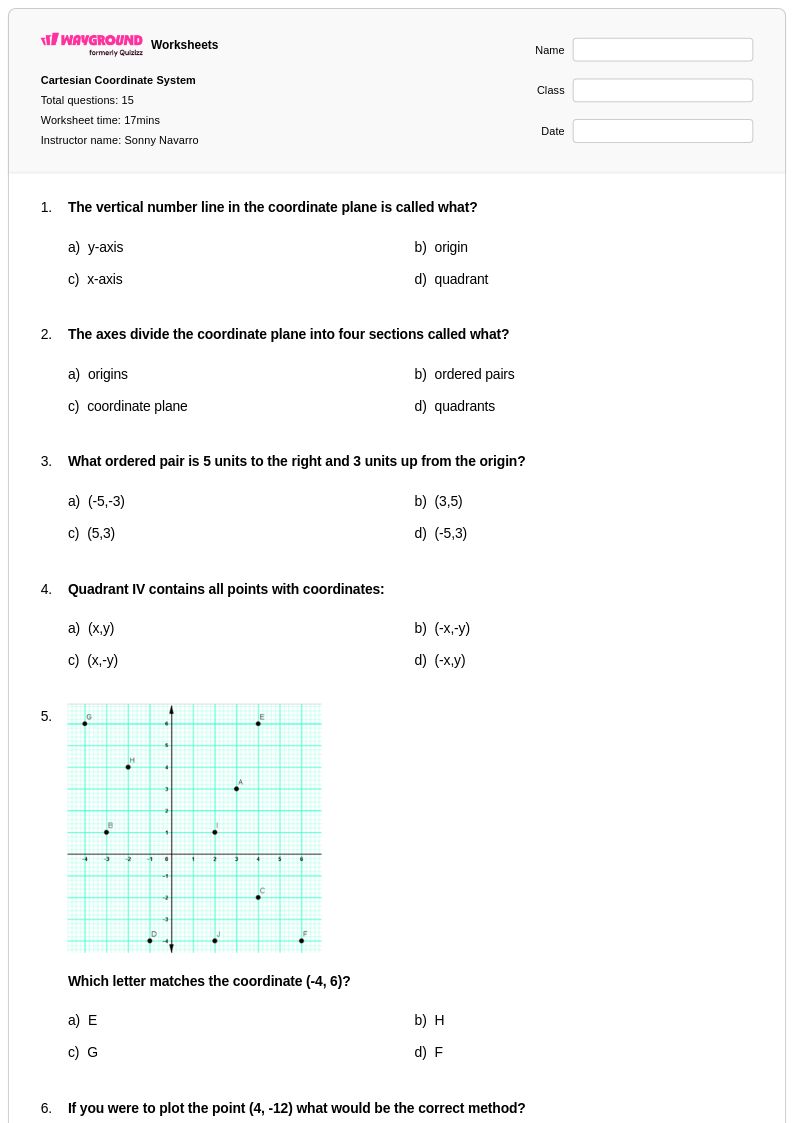
15 Hỏi
8th

10 Hỏi
8th

10 Hỏi
7th - Uni
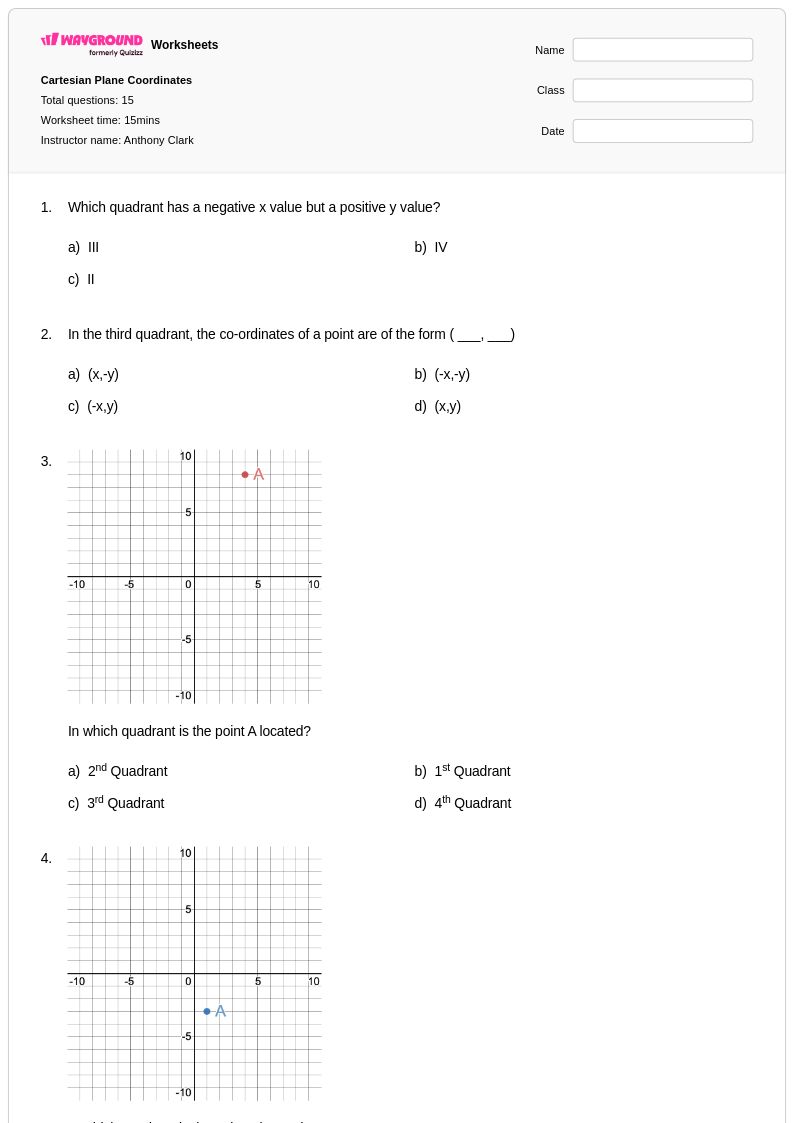
15 Hỏi
7th - Uni
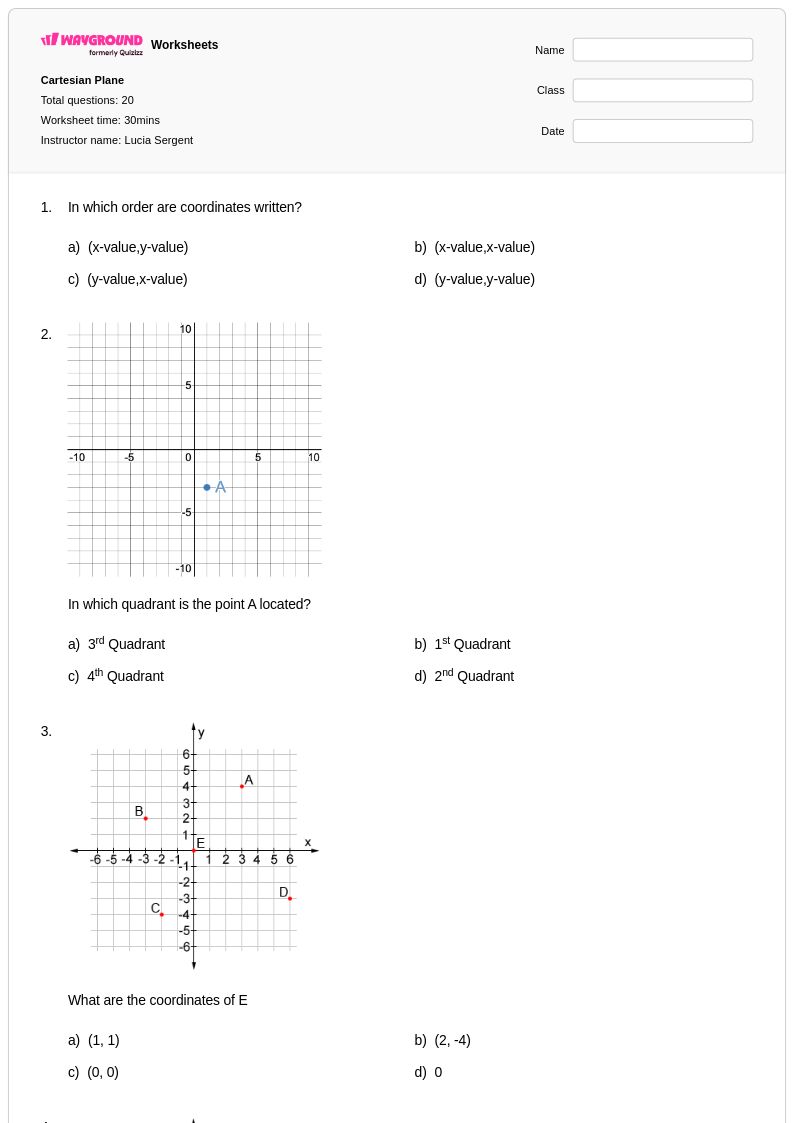
20 Hỏi
8th
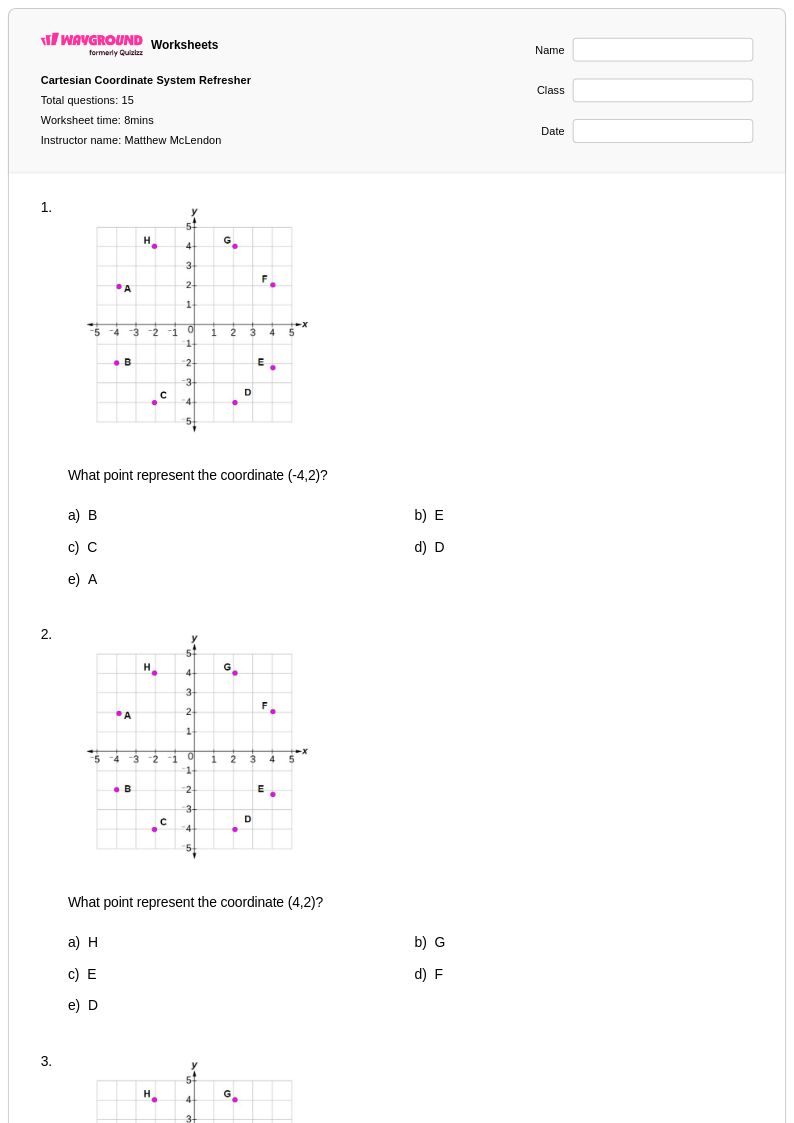
15 Hỏi
8th

15 Hỏi
8th - Uni
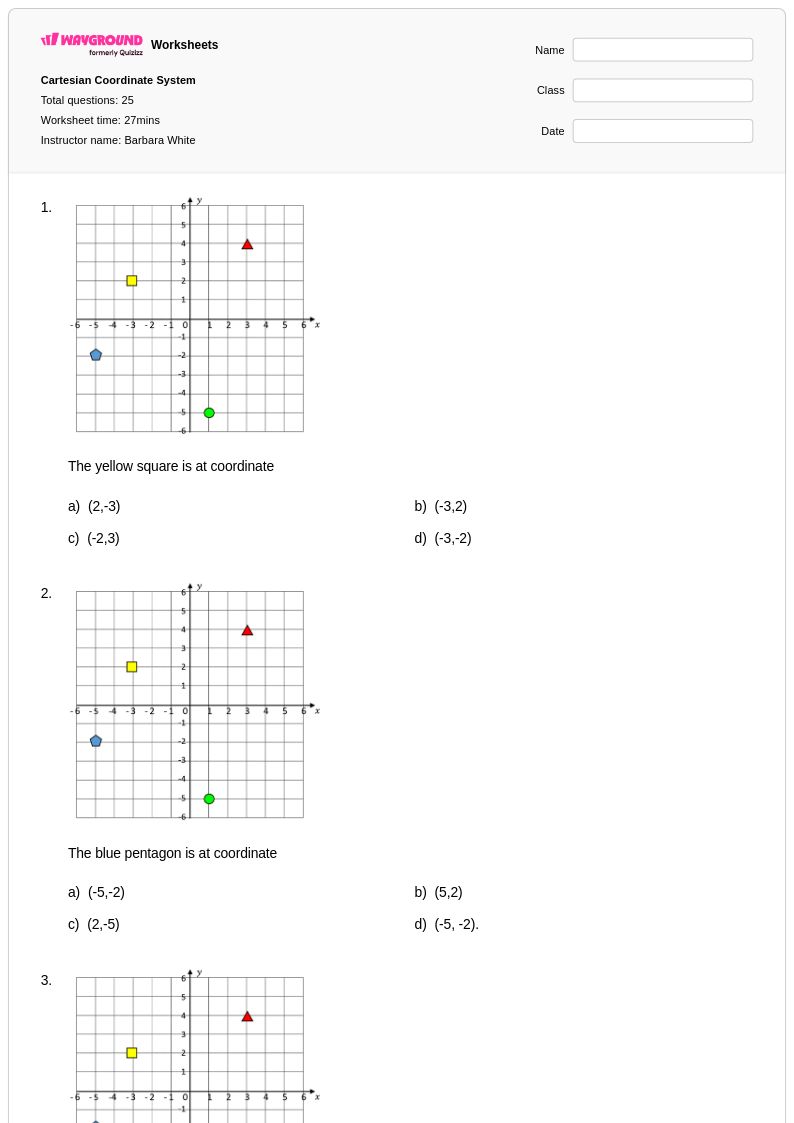
25 Hỏi
8th
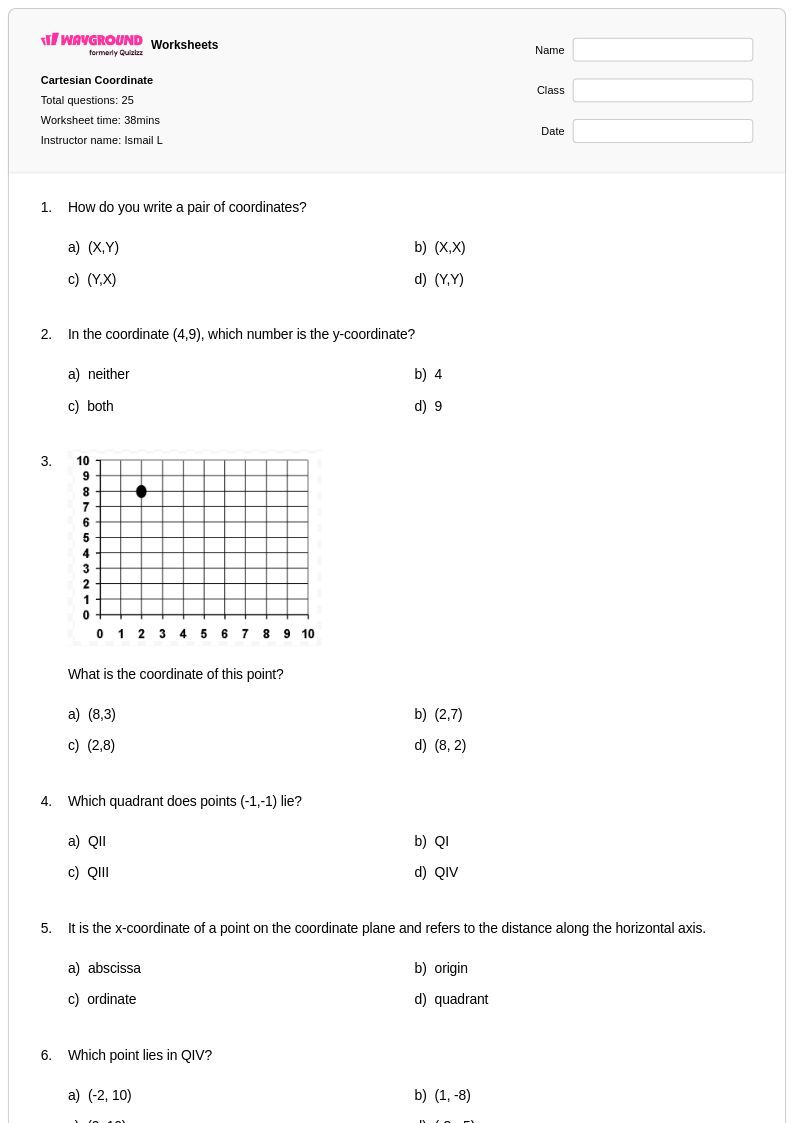
25 Hỏi
8th
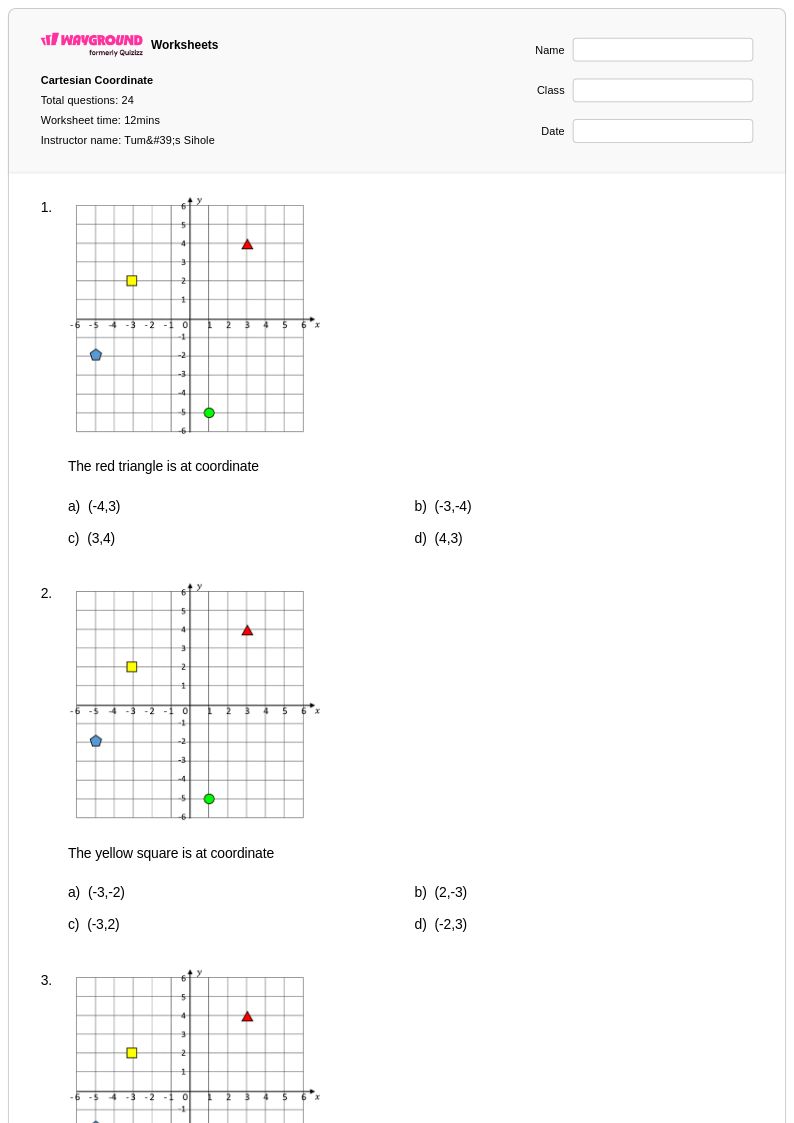
24 Hỏi
8th

11 Hỏi
8th
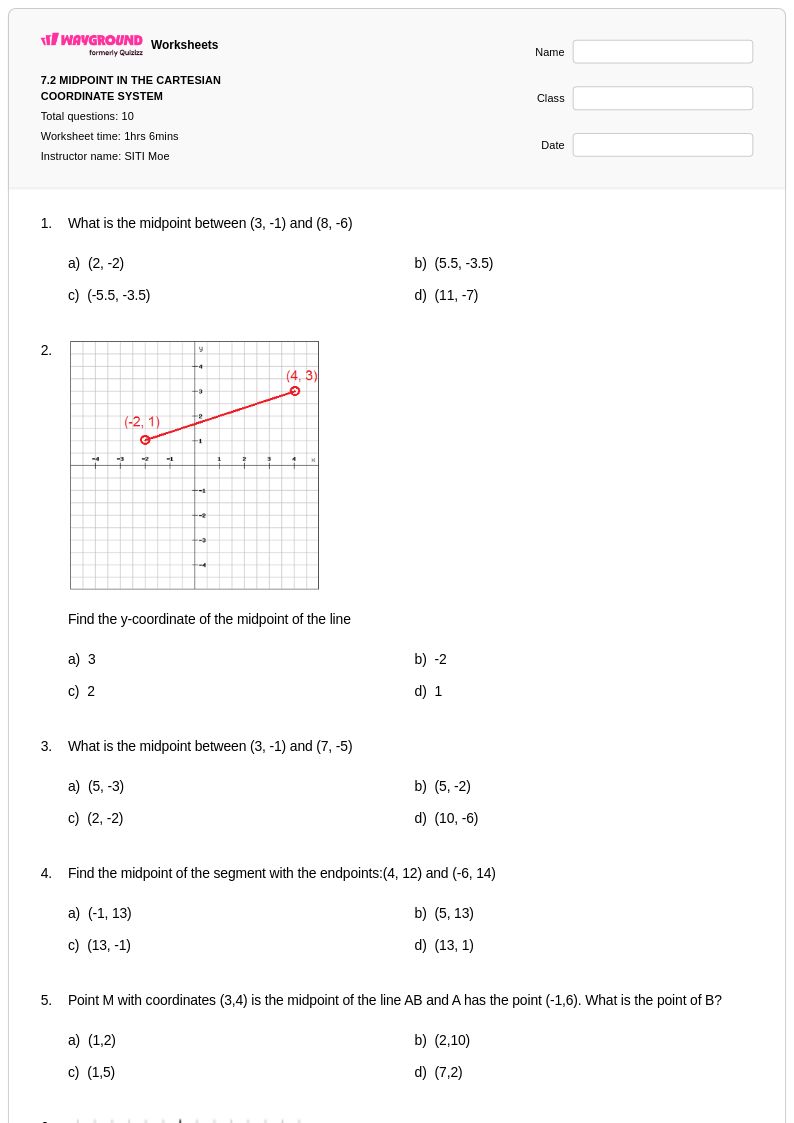
10 Hỏi
8th
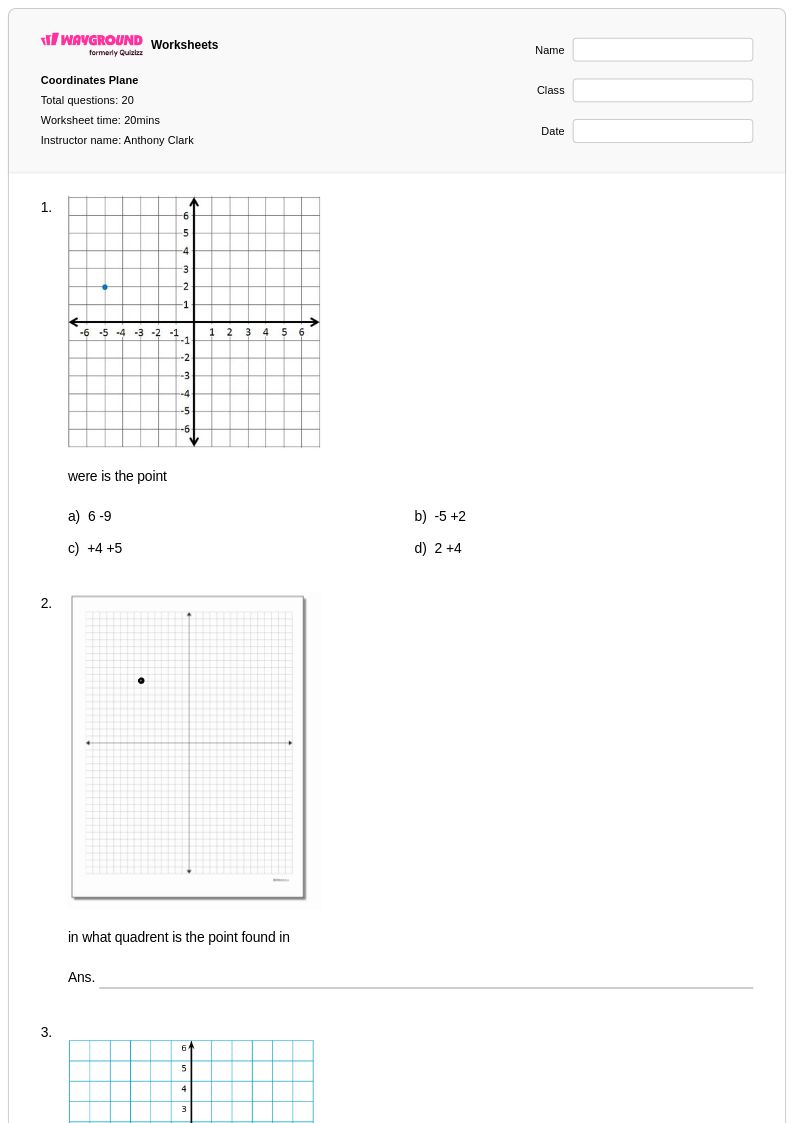
20 Hỏi
6th - Uni
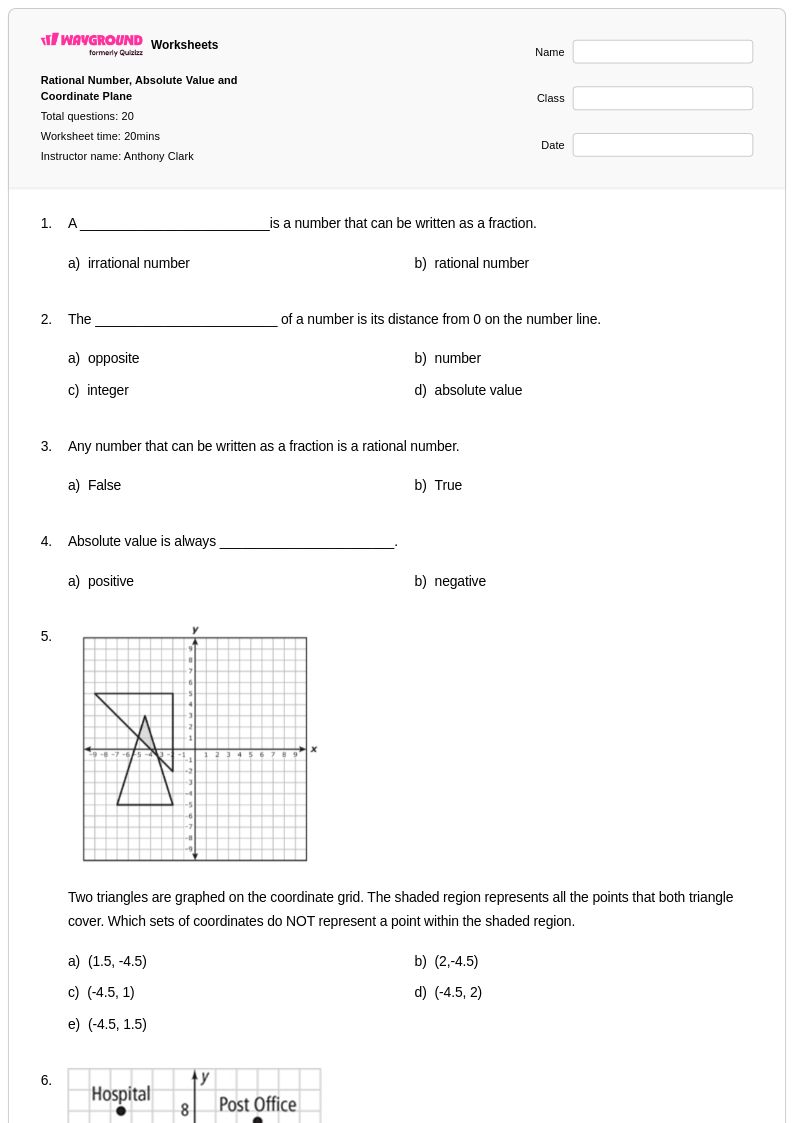
20 Hỏi
6th - Uni
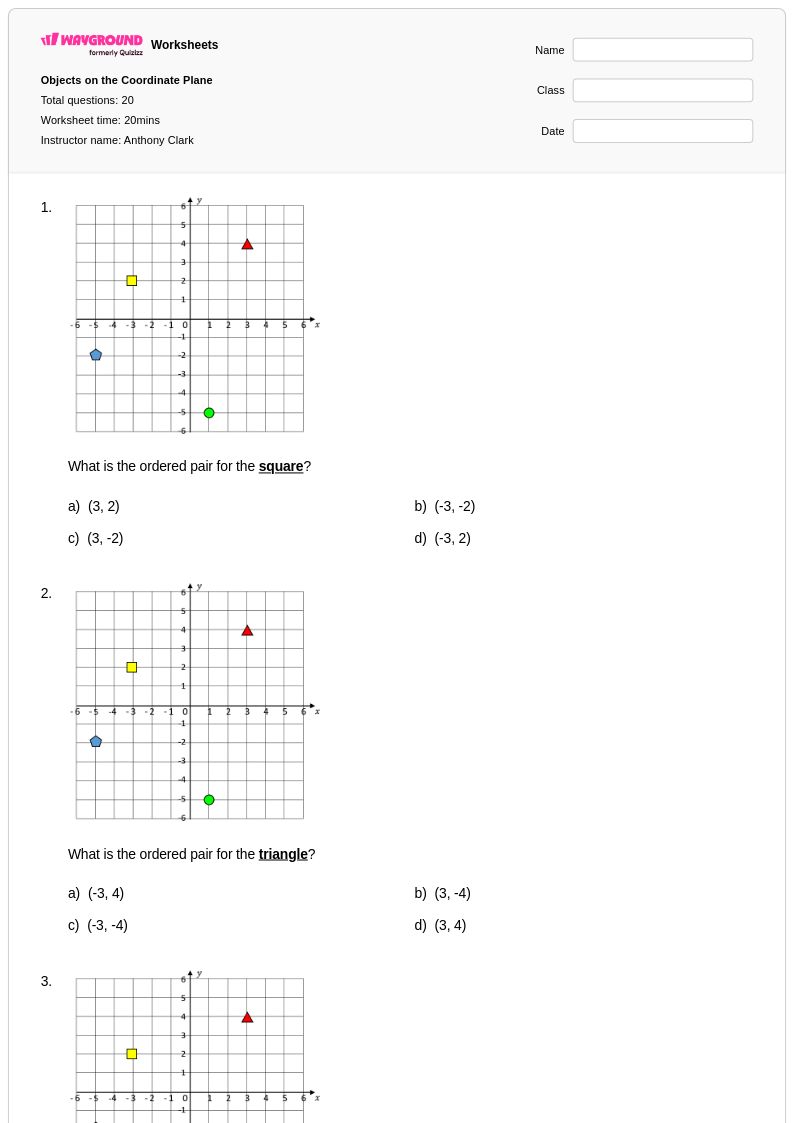
20 Hỏi
6th - Uni
Khám phá พิกัดคาร์ทีเซียน Bảng tính theo cấp độ
Khám phá các bảng tính chủ đề khác cho ระดับ 8
สำรวจแผ่นงาน พิกัดคาร์ทีเซียน ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 8
แบบฝึกหัดพิกัดคาร์ทีเซียนสำหรับนักเรียนชั้น ม.2 ที่มีให้ใช้งานผ่าน Wayground (เดิมคือ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมเกี่ยวกับการลงจุด การระบุควอดแรนต์ การคำนวณระยะทาง และการทำความเข้าใจความสัมพันธ์ระหว่างคู่ลำดับและการแสดงผลเชิงกราฟบนระนาบพิกัด แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยเสริมสร้างความสามารถในการคิดเชิงพื้นที่ของนักเรียน ในขณะเดียวกันก็สร้างทักษะพื้นฐานที่จำเป็นสำหรับแนวคิดพีชคณิตขั้นสูง รวมถึงสมการเชิงเส้น การแปลง และการพิสูจน์ทางเรขาคณิต แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดที่สนับสนุนทั้งการฝึกฝนด้วยตนเองและการสอนแบบมีผู้แนะนำ พร้อมเอกสารประกอบการเรียนฟรีที่ครอบคลุมทุกอย่างตั้งแต่การลงจุดพื้นฐานไปจนถึงปัญหาเรขาคณิตพิกัดที่ซับซ้อน ซึ่งท้าทายให้นักเรียนประยุกต์ใช้ทฤษฎีบทพีทาโกรัสและสูตรจุดกึ่งกลางภายในระบบสี่ควอดแรนต์
Wayground (เดิมคือ Quizizz) ช่วยให้ครูผู้สอนเข้าถึงแหล่งข้อมูลพิกัดคาร์ทีเซียนนับล้านรายการที่สร้างโดยครูผู้สอน ซึ่งสามารถค้นหา กรอง และปรับแต่งได้อย่างง่ายดายเพื่อให้ตรงกับวัตถุประสงค์การเรียนรู้เฉพาะและข้อกำหนดการจัดเรียงมาตรฐาน เครื่องมือปรับระดับความยากง่ายที่ทรงประสิทธิภาพของแพลตฟอร์มนี้ ช่วยให้ครูสามารถปรับเปลี่ยนแบบฝึกหัดระนาบพิกัดให้เหมาะสมกับระดับความสามารถต่างๆ ตั้งแต่ผู้เรียนที่เรียนรู้ช้าและต้องการความช่วยเหลือเพิ่มเติมเกี่ยวกับพิกัดบวก ไปจนถึงนักเรียนระดับสูงที่พร้อมสำหรับโจทย์ท้าทายที่เกี่ยวข้องกับการสะท้อน การหมุน และการคำนวณระยะทางในทั้งสี่ควอดแรนต์ สื่อการเรียนการสอนอเนกประสงค์เหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่พิมพ์ได้ และเวอร์ชันดิจิทัลแบบโต้ตอบ ช่วยสนับสนุนการวางแผนบทเรียนที่มีประสิทธิภาพ พร้อมทั้งให้ครูมีตัวเลือกที่ยืดหยุ่นสำหรับการแก้ไขปัญหา การฝึกฝนทักษะ และกิจกรรมเสริมความรู้ ซึ่งสามารถบูรณาการเข้ากับหลักสูตรเรขาคณิตระดับชั้น ม.2 ได้อย่างราบรื่น
