
10Q
8th
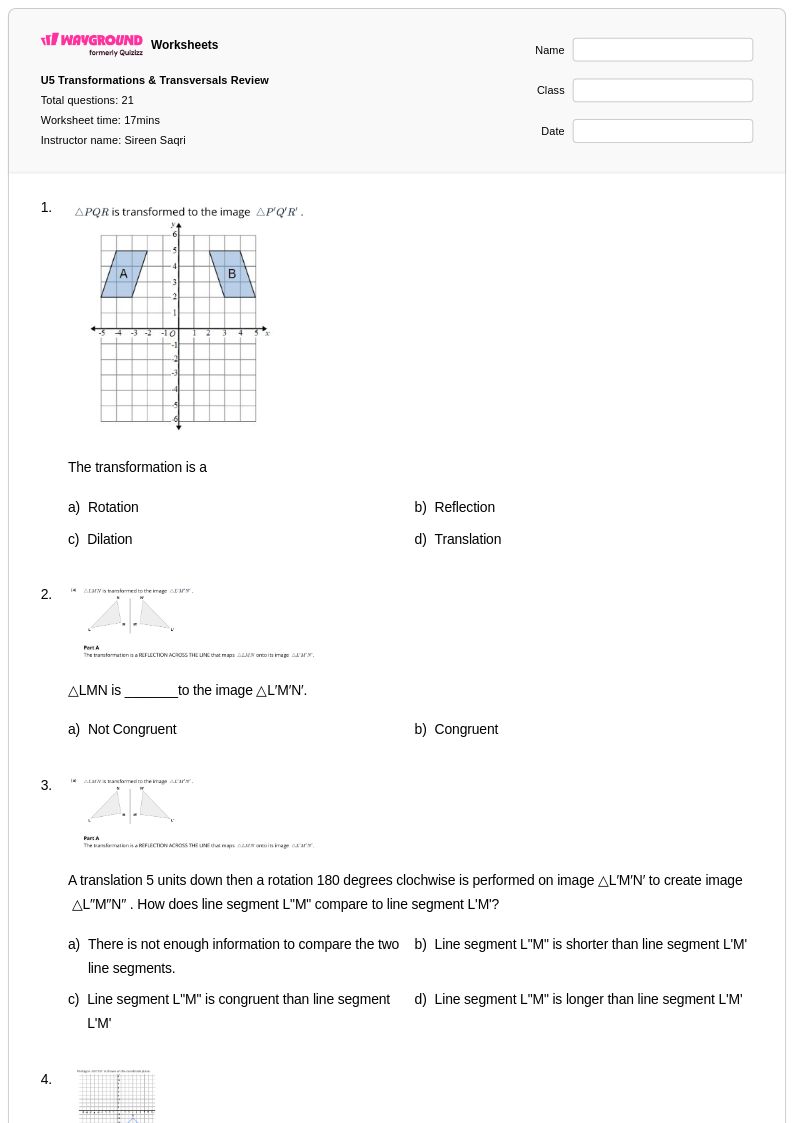
21Q
8th

86Q
8th
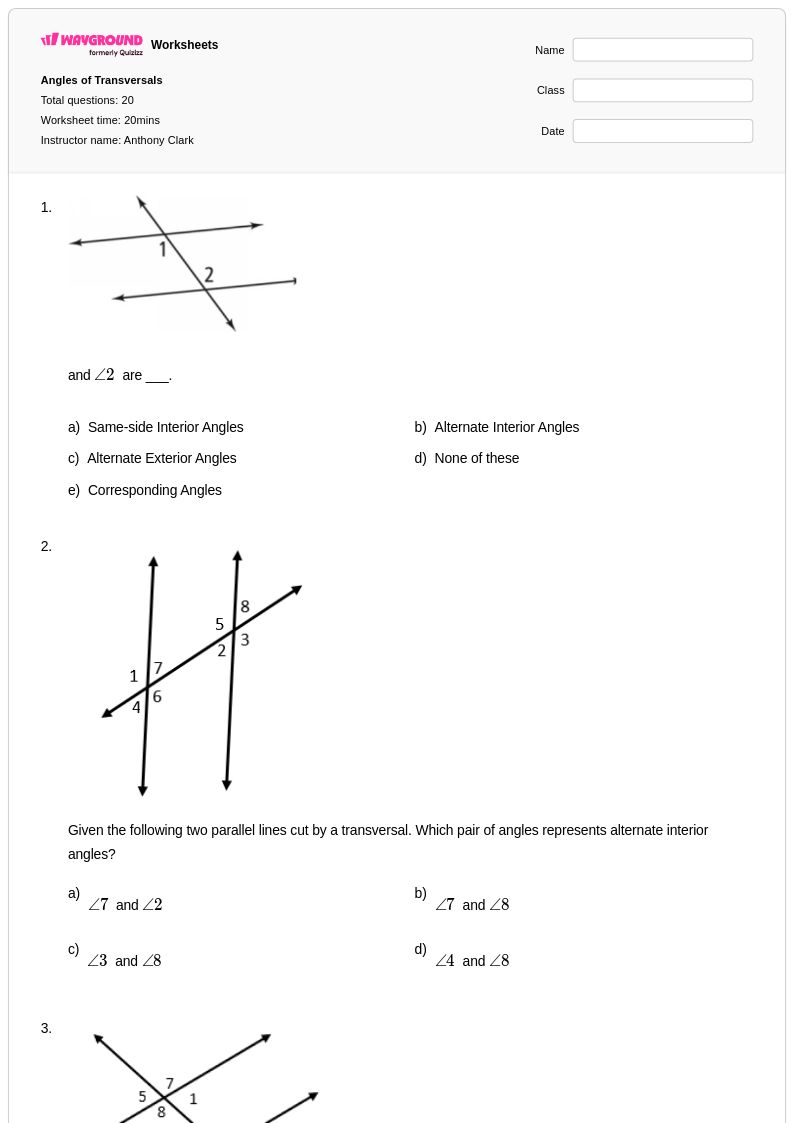
20Q
8th - Uni

20Q
8th - Uni
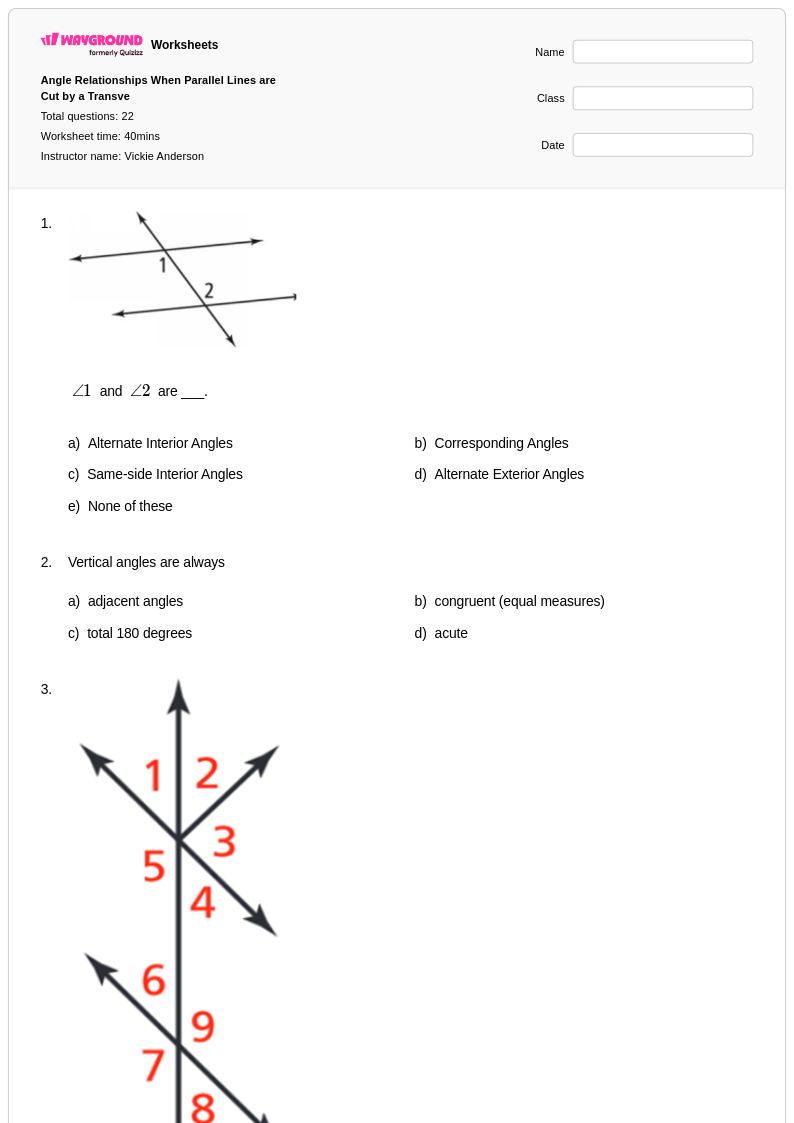
22Q
8th
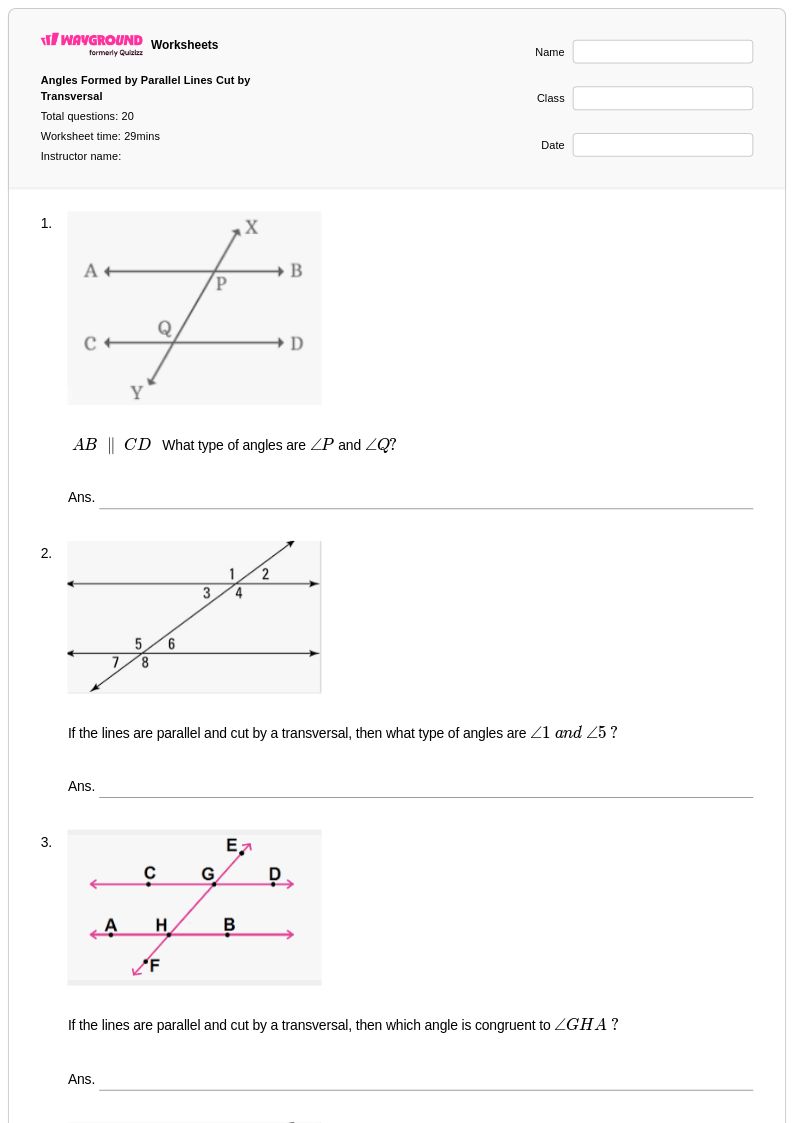
20Q
8th - 11th

25Q
8th
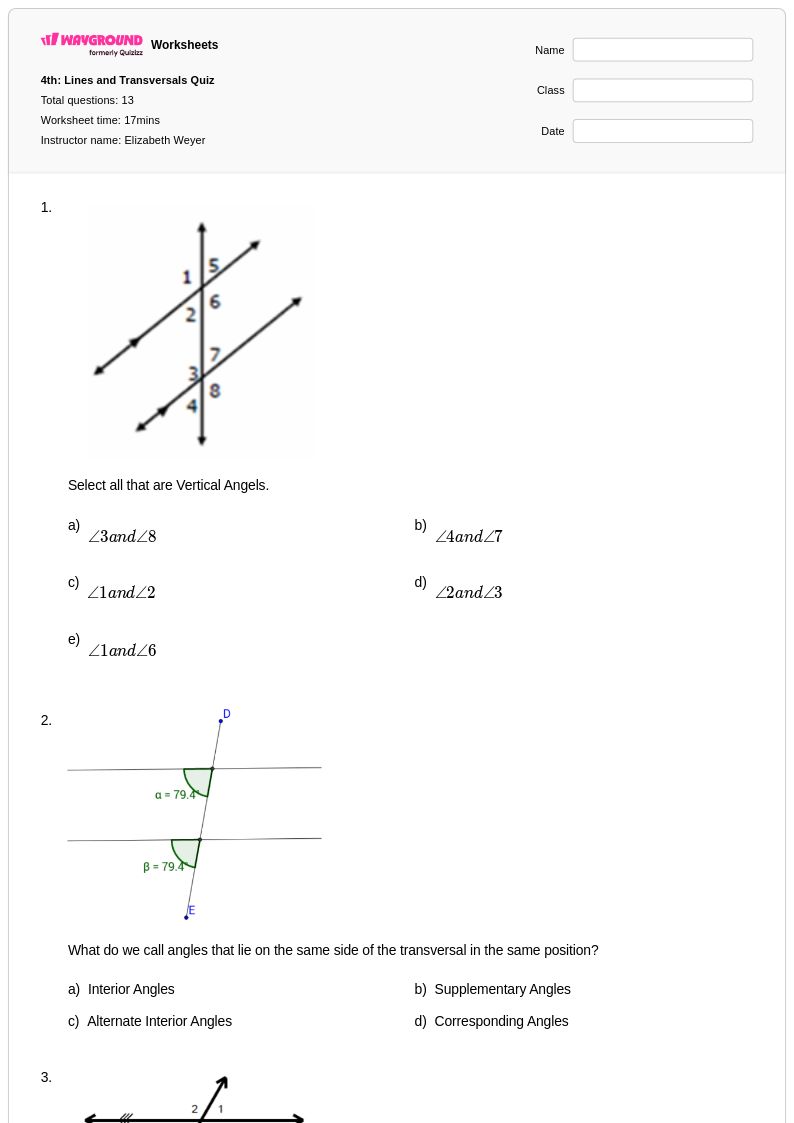
13Q
8th - 11th
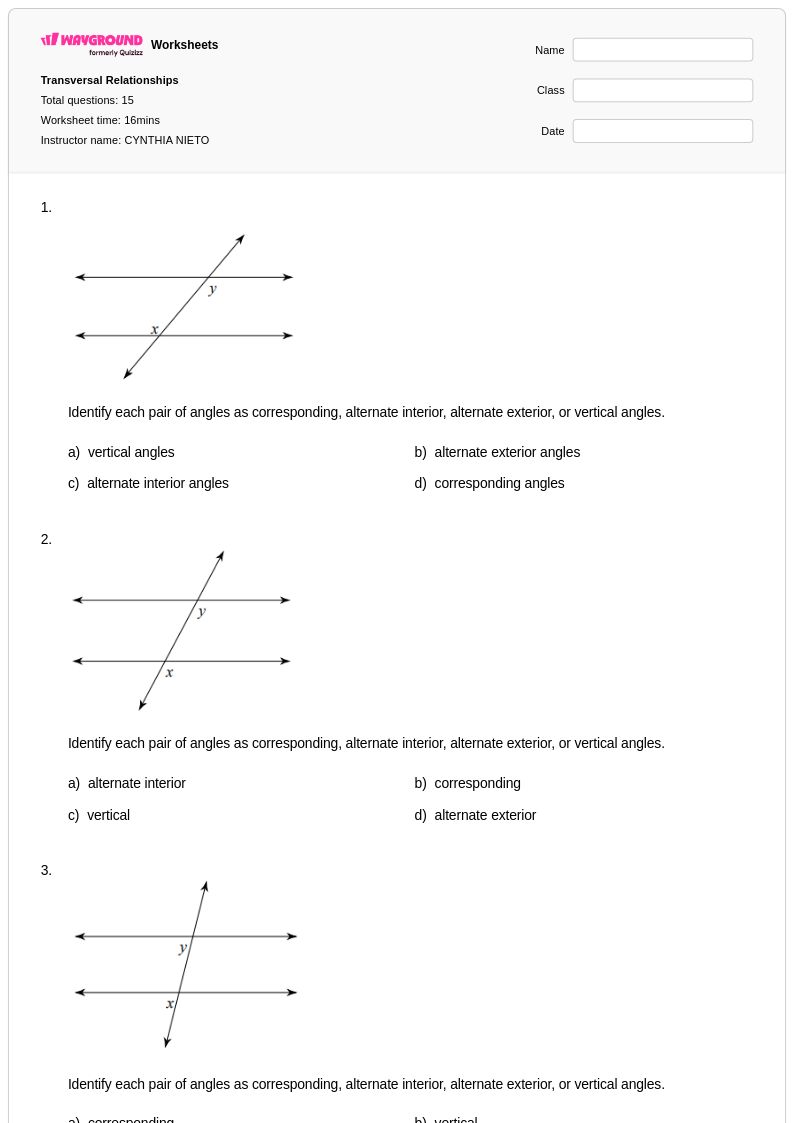
15Q
8th
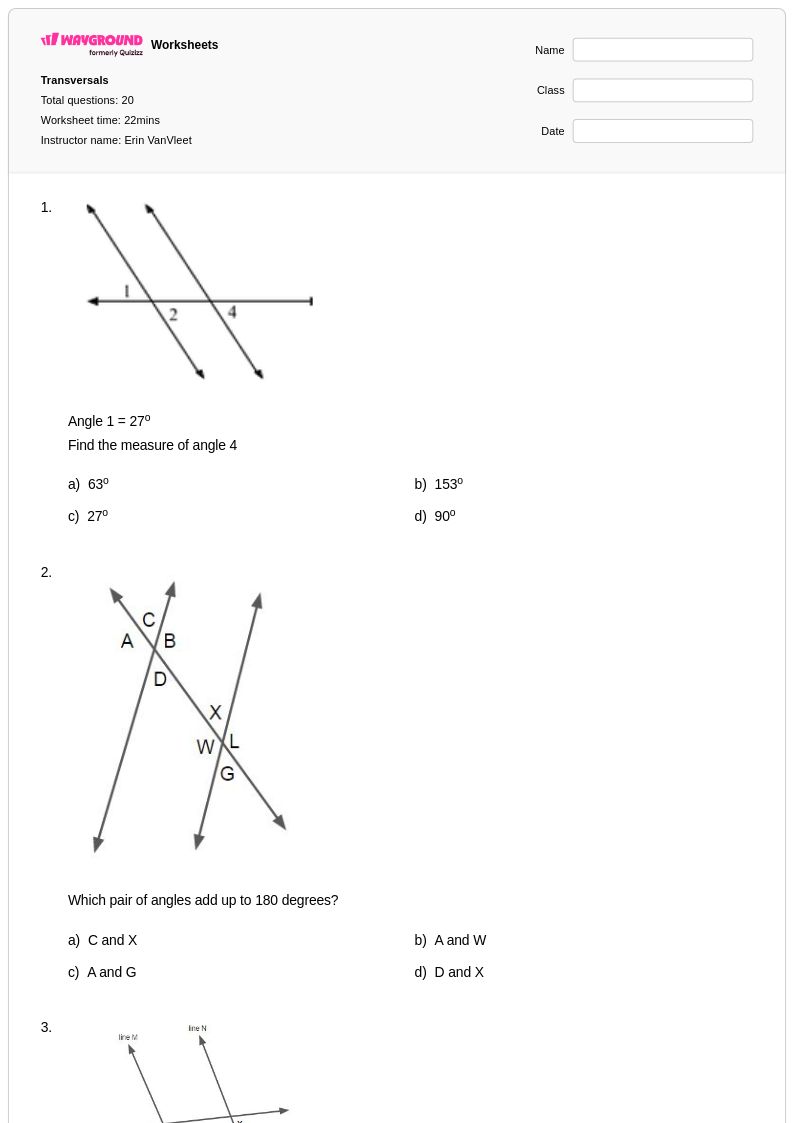
20Q
8th
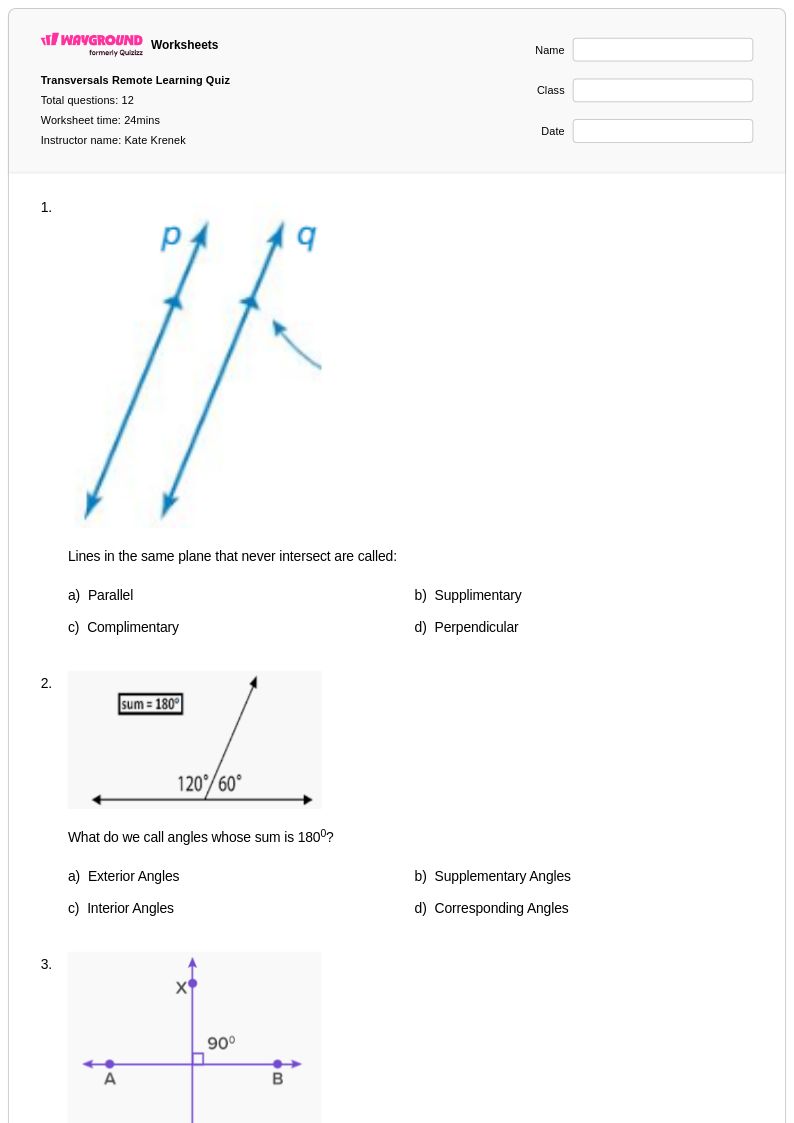
12Q
7th - 8th
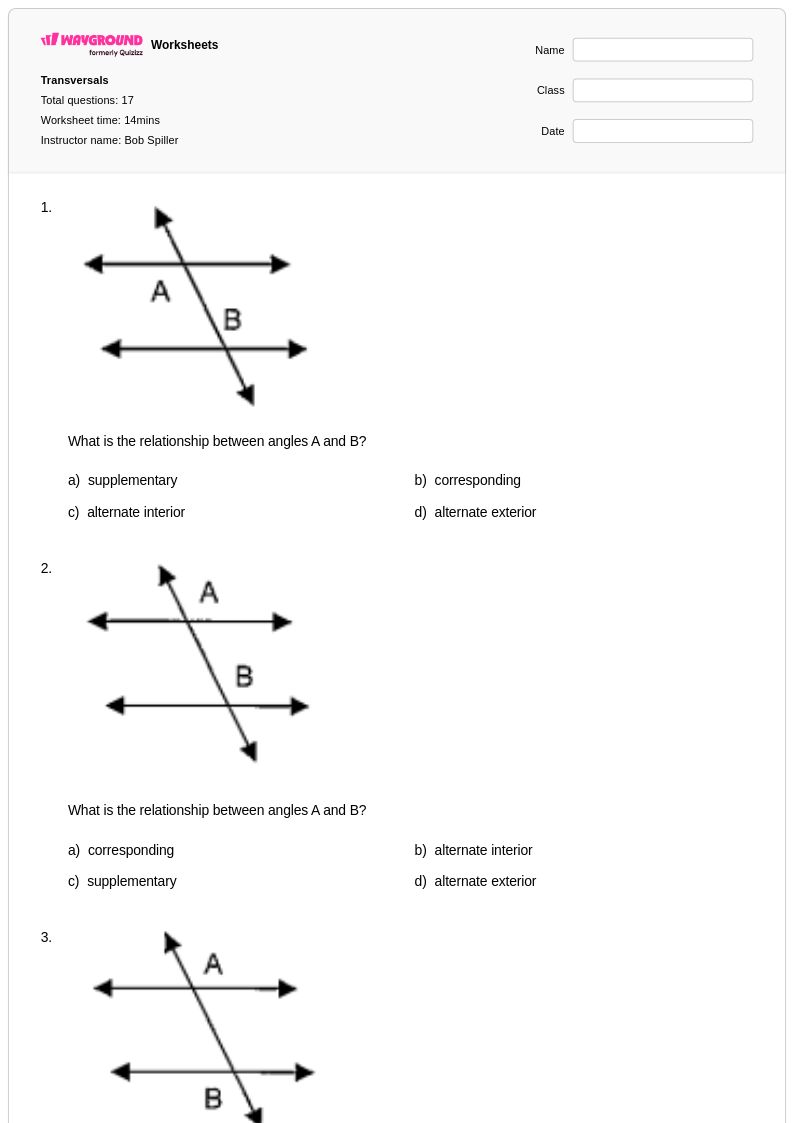
17Q
7th - 8th
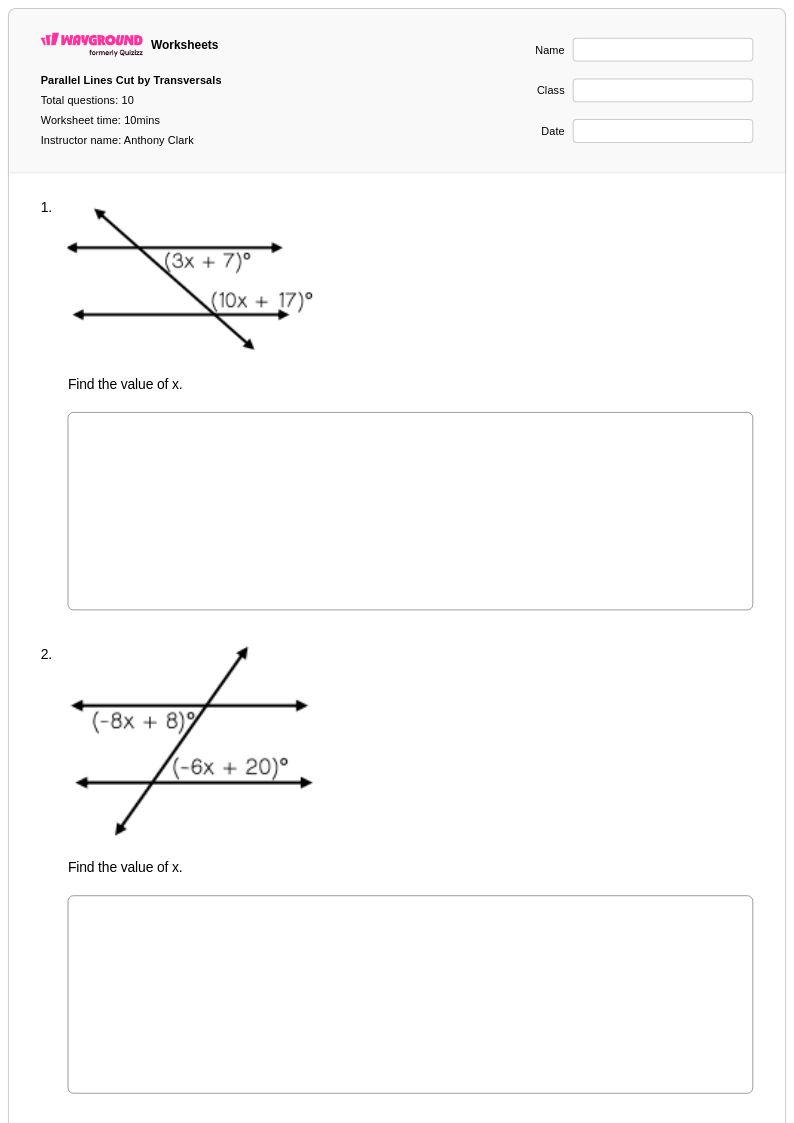
10Q
8th - Uni
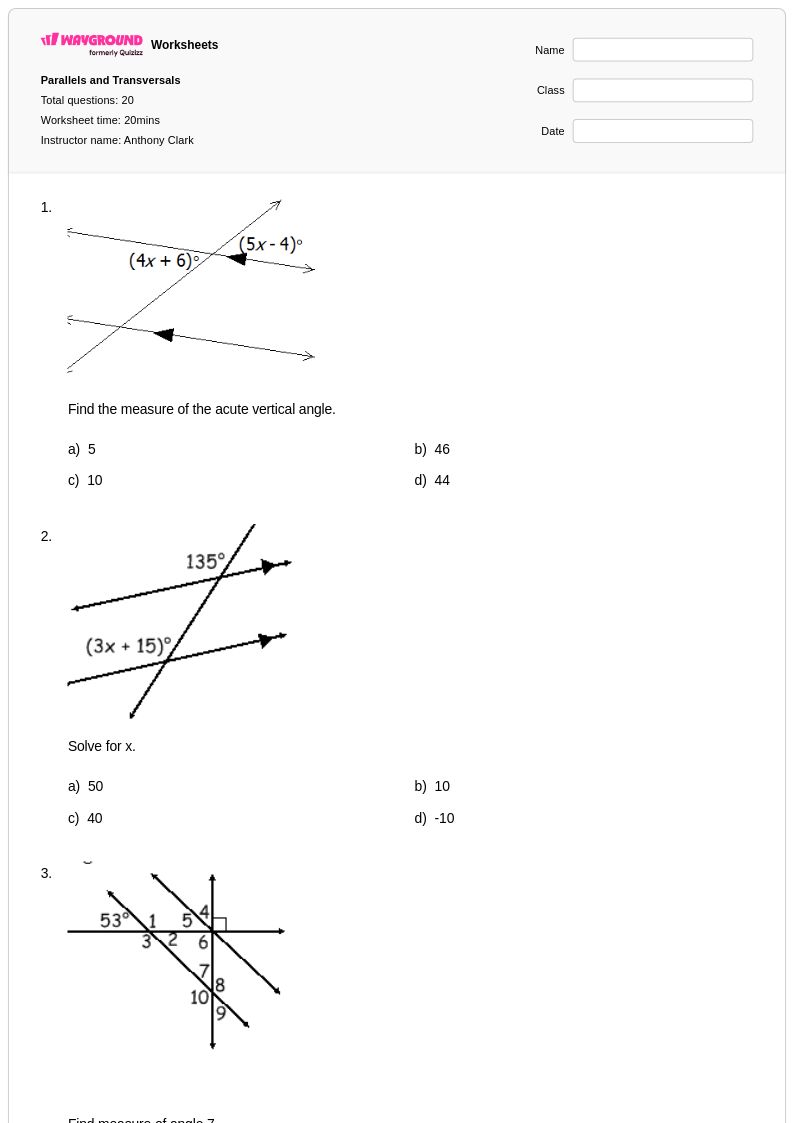
20Q
8th - Uni
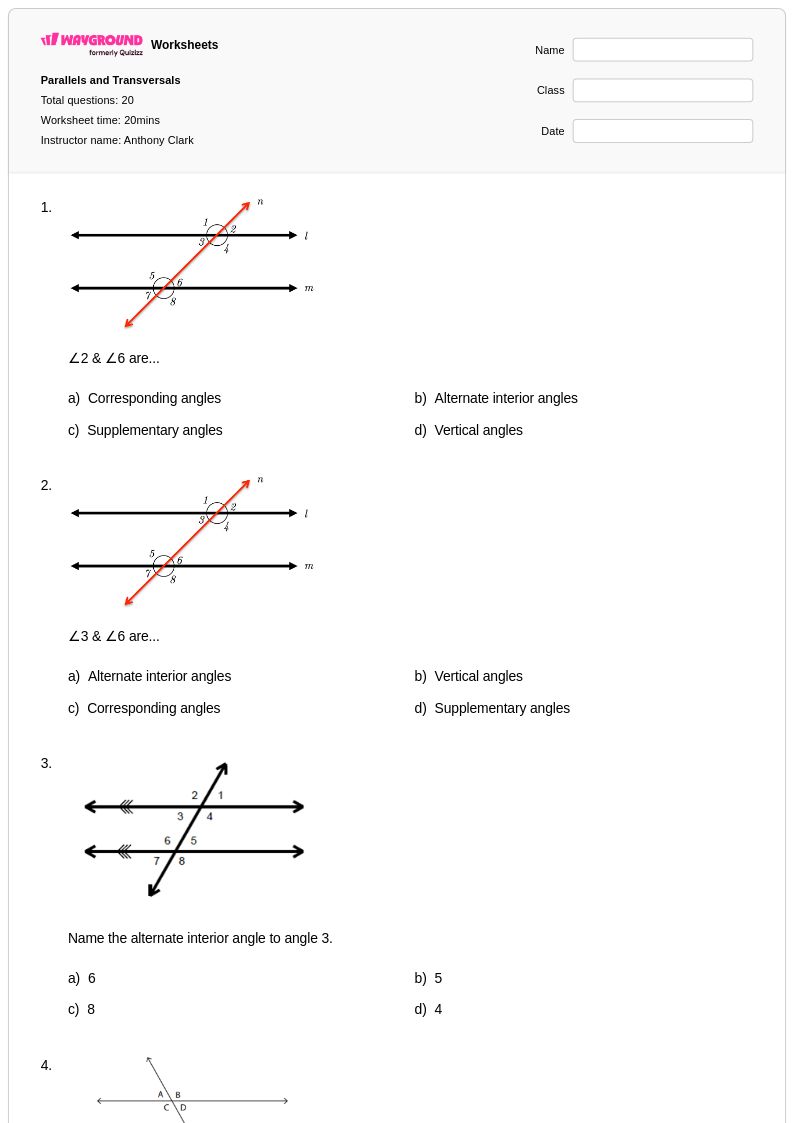
20Q
8th - Uni
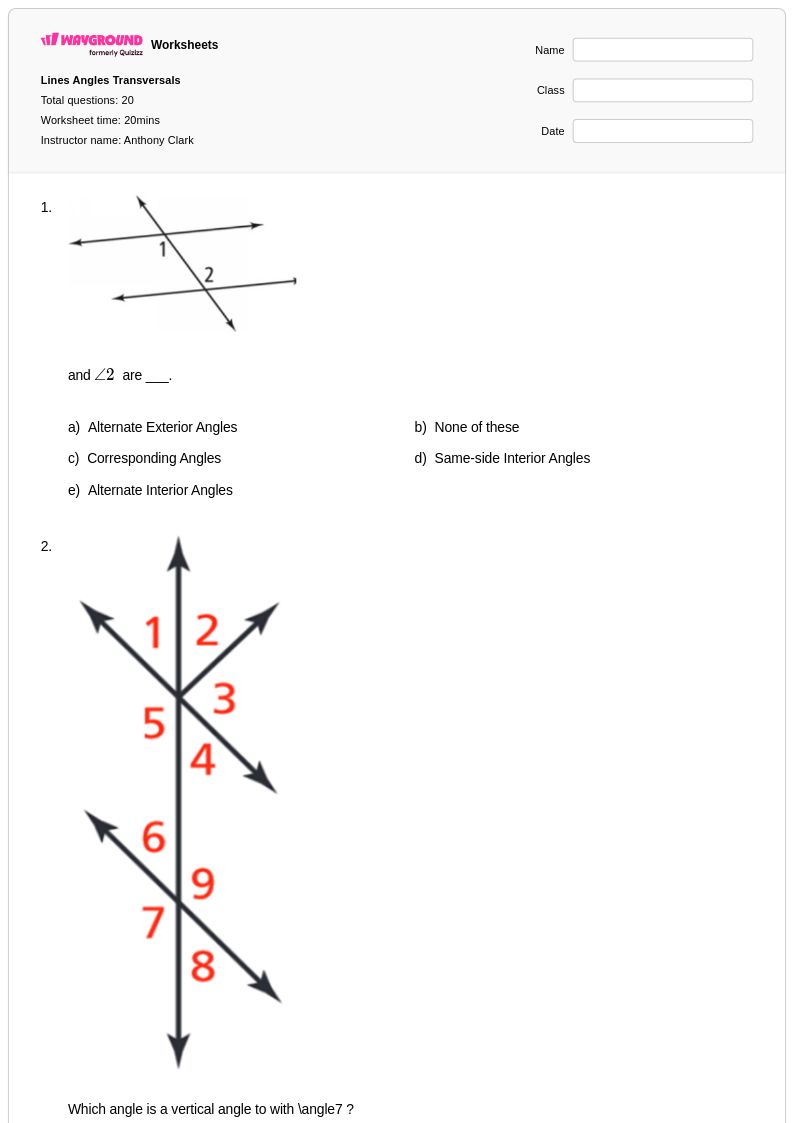
20Q
8th - Uni
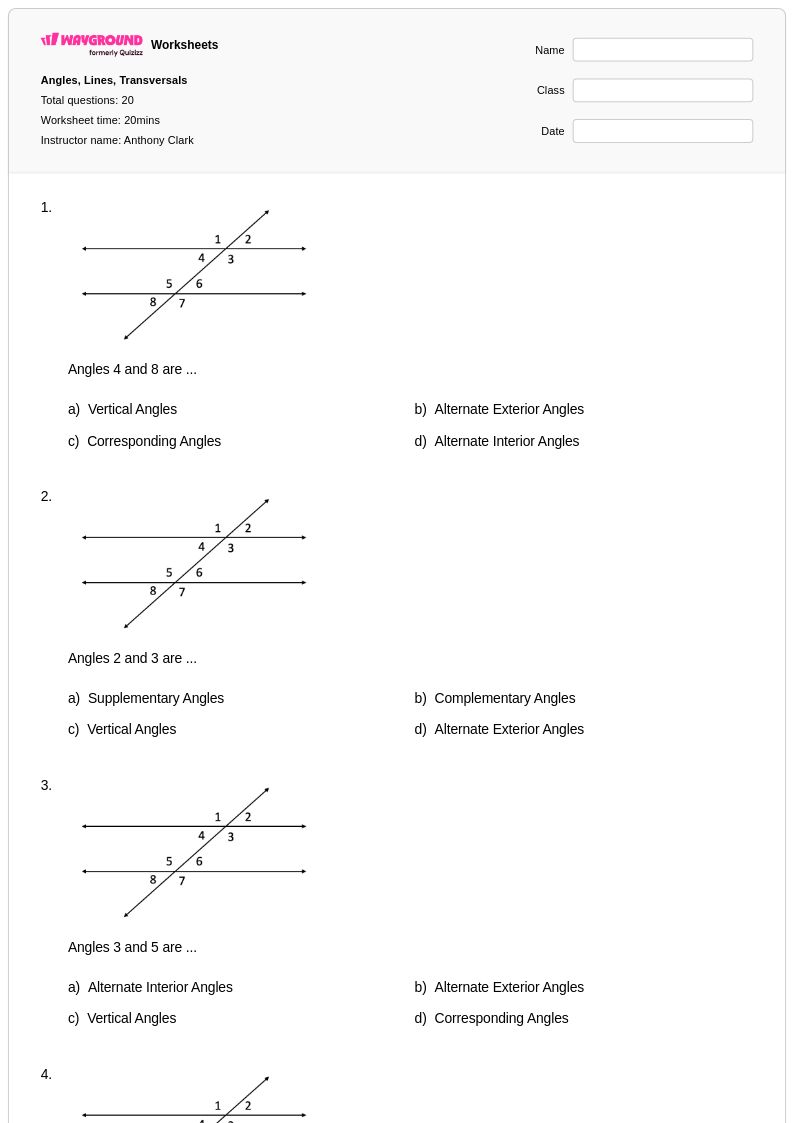
20Q
8th - Uni
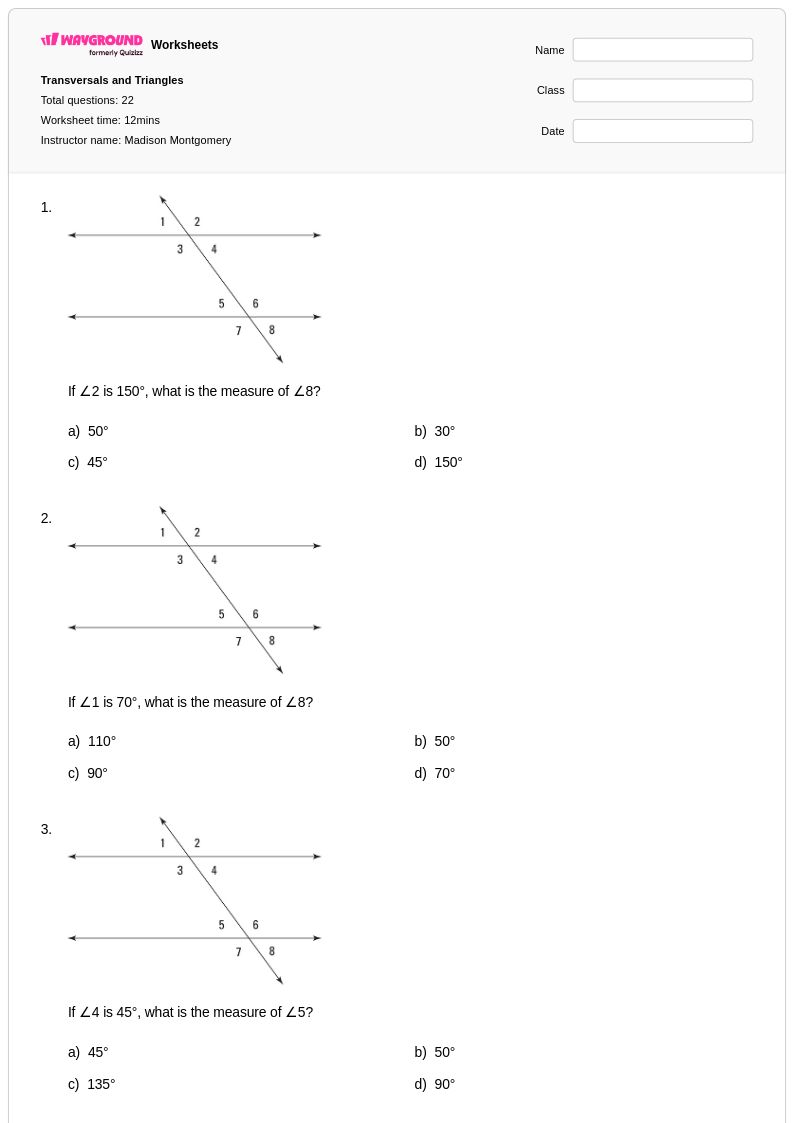
22Q
8th

10Q
8th
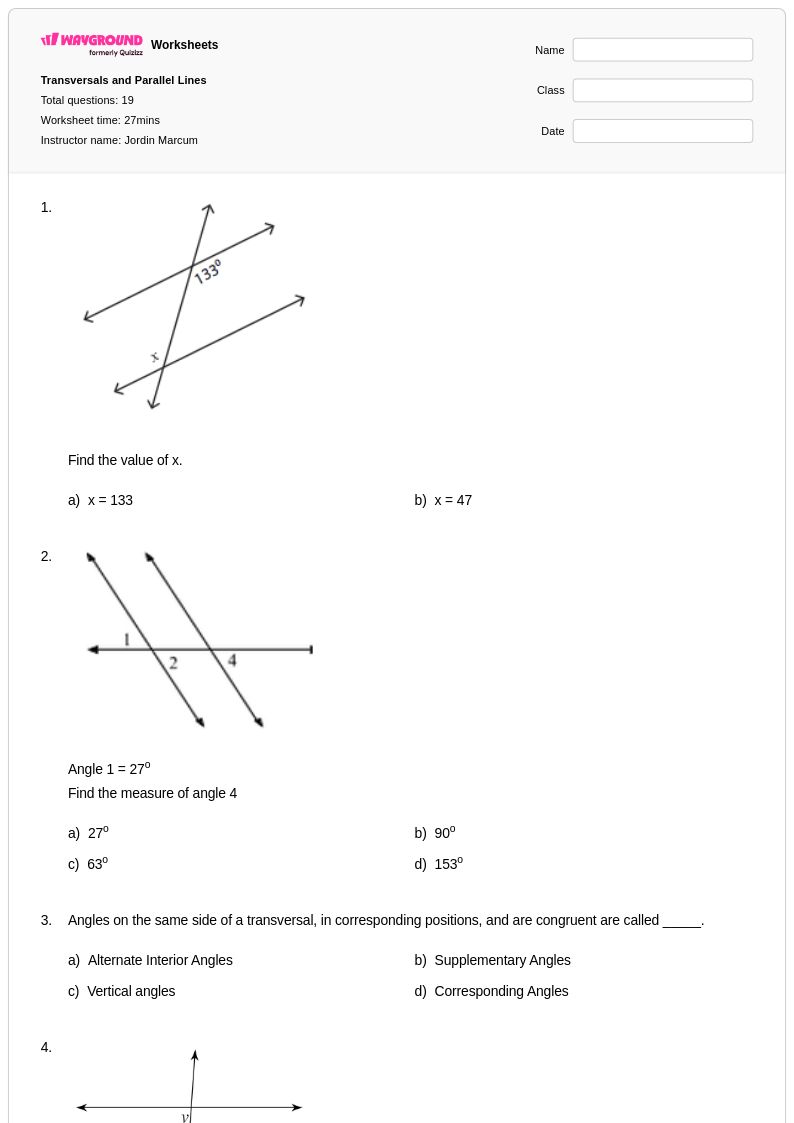
19Q
8th
20Q
6th - 8th

10Q
8th - 12th

9Q
8th
Explore otras hojas de trabajo de materias para ระดับ 8
สำรวจแผ่นงาน เส้นขวาง ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 8
เส้นตัดขวางในเรขาคณิตระดับชั้น ม.2 เป็นแนวคิดพื้นฐานที่นักเรียนจะได้สำรวจความสัมพันธ์ที่เกิดขึ้นเมื่อเส้นตรงตัดกับเส้นตรงอื่นสองเส้นขึ้นไป ซึ่งก่อให้เกิดรูปแบบมุมที่สำคัญซึ่งเป็นพื้นฐานสำหรับการให้เหตุผลทางเรขาคณิตขั้นสูง ชุดแบบฝึกหัดเส้นตัดขวางที่ครอบคลุมของ Wayground ช่วยให้นักเรียนชั้น ม.2 ได้ฝึกฝนอย่างเป็นระบบในการระบุมุมที่สมนัยกัน มุมภายในและมุมภายนอกสลับกัน และมุมภายในด้านเดียวกัน พร้อมทั้งพัฒนาความเชี่ยวชาญในการประยุกต์ใช้ความสัมพันธ์เหล่านี้เพื่อหาค่ามุมที่ไม่ทราบค่า แบบฝึกหัดที่จัดทำขึ้นอย่างรอบคอบเหล่านี้ช่วยเสริมสร้างความสามารถของนักเรียนในการจดจำความสัมพันธ์ของเส้นขนาน การใช้ทฤษฎีบทเกี่ยวกับมุม และการสร้างเหตุผลทางคณิตศาสตร์ที่สมเหตุสมผล โดยแบบฝึกหัดแต่ละชุดมีเฉลยคำตอบโดยละเอียดและสามารถดาวน์โหลดได้ฟรีในรูปแบบ PDF ที่สะดวกต่อการใช้งานทั้งในห้องเรียนและการเรียนรู้ด้วยตนเอง
คลังข้อมูลขนาดใหญ่ของ Wayground รวบรวมทรัพยากรนับล้านที่สร้างขึ้นโดยครูผู้สอนโดยเฉพาะเพื่อสนับสนุนการสอนเส้นตัดขวางในชั้น ม.2 โดยมีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพ ช่วยให้ครูผู้สอนค้นหาแบบฝึกหัดที่สอดคล้องกับวัตถุประสงค์การเรียนรู้และมาตรฐานหลักสูตรที่เฉพาะเจาะจงได้ เครื่องมือปรับระดับความยากง่ายของแพลตฟอร์มนี้ช่วยให้ครูสามารถปรับแต่งความซับซ้อนของเนื้อหาและประเภทของปัญหาให้ตรงกับความต้องการที่หลากหลายของนักเรียน ไม่ว่าจะเป็นการให้แบบฝึกหัดพื้นฐานสำหรับนักเรียนที่เรียนรู้ช้า หรือกิจกรรมเสริมที่ท้าทายสำหรับนักเรียนที่เรียนรู้เร็ว แบบฝึกหัดเหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่สามารถพิมพ์ได้และเวอร์ชันดิจิทัลแบบโต้ตอบ ซึ่งสนับสนุนแนวทางการวางแผนบทเรียนที่ยืดหยุ่น การแก้ไขทักษะการให้เหตุผลทางเรขาคณิตอย่างตรงจุด และการฝึกฝนทักษะอย่างต่อเนื่องที่สร้างความมั่นใจให้กับนักเรียนในการวิเคราะห์ความสัมพันธ์ของมุมและคุณสมบัติของเส้นขนาน ซึ่งเป็นสิ่งสำคัญสำหรับความสำเร็จในวิชาเรขาคณิตระดับมัธยมปลาย
