22Q
1st

12Q
1st - 6th
8Q
1st

17Q
5th

18Q
11th

25Q
6th

29Q
5th

12Q
4th - 6th
7Q
2nd
20Q
1st

15Q
5th

19Q
1st

16Q
5th - 10th

10Q
4th

13Q
1st - Uni

8Q
10th

20Q
1st - 5th

15Q
7th

16Q
6th
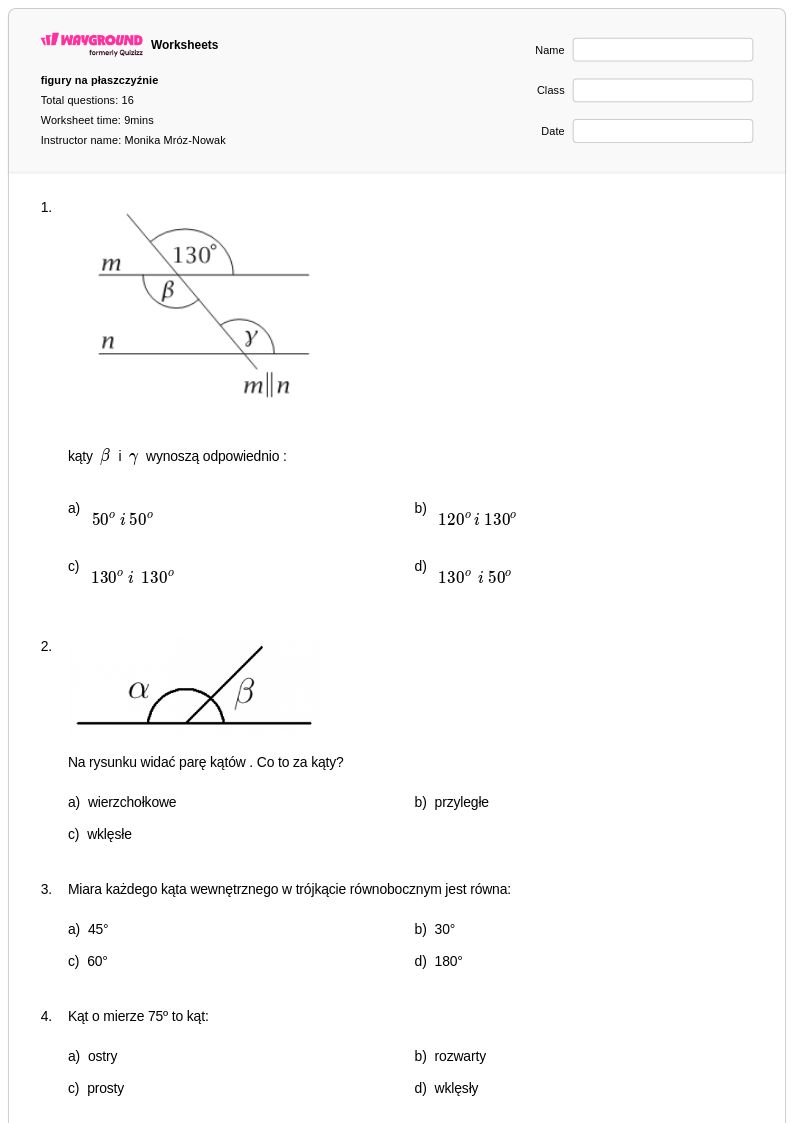
16Q
5th - 6th
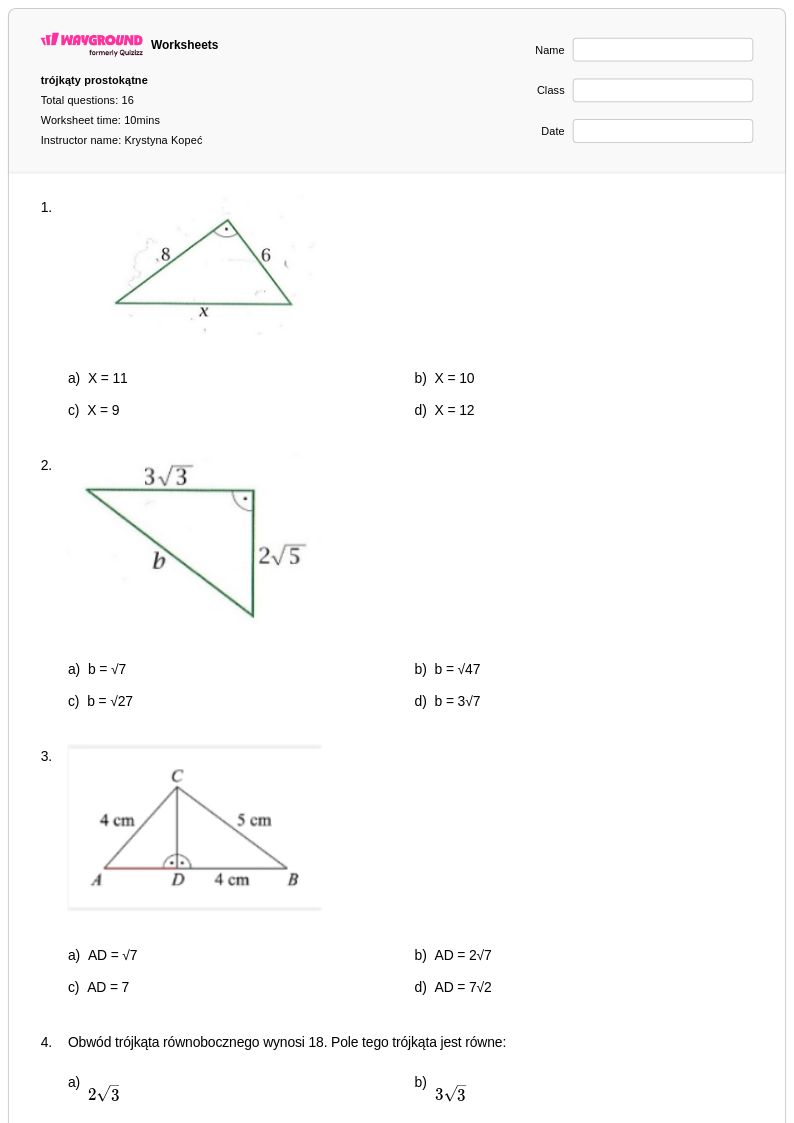
16Q
8th
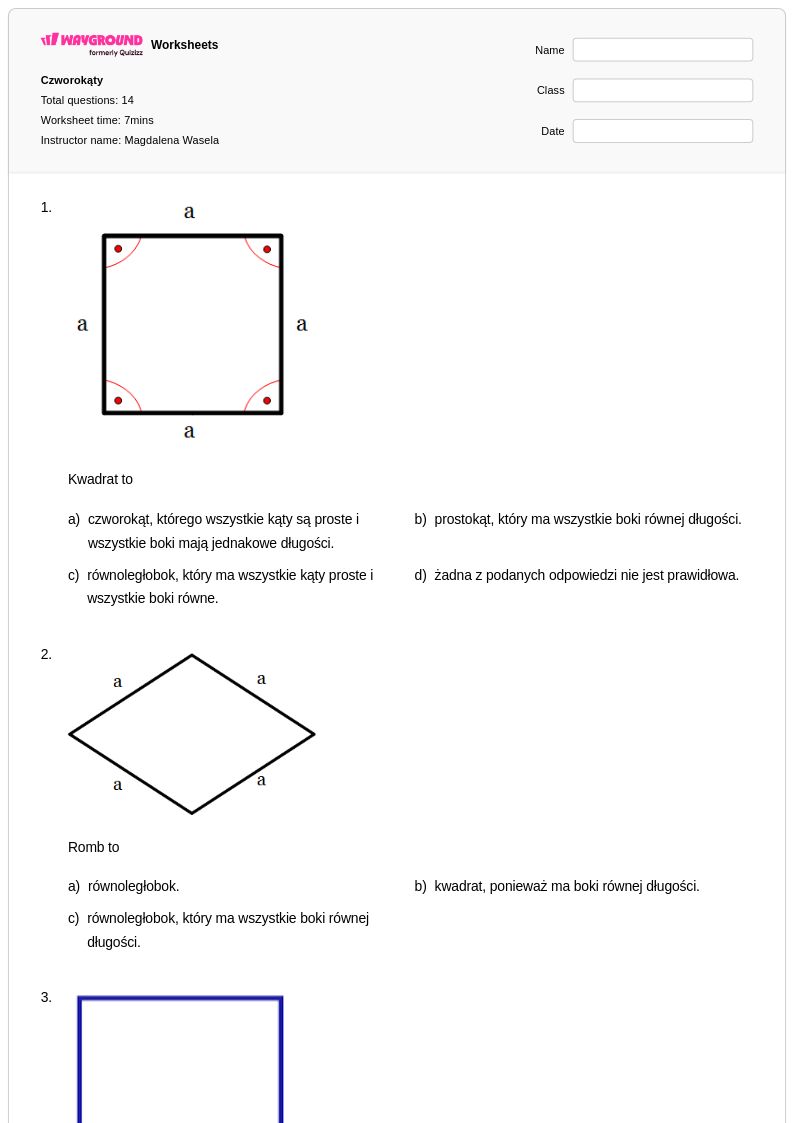
14Q
5th

13Q
6th

17Q
5th
Explore planilhas por assuntos
Przeglądaj arkusze robocze Przecięcie linii równoległych do wydrukowania
Arkusze ćwiczeń z zakresu prostych poprzecznych i równoległych, dostępne w Wayground (dawniej Quizizz), zapewniają kompleksowe ćwiczenia z zakresu jednego z najbardziej fundamentalnych pojęć geometrii. Te profesjonalnie zaprojektowane zasoby pomagają uczniom opanować zależności między kątami powstającymi, gdy prosta poprzeczna przecina dwie proste równoległe, w tym kąty odpowiadające, kąty naprzemienne wewnętrzne i zewnętrzne oraz kąty współwewnętrzne. Arkusze ćwiczeń wzmacniają umiejętności krytycznego rozumowania geometrycznego poprzez systematyczne zadania praktyczne, które obejmują zarówno identyfikację podstawowych zależności między kątami, jak i rozwiązywanie złożonych, wieloetapowych zadań z wyrażeniami algebraicznymi. Każdy arkusz ćwiczeń zawiera szczegółowy klucz odpowiedzi i jest dostępny w darmowym pliku PDF do wydruku, co ułatwia nauczycielom włączenie tych cennych materiałów do planów lekcji i zadań domowych.
Wayground (dawniej Quizizz) zapewnia nauczycielom matematyki dostęp do milionów zasobów stworzonych przez nauczycieli, skupiających się na pojęciach prostych poprzecznych i równoległych. Rozbudowane funkcje wyszukiwania i filtrowania platformy pozwalają nauczycielom szybko znaleźć arkusze ćwiczeń zgodne ze standardami programowymi i dopasowane do specyficznych potrzeb edukacyjnych uczniów. Nauczyciele mogą łatwo różnicować metody nauczania, wybierając arkusze ćwiczeń o różnym poziomie trudności, dostosowywać dostępne materiały do wymagań swojej klasy oraz korzystać z zasobów w formatach do druku i cyfrowych, w tym plików PDF do pobrania. Te wszechstronne narzędzia wspomagają kompleksowe planowanie lekcji, oferując jednocześnie ukierunkowane opcje korepetycji, zajęć wzbogacających i ciągłego doskonalenia umiejętności, które pomagają uczniom budować pewność siebie w rozwiązywaniu problemów geometrycznych.
