
18 Q
8th - 9th

20 Q
KG
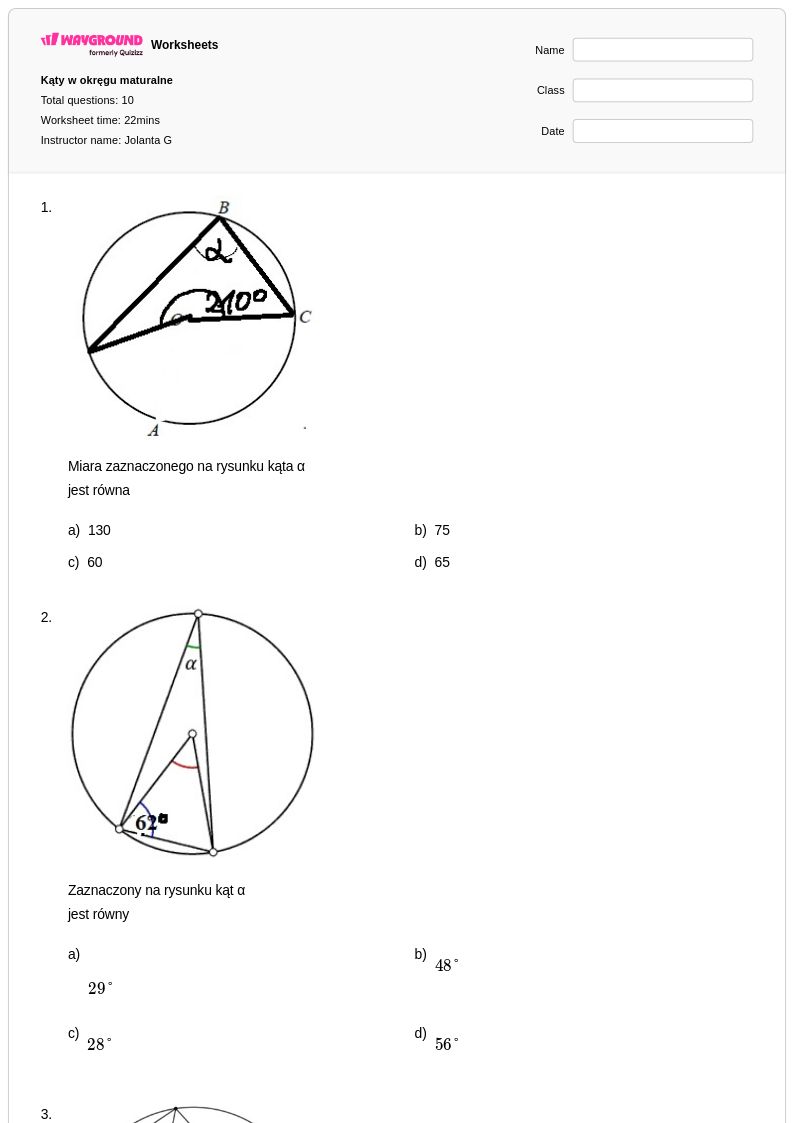
10 Q
1st

10 Q
6th

18 Q
7th - 8th

20 Q
10th - 12th

13 Q
2nd

10 Q
3rd

19 Q
8th

29 Q
KG

14 Q
8th

12 Q
10th
10 Q
1st
10 Q
8th

19 Q
7th
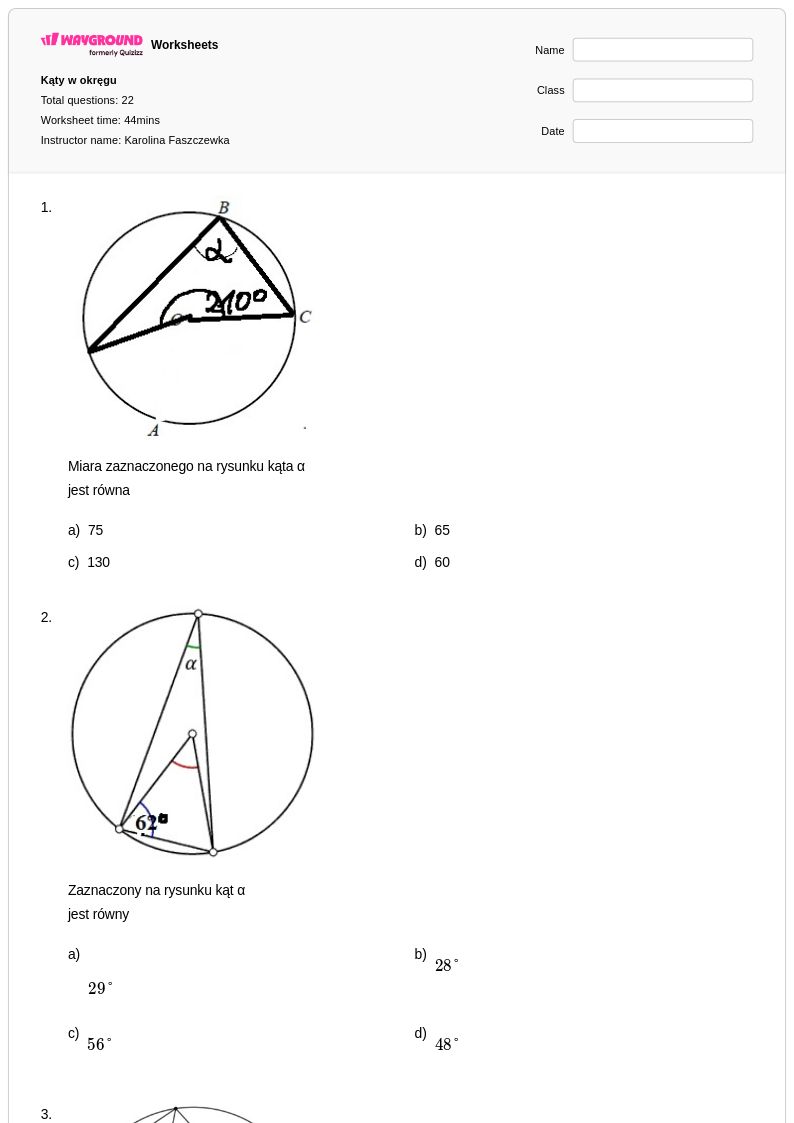
22 Q
KG
10 Q
4th

32 Q
10th

17 Q
2nd

10 Q
10th

11 Q
KG

21 Q
9th - 12th

19 Q
7th

13 Q
11th
Explore Worksheets by Subjects
Przeglądaj arkusze robocze Twierdzenia o okręgu do wydrukowania
Arkusze ćwiczeń z twierdzeniami o okręgach dostępne w Wayground (dawniej Quizizz) zapewniają uczniom wszechstronne możliwości praktycznego opanowania podstawowych zależności i własności w obrębie okręgów. Te profesjonalnie zaprojektowane zasoby matematyczne wzmacniają umiejętności krytycznego rozumowania geometrycznego, angażując uczniów w rozwiązywanie problemów dotyczących kątów wpisanych, kątów środkowych, zależności styczna-sieczna oraz czworokątów wpisanych. Każdy zbiór arkuszy ćwiczeń zawiera szczegółowe klucze odpowiedzi i rozwiązania krok po kroku, które prowadzą uczniów przez złożone zastosowania twierdzeń, a darmowy format PDF do wydruku zapewnia łatwą dystrybucję w klasie i samodzielną naukę. Zadania praktyczne systematycznie budują zrozumienie kluczowych pojęć, takich jak twierdzenie o kącie w półkolu, twierdzenie o odcinku naprzemiennym oraz związek między kątami opartymi na tym samym łuku.
Wayground (dawniej Quizizz) udostępnia nauczycielom matematyki miliony stworzonych przez nich zasobów dotyczących twierdzeń o okręgach, które usprawniają planowanie lekcji i wspierają zróżnicowane nauczanie. Rozbudowane funkcje wyszukiwania i filtrowania platformy pozwalają nauczycielom szybko znaleźć arkusze ćwiczeń zgodne z określonymi standardami programowymi i poziomami umiejętności, a narzędzia personalizacji umożliwiają modyfikację istniejących materiałów w celu dopasowania ich do indywidualnych potrzeb klasy. Te obszerne zbiory są dostępne zarówno w formacie do druku, jak i cyfrowym, w tym w formacie PDF do pobrania, dzięki czemu idealnie nadają się do tradycyjnych sal lekcyjnych, hybrydowych środowisk nauczania oraz nauczania zdalnego. Nauczyciele mogą skutecznie wykorzystywać te zasoby do ukierunkowanej pomocy uczniom mającym trudności w nauce, zajęć wzbogacających dla uczniów zaawansowanych oraz do regularnego ćwiczenia umiejętności, które wzmacnia opanowanie twierdzeń geometrycznych w różnych kontekstach edukacyjnych.
