
24 P
8th

6 P
5th - 8th

17 P
4th
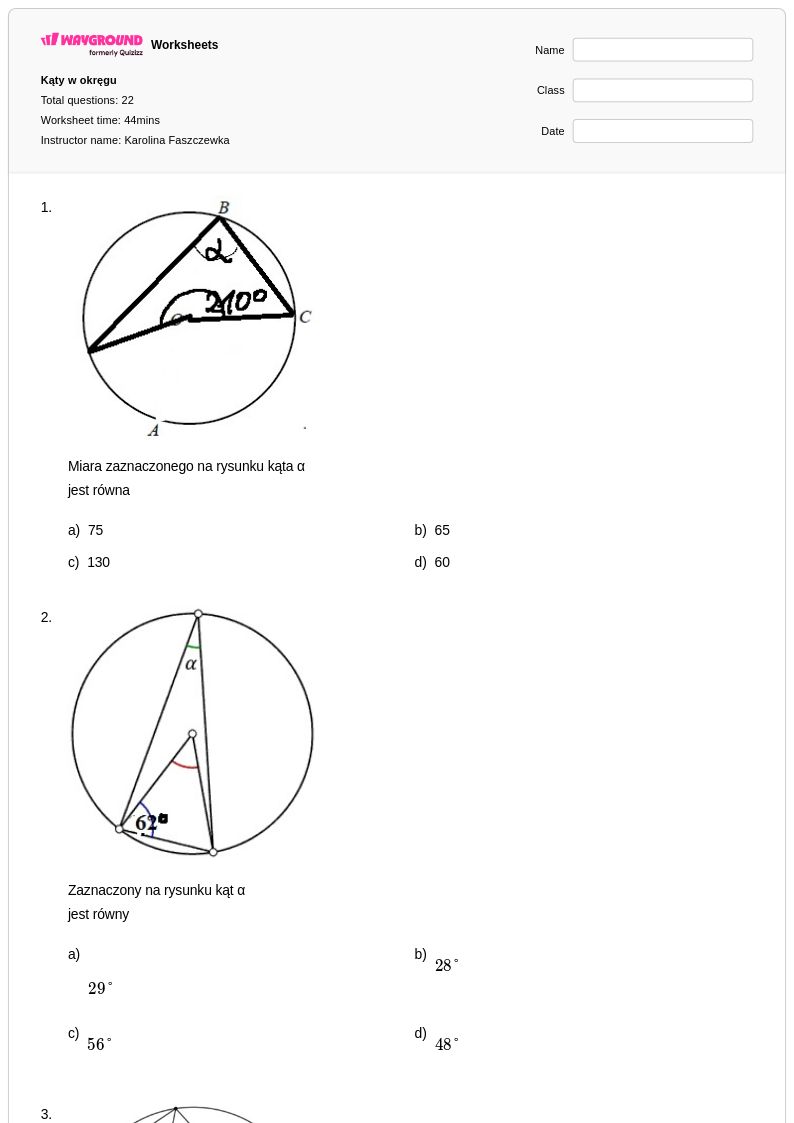
22 P
KG

19 P
1st

27 P
8th
23 P
1st - 4th

30 P
8th

11 P
8th

7 P
3rd
16 P
4th - 8th

93 P
8th

14 P
8th

36 P
8th

17 P
4th

21 P
9th - 12th

19 P
9th - 12th

20 P
6th
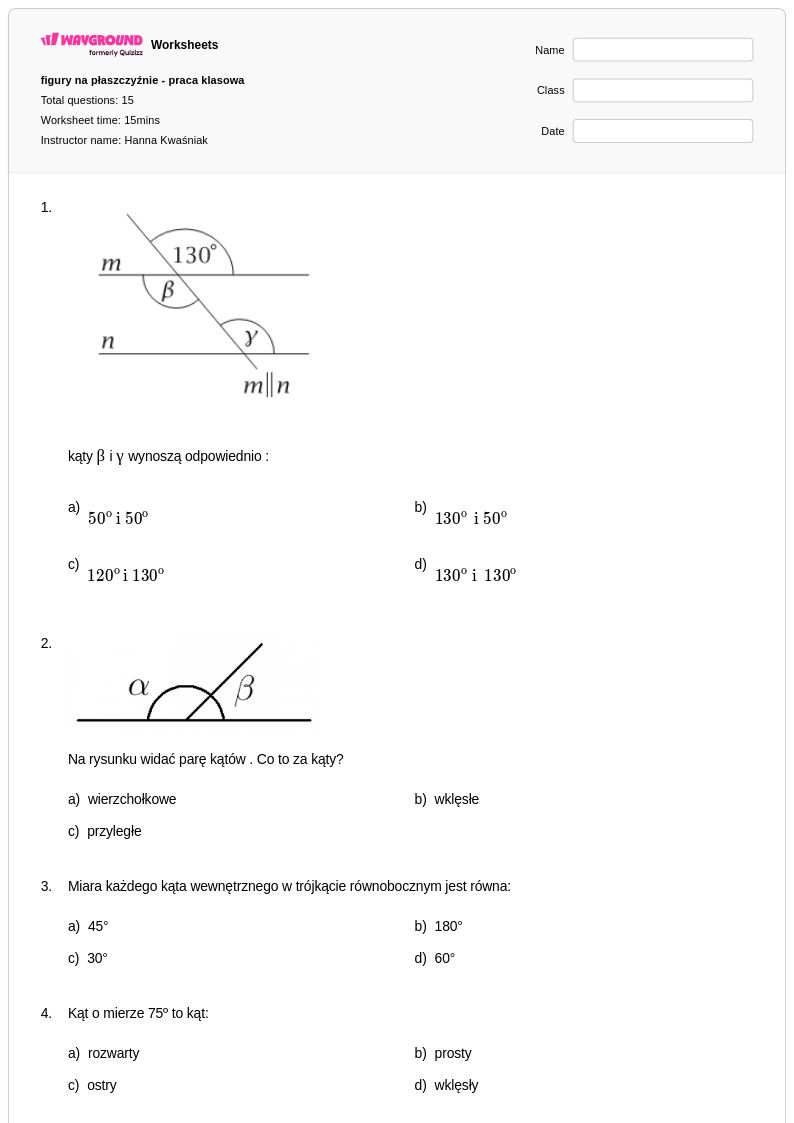
15 P
5th
15 P
KG
19 P
7th - 8th

12 P
5th

56 P
8th
20 P
12th
Przeglądaj arkusze według tematów
Przeglądaj arkusze robocze Twierdzenie o środkowym odcinku trapezu do wydrukowania
Twierdzenie o środku odcinka trapezu stanowi fundamentalną koncepcję geometrii, którą uczniowie muszą opanować, aby zrozumieć właściwości i zależności w czworokątach. Obszerny zbiór arkuszy ćwiczeń z twierdzenia o środku odcinka trapezu w Wayground zapewnia uczniom ukierunkowane zadania praktyczne, które wzmacniają tę podstawową zasadę geometryczną, głoszącą, że środek odcinka trapezu jest równoległy do obu podstaw, a jego długość jest równa średniej długości podstaw. Te bezpłatne, do druku materiały zawierają różnorodne ćwiczenia, od podstawowych obliczeń na środku odcinka trapezu po bardziej złożone zastosowania obejmujące geometrię współrzędnych i wyrażenia algebraiczne. Każdy arkusz ćwiczeń zawiera szczegółowy klucz odpowiedzi, który pozwala uczniom zweryfikować swoją pracę i zidentyfikować obszary do poprawy, jednocześnie budując pewność siebie w stosowaniu twierdzenia w różnych typach zadań.
Obszerna biblioteka Wayground, zawierająca miliony zasobów stworzonych przez nauczycieli, umożliwia nauczycielom efektywne wspieranie nauki uczniów poprzez starannie dobrane materiały dotyczące twierdzenia o środku odcinka trapezu. Rozbudowane funkcje wyszukiwania i filtrowania platformy umożliwiają nauczycielom szybkie znajdowanie arkuszy ćwiczeń zgodnych z określonymi standardami programowymi i różnicowanie nauczania w zależności od indywidualnych potrzeb uczniów. Niezależnie od tego, czy są one dostarczane w tradycyjnym formacie PDF do dystrybucji w klasie, czy dostępne za pośrednictwem platform cyfrowych do nauki zdalnej, te konfigurowalne zasoby zapewniają elastyczność w różnych środowiskach nauczania. Nauczyciele mogą bezproblemowo integrować te materiały z planowaniem lekcji na etapie nauczania początkowego, ukierunkowanymi działaniami naprawczymi dla uczniów mających trudności z nauką lub ćwiczeniami wzbogacającymi dla uczniów zaawansowanych, zapewniając każdemu uczniowi solidne zrozumienie zastosowania twierdzenia o środkowym odcinku trapezu w rzeczywistych scenariuszach rozwiązywania problemów geometrycznych.
