16Q
7th

10Q
4th

11Q
4th - 5th

8Q
6th

10Q
Uni

12Q
5th

10Q
5th - 6th

10Q
1st

17Q
KG

11Q
12th

10Q
8th
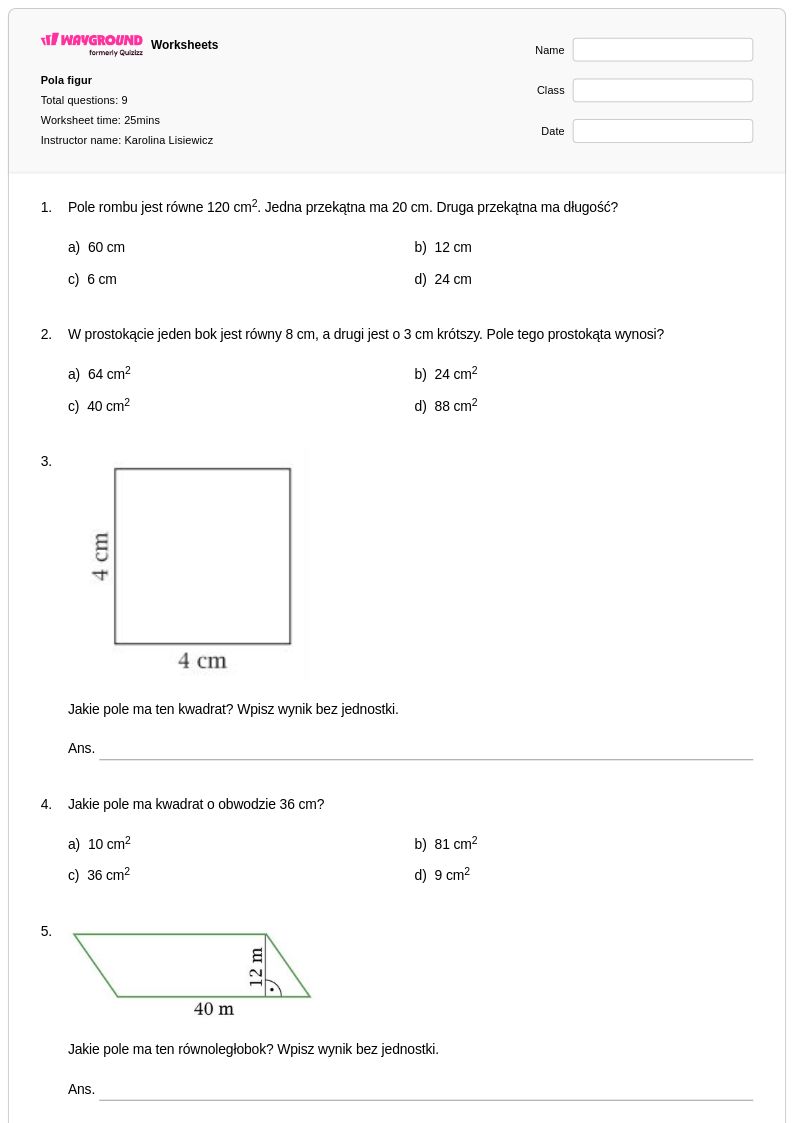
9Q
6th
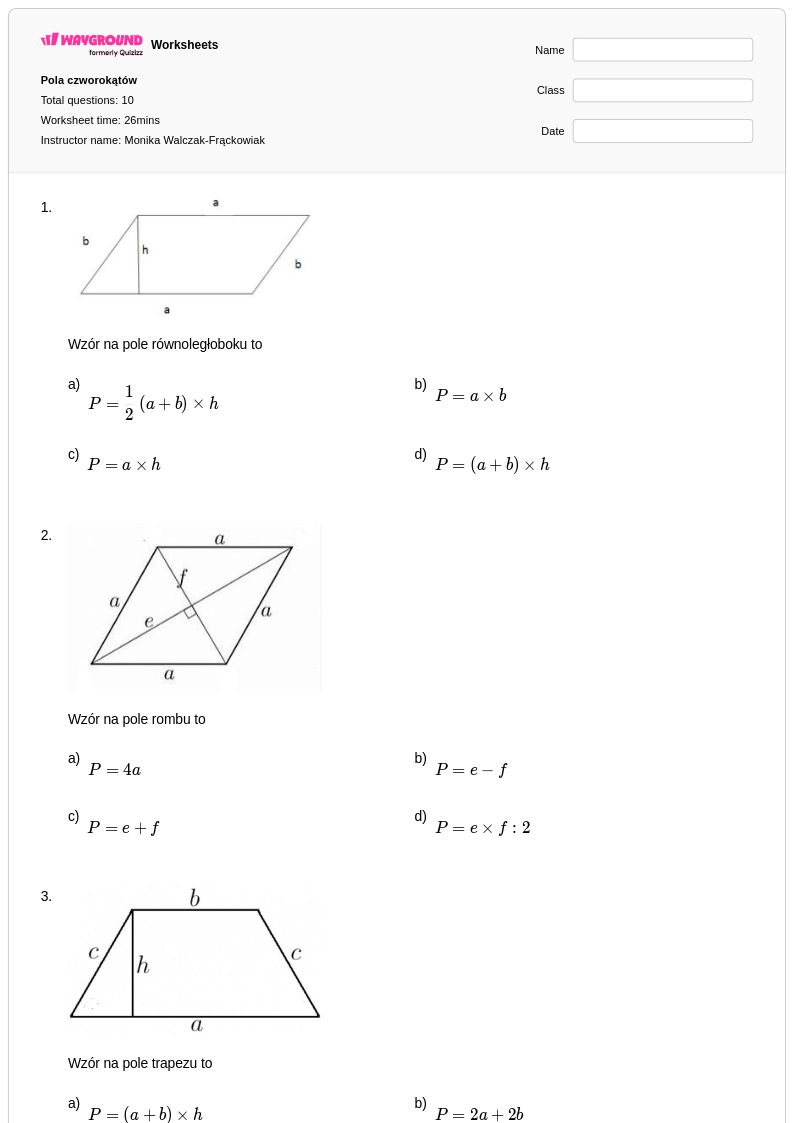
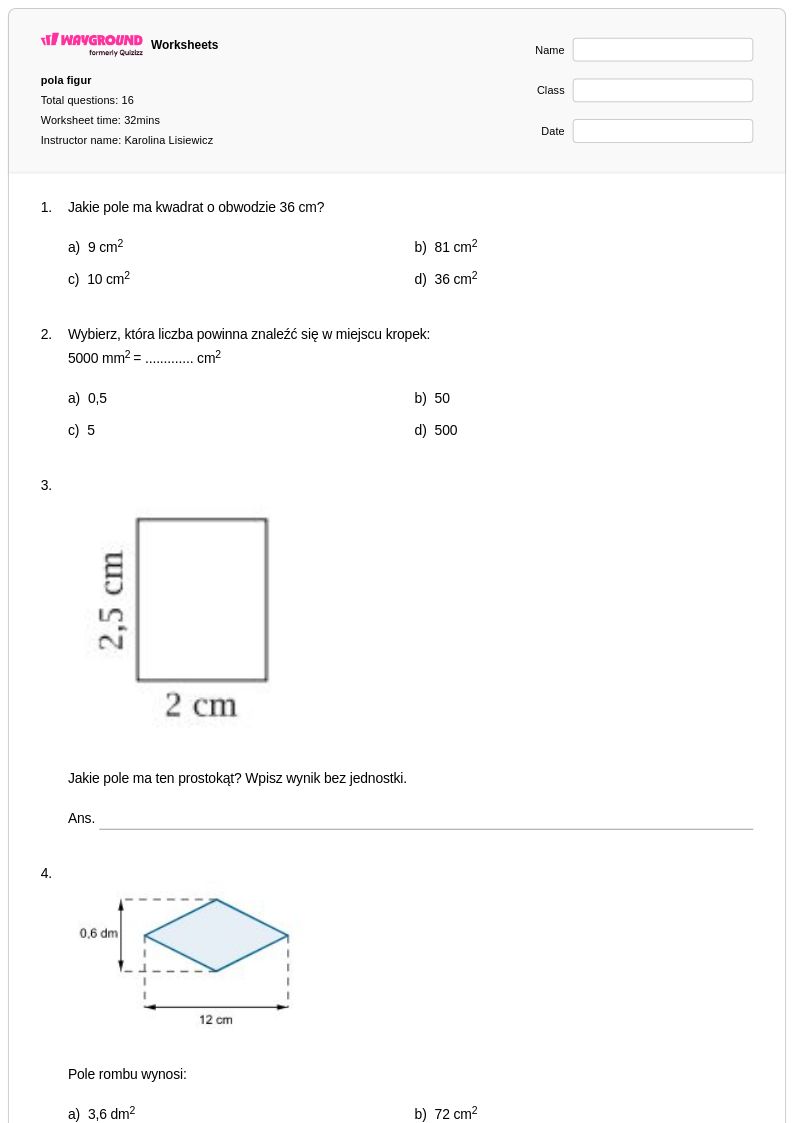
10Q
5th

16Q
KG - PD

10Q
7th
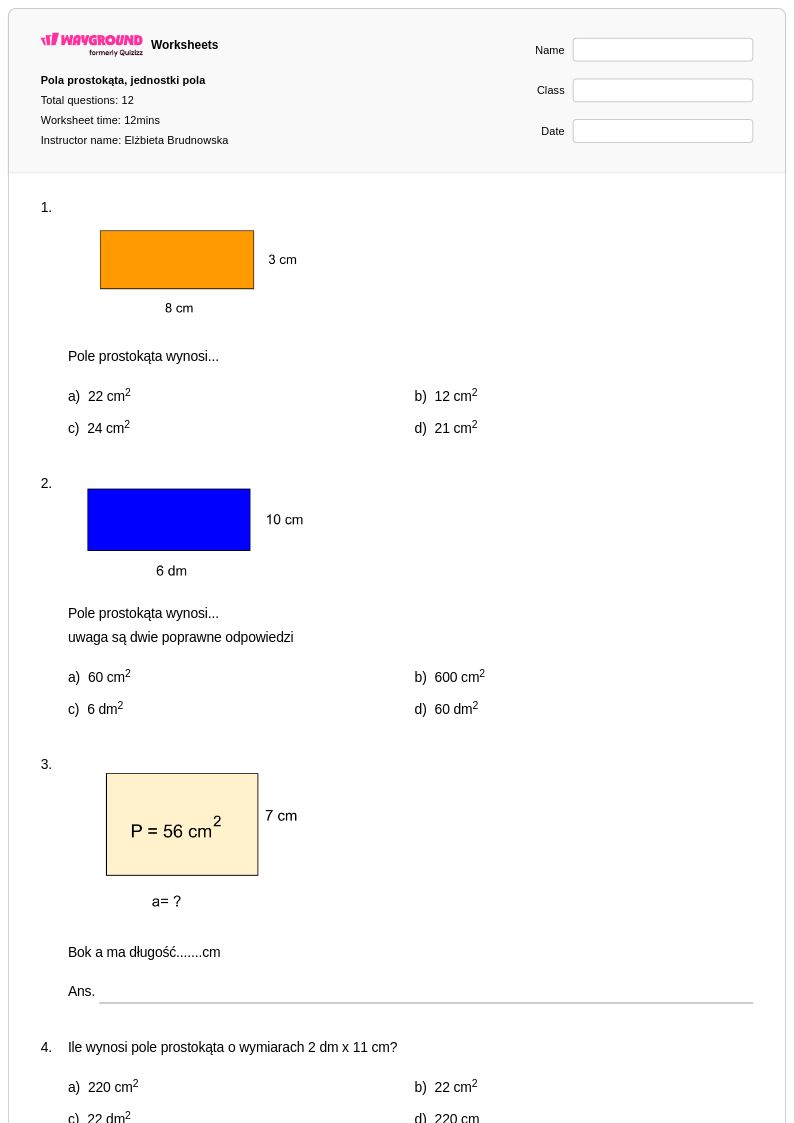
12Q
6th - Uni

13Q
8th

6Q
1st - 5th

13Q
6th - 7th
35Q
8th

10Q
Uni

21Q
KG

13Q
6th

7Q
5th
Explorar hojas de trabajo por materias
Przeglądaj arkusze robocze Pole półkola do wydrukowania
Arkusze ćwiczeń z pola półkola dostępne w Wayground (dawniej Quizizz) zapewniają uczniom wszechstronne możliwości praktycznego opanowania tej fundamentalnej koncepcji geometrycznej. Te starannie zaprojektowane zasoby edukacyjne koncentrują się na rozwijaniu umiejętności obliczania pola półkoli za pomocą wzoru A = (πr²)/2, jednocześnie wzmacniając ich zrozumienie relacji między okręgami a półkolami. Zbiory arkuszy ćwiczeń zawierają różnorodne zadania praktyczne, które obejmują zarówno podstawowe obliczenia z podanymi promieniami, jak i bardziej złożone zastosowania praktyczne, obejmujące ogrody półkoliste, okna i elementy architektoniczne. Każdy arkusz ćwiczeń zawiera szczegółowy klucz odpowiedzi, który wspiera samoocenę i weryfikację wiedzy. Materiały są dostępne jako bezpłatne materiały do druku w wygodnym formacie PDF, zarówno do zajęć w klasie, jak i do samodzielnej nauki.
Wayground (dawniej Quizizz) zapewnia nauczycielom matematyki dostęp do milionów zasobów stworzonych przez nauczycieli, specjalnie zaprojektowanych do nauczania geometrii, w tym do obszernych zbiorów materiałów do ćwiczeń z pola półkoła. Rozbudowane funkcje wyszukiwania i filtrowania platformy umożliwiają nauczycielom szybkie wyszukiwanie arkuszy ćwiczeń zgodnych z określonymi standardami programowymi i odpowiadających poziomowi umiejętności uczniów. Zaawansowane narzędzia różnicujące pozwalają nauczycielom dostosowywać zadania poprzez dostosowywanie poziomów trudności, dodawanie pomocy wizualnych lub modyfikowanie kontekstów zadań, aby sprostać zróżnicowanym potrzebom edukacyjnym. Te elastyczne zasoby są dostępne zarówno w formacie do druku, jak i cyfrowym, dzięki czemu idealnie nadają się do tradycyjnych zajęć lekcyjnych, zadań domowych, sesji naprawczych i zajęć dodatkowych. Nauczyciele mogą bezproblemowo integrować te materiały z planem lekcji, aby zapewnić ukierunkowane ćwiczenia umiejętności, ocenić zrozumienie materiału przez uczniów i wspierać indywidualne ścieżki nauczania w zakresie obliczeń geometrycznych.
