
13 คิว
8th - Uni
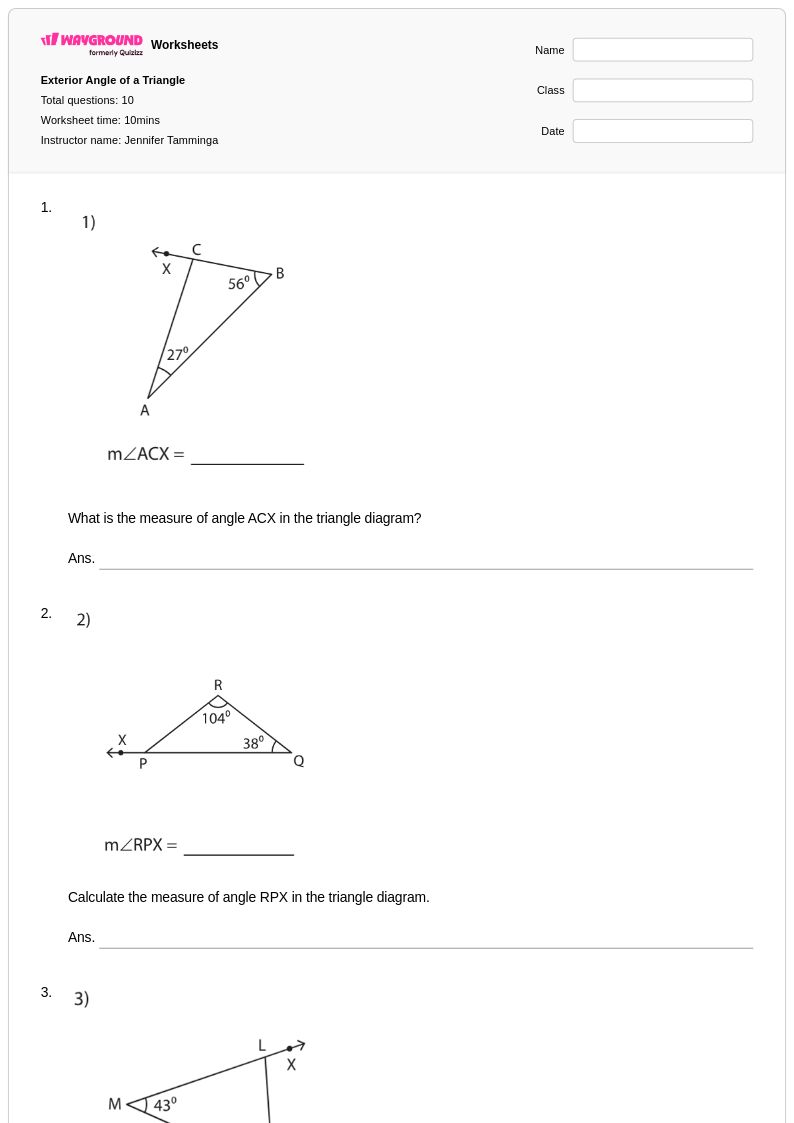
10 คิว
10th

20 คิว
9th - 12th
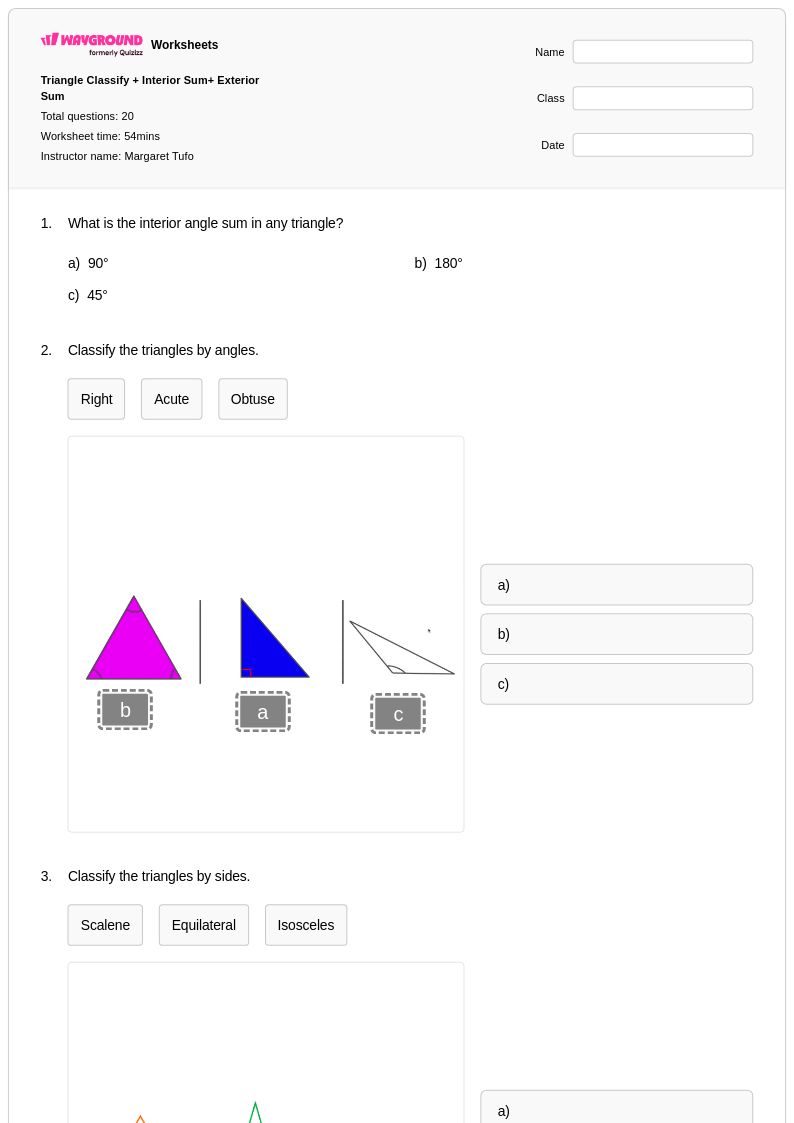
20 คิว
9th - 12th

20 คิว
8th - Uni
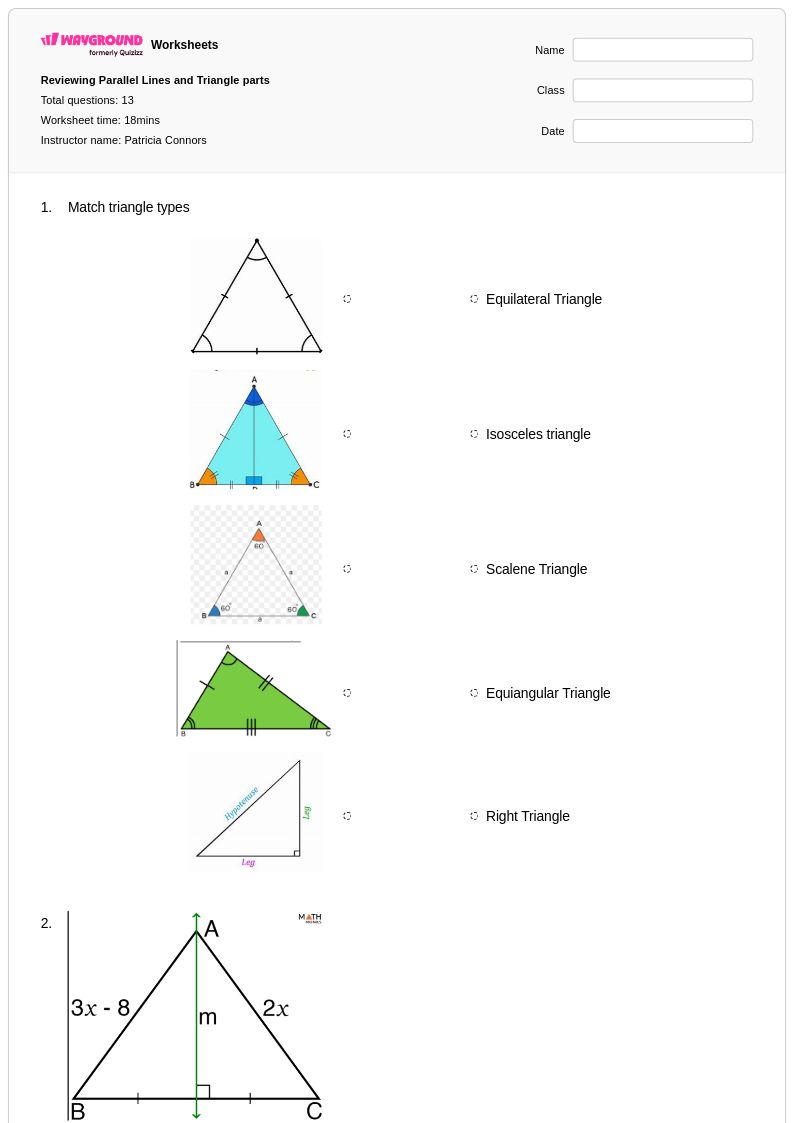
13 คิว
10th
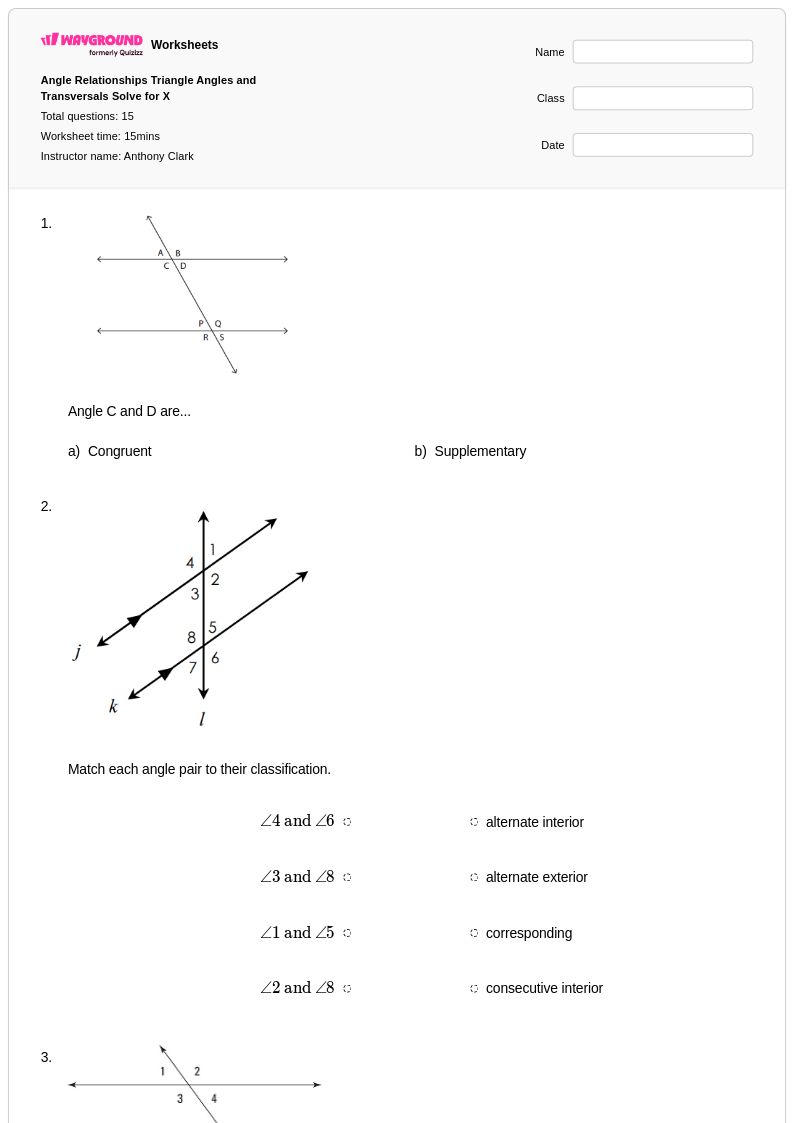
15 คิว
8th - Uni

20 คิว
8th - Uni

20 คิว
8th - Uni
20 คิว
10th - Uni
20 คิว
8th - Uni

10 คิว
10th

18 คิว
9th - 11th
18 คิว
9th - 12th
18 คิว
10th
20 คิว
8th - Uni

11 คิว
9th - 10th
11 คิว
9th - 12th
15 คิว
8th - Uni
20 คิว
9th - 12th

50 คิว
10th
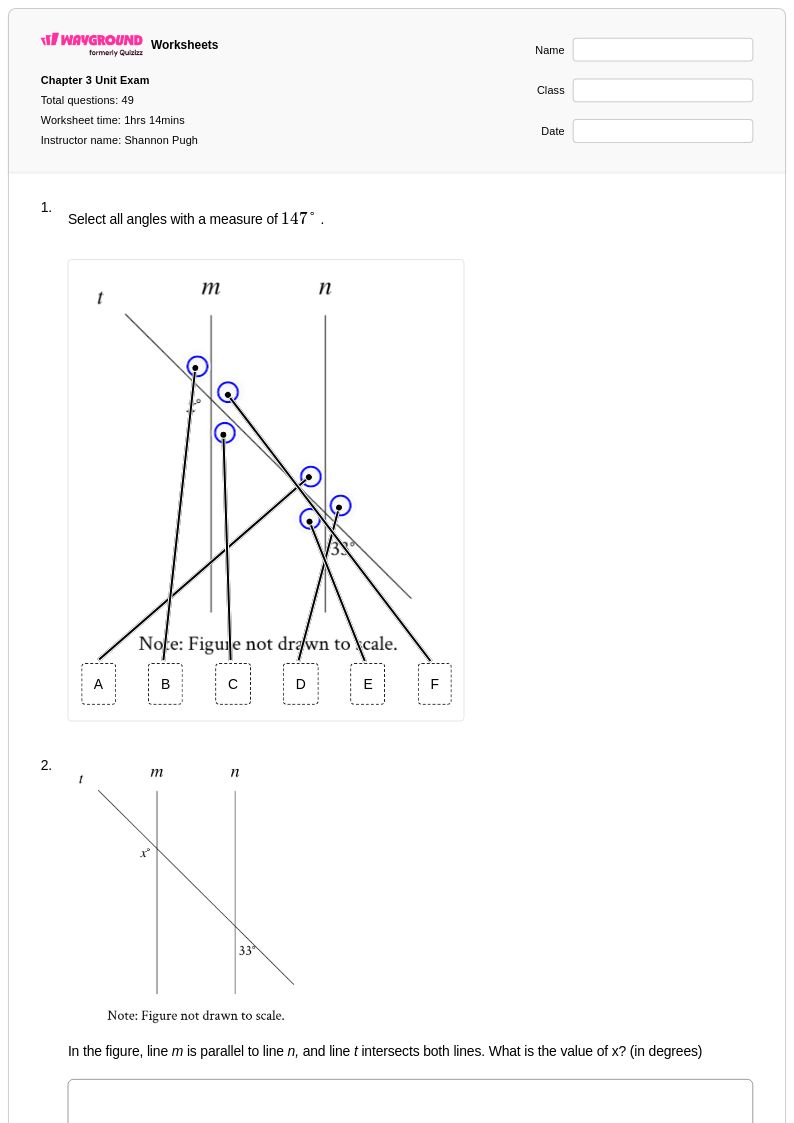
49 คิว
10th
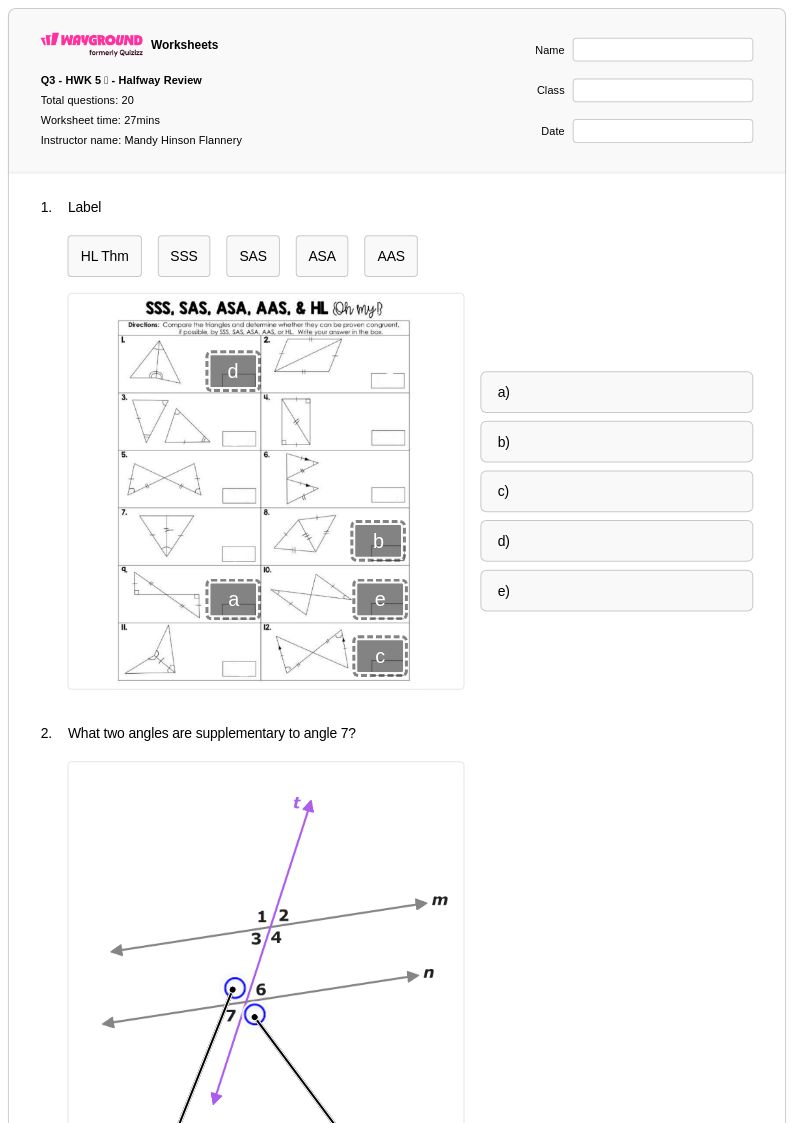
20 คิว
10th

18 คิว
10th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 10
สำรวจแผ่นงาน มุมภายนอกของสามเหลี่ยม ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 10
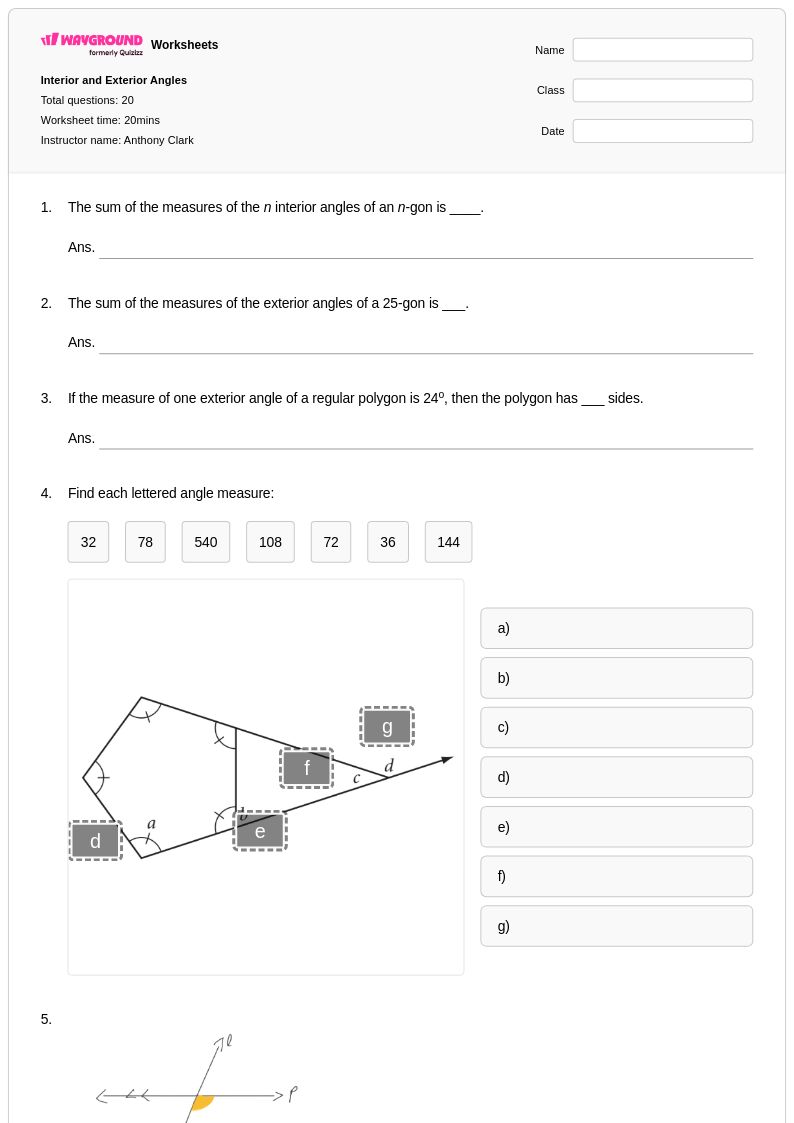
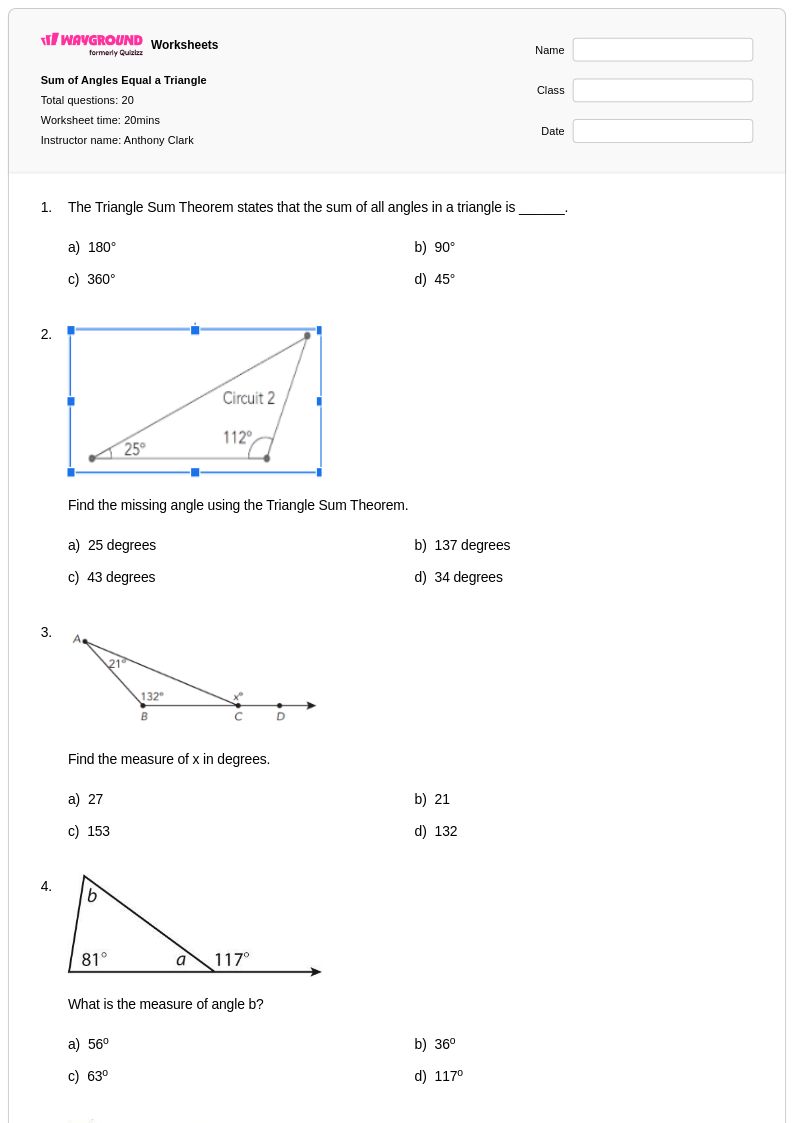
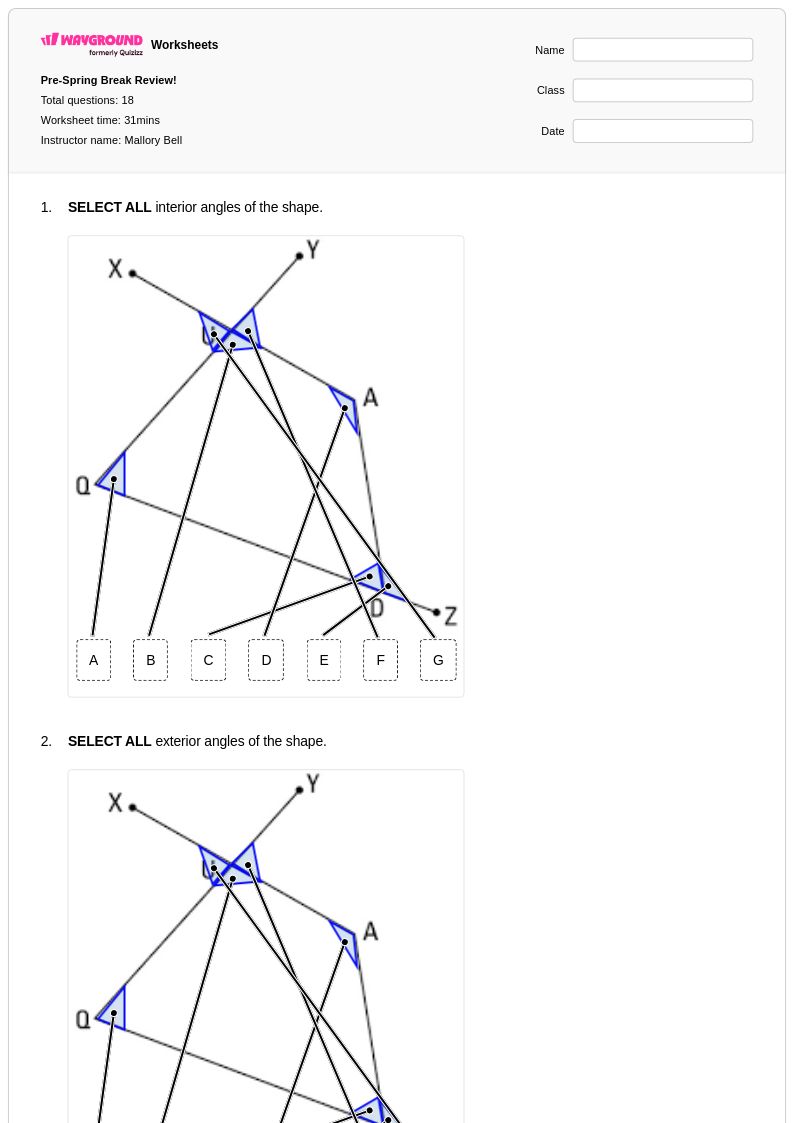
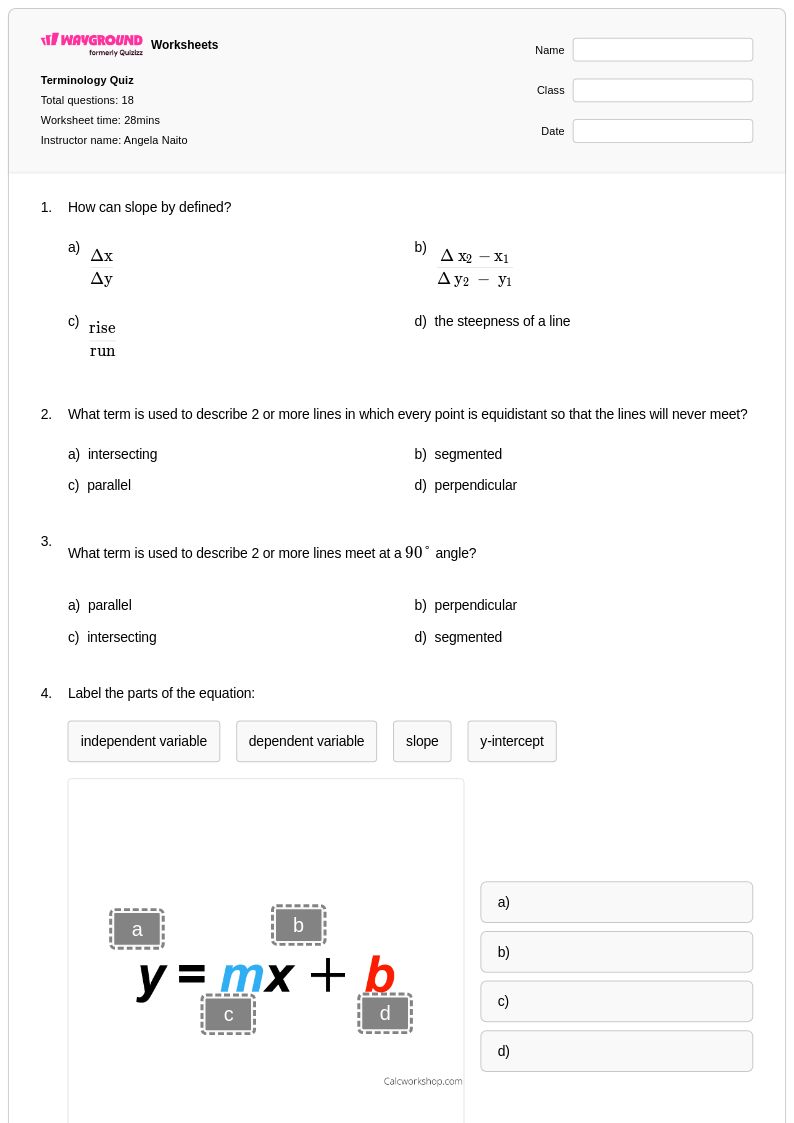
แบบฝึกหัดเรื่องมุมภายนอกของสามเหลี่ยมสำหรับนักเรียนชั้นมัธยมศึกษาปีที่ 4 จาก Wayground (เดิมชื่อ Quizizz) เป็นแบบฝึกหัดที่ครอบคลุมเกี่ยวกับทฤษฎีบทพื้นฐานทางเรขาคณิต แหล่งข้อมูลทางการศึกษาเหล่านี้ช่วยให้นักเรียนเข้าใจแนวคิดที่ว่ามุมภายนอกของสามเหลี่ยมเท่ากับผลรวมของมุมภายในสองมุมที่ไม่ติดกัน ซึ่งจะช่วยเสริมสร้างความเข้าใจเกี่ยวกับความสัมพันธ์เชิงมุมและการให้เหตุผลทางเรขาคณิต แบบฝึกหัดประกอบด้วยโจทย์ฝึกฝนที่หลากหลายซึ่งท้าทายให้นักเรียนคำนวณขนาดมุมที่ไม่ทราบค่า พิสูจน์ความสัมพันธ์ทางเรขาคณิต และประยุกต์ใช้ทฤษฎีบทมุมภายนอกในโจทย์ปัญหาหลายขั้นตอนที่ซับซ้อน แบบฝึกหัดแต่ละชุดมีเฉลยคำตอบโดยละเอียดเพื่อสนับสนุนการเรียนรู้ด้วยตนเองและการประเมินตนเอง พร้อมไฟล์ PDF ที่พิมพ์ได้ฟรี ทำให้เข้าถึงได้ทั้งสำหรับการเรียนการสอนในห้องเรียนและการศึกษาที่บ้าน
Wayground (เดิมชื่อ Quizizz) ช่วยเสริมศักยภาพให้ครูผู้สอนด้วยแหล่งข้อมูลทฤษฎีบทมุมภายนอกที่สร้างโดยครูผู้สอนนับล้านรายการ ซึ่งช่วยลดความซับซ้อนในการวางแผนบทเรียนและการสอนที่แตกต่างกันสำหรับวิชาเรขาคณิตชั้นมัธยมศึกษาปีที่ 4 แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานหลักสูตรและวัตถุประสงค์การเรียนรู้ได้อย่างรวดเร็ว ในขณะที่เครื่องมือปรับแต่งช่วยให้ครูสามารถแก้ไขสื่อที่มีอยู่หรือสร้างชุดแบบฝึกหัดใหม่ที่ปรับให้เหมาะกับความต้องการของนักเรียนได้ แหล่งข้อมูลอเนกประสงค์เหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่พิมพ์ได้และรูปแบบดิจิทัลแบบโต้ตอบ รองรับสภาพแวดล้อมการเรียนรู้และสไตล์การสอนที่หลากหลาย ครูสามารถใช้ชุดแบบฝึกหัดเหล่านี้ได้อย่างมีประสิทธิภาพสำหรับการแนะนำทักษะเบื้องต้น การแก้ไขปัญหาเฉพาะจุดสำหรับนักเรียนที่เรียนรู้ช้า กิจกรรมเสริมสำหรับผู้เรียนที่มีความสามารถสูง และการฝึกฝนอย่างสม่ำเสมอเพื่อเสริมสร้างความเข้าใจในแนวคิดทางเรขาคณิตตลอดปีการศึกษา
