16 T
10th

12 T
9th - 12th
12 T
10th
21 T
9th - 12th
18 T
10th

15 T
9th - 12th
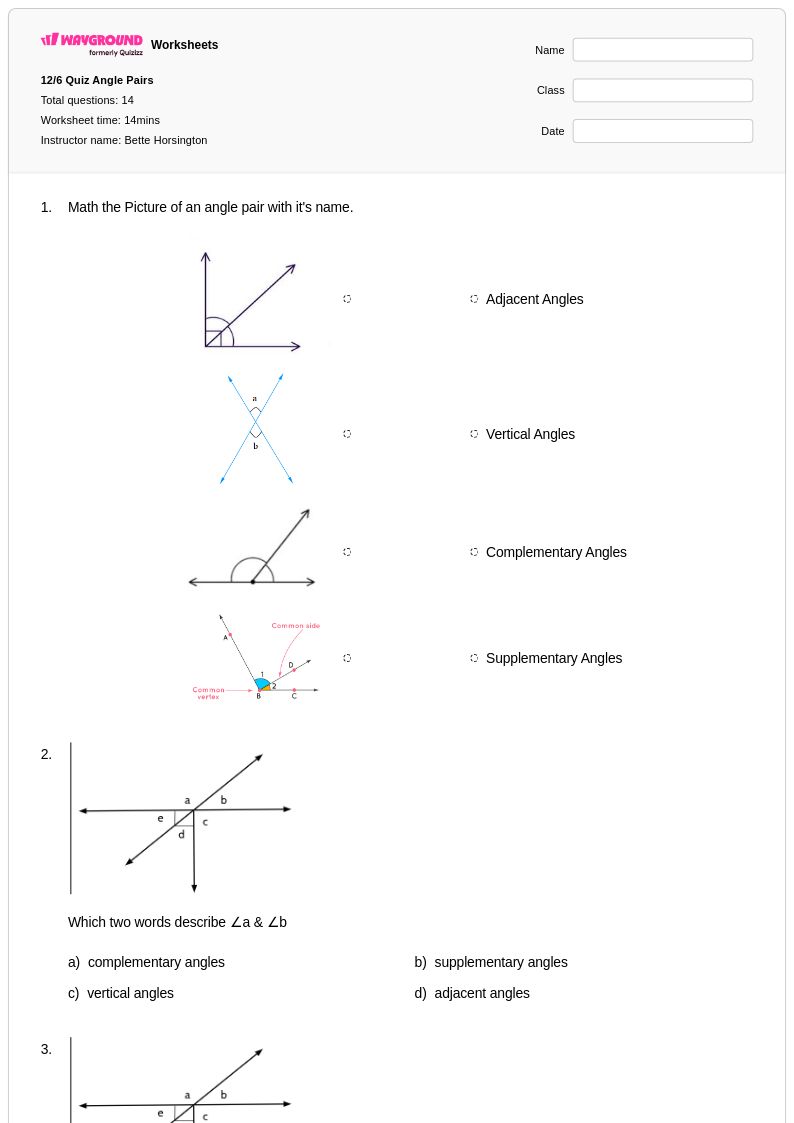
14 T
8th - Uni
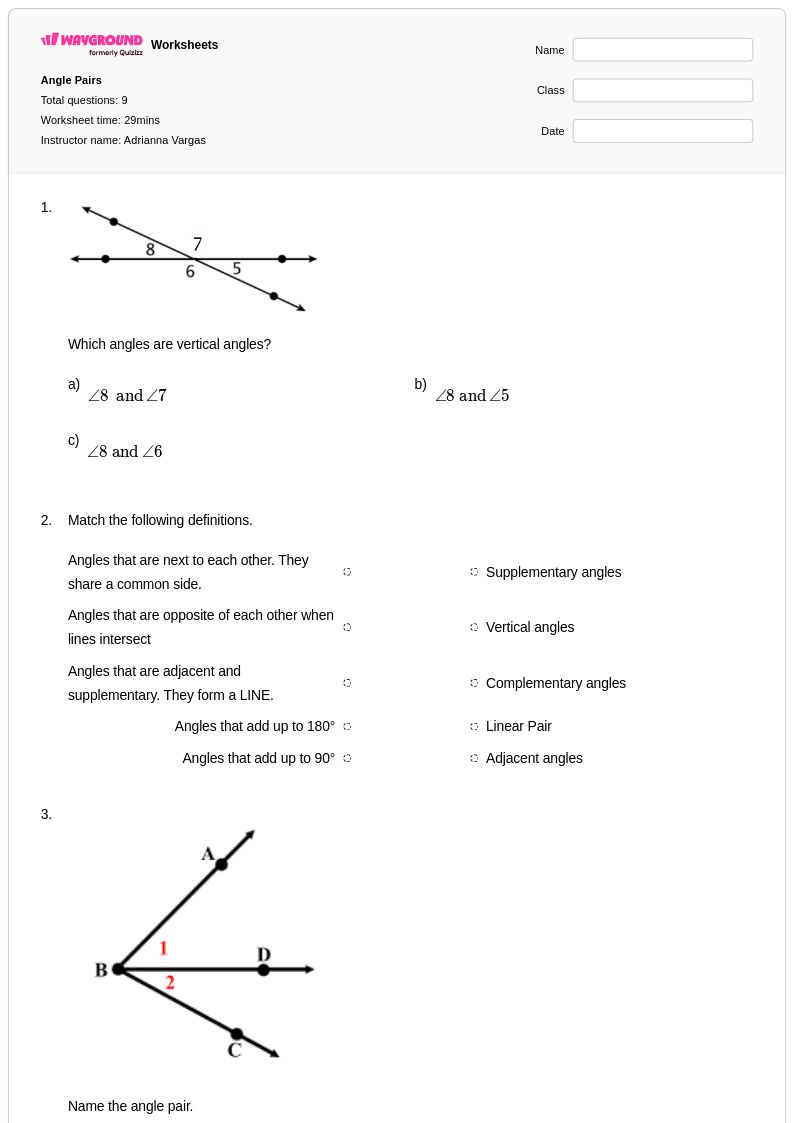
9 T
10th

20 T
9th - 12th

5 T
10th
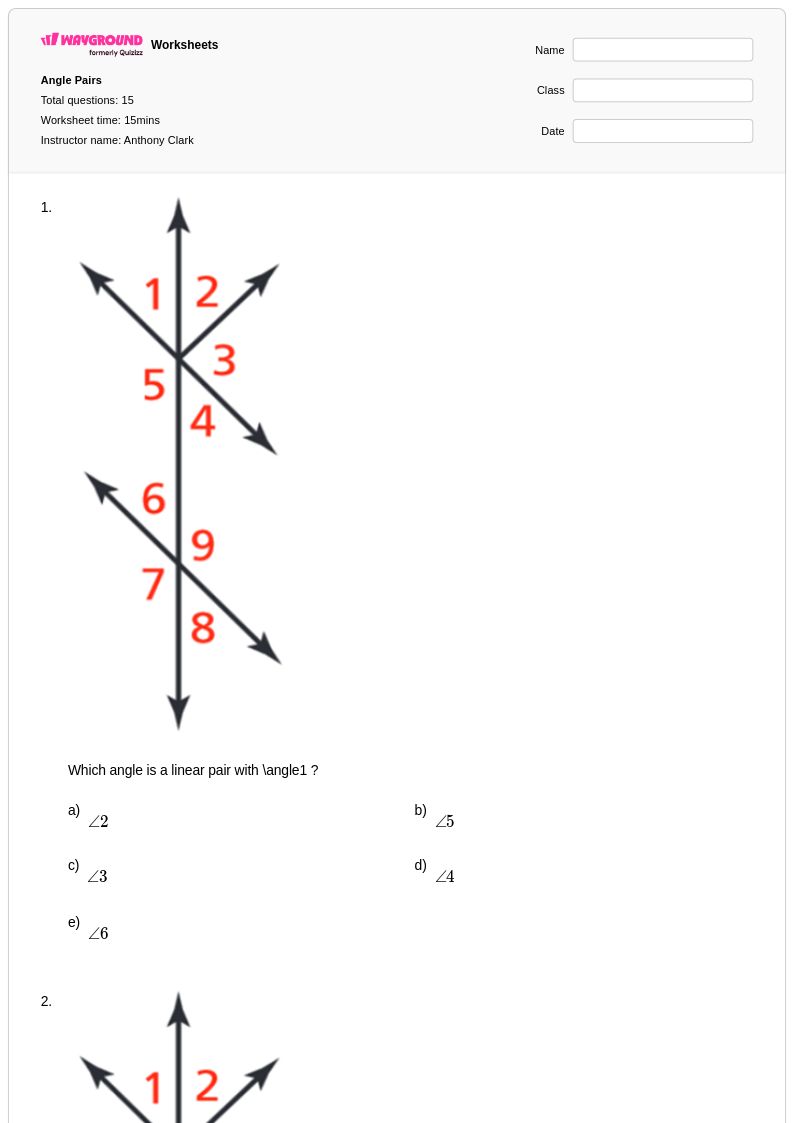
15 T
9th - Uni
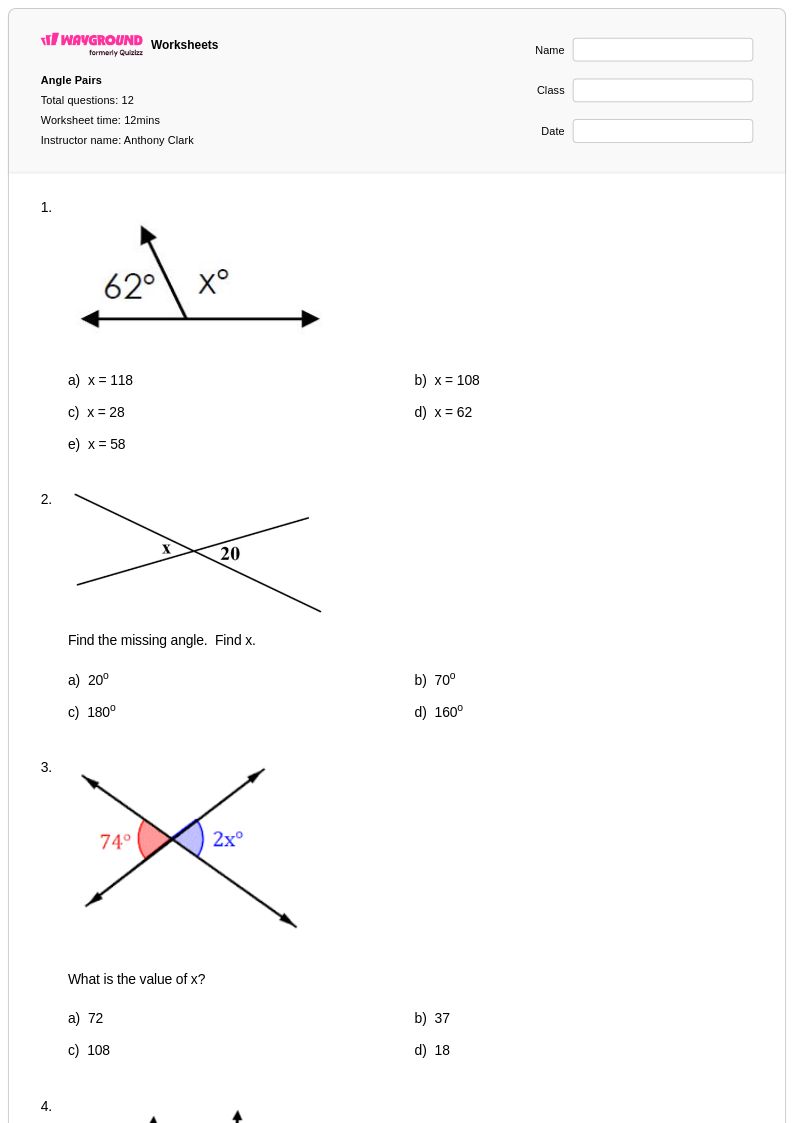
12 T
9th - Uni
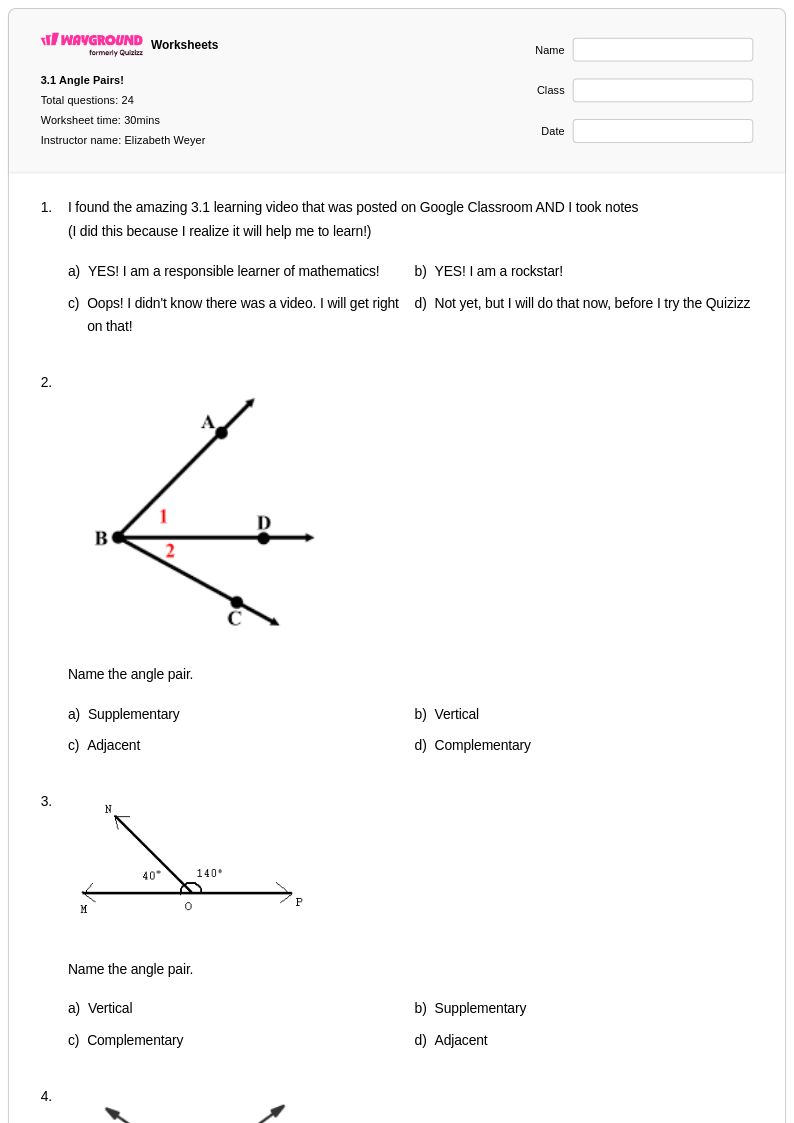
24 T
10th
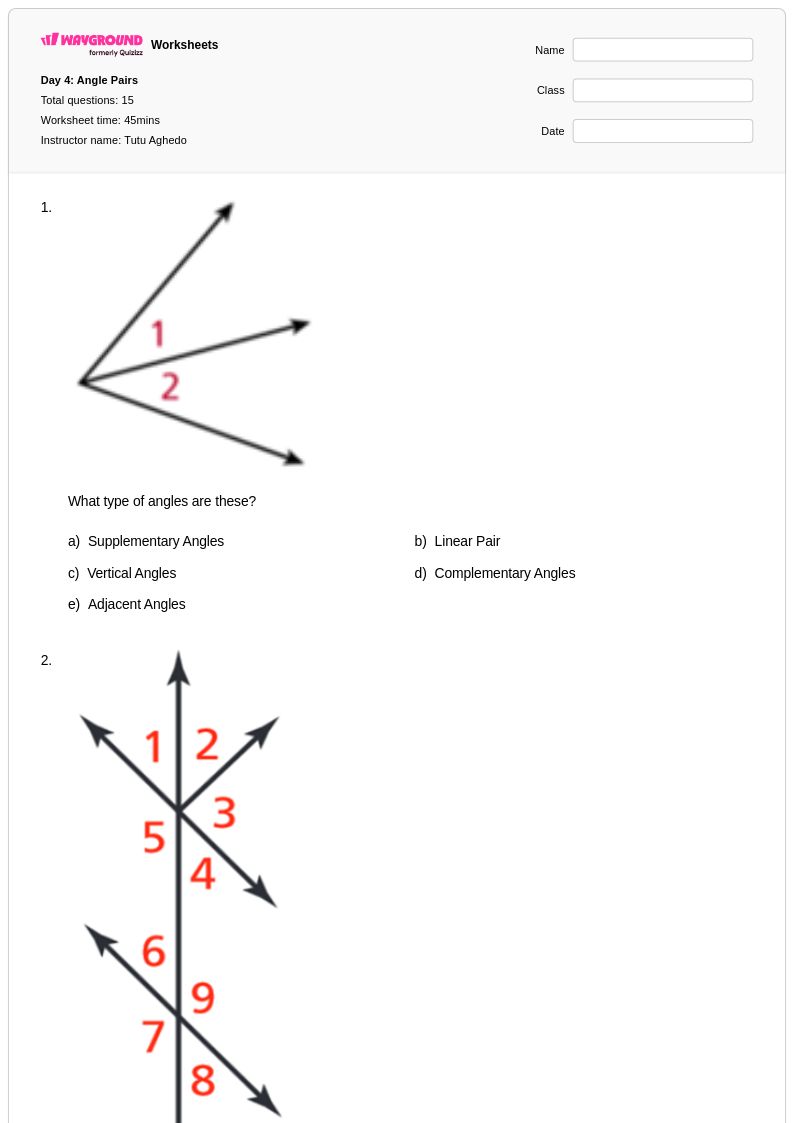
15 T
10th
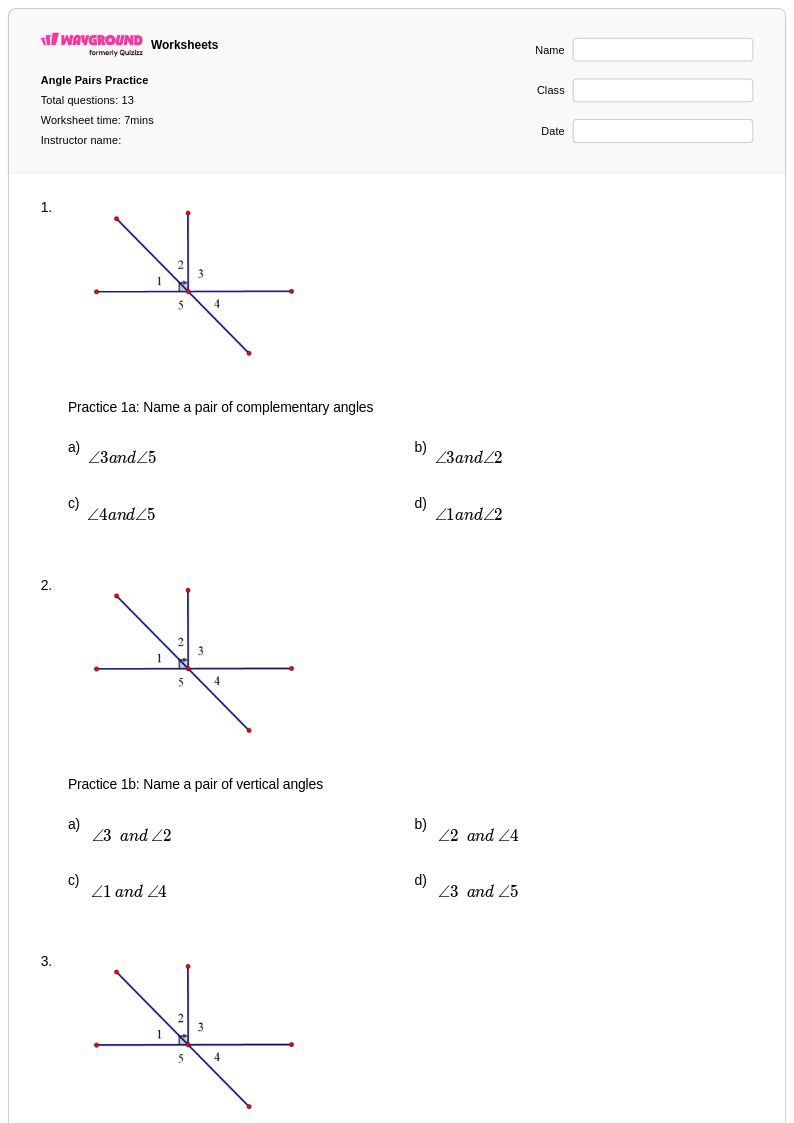
13 T
9th - 12th

20 T
9th - Uni

16 T
9th - 12th
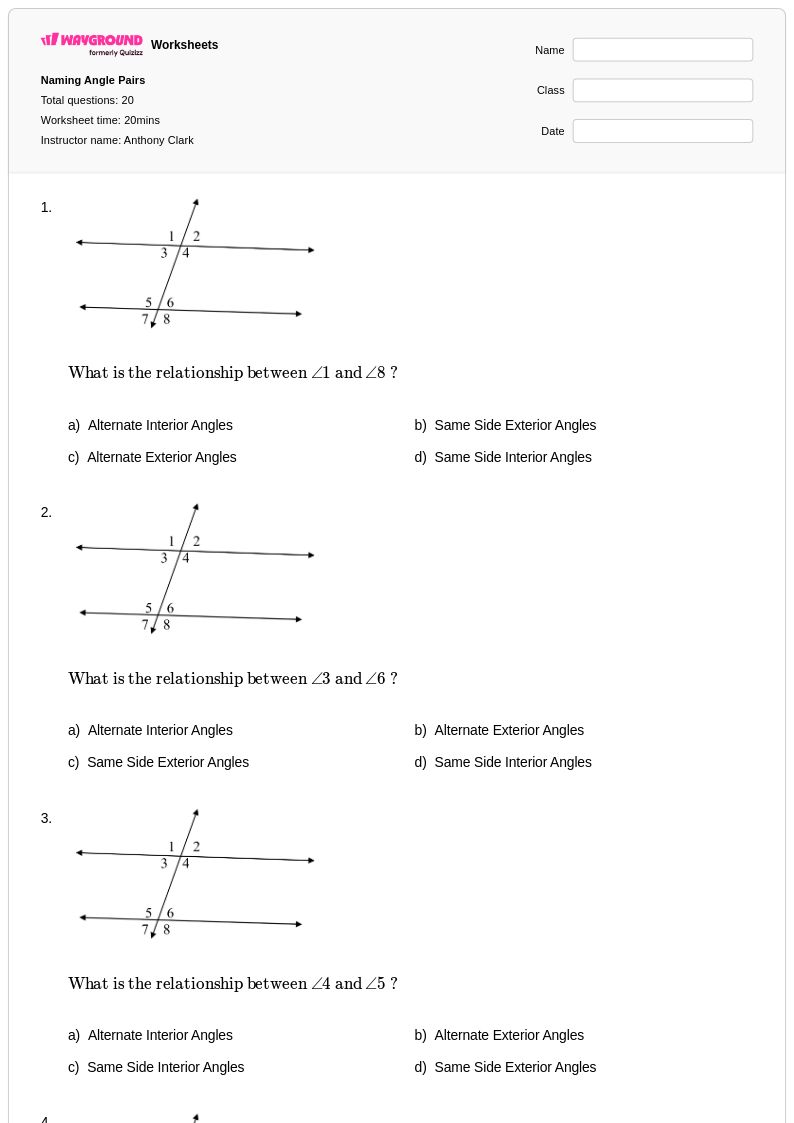
20 T
9th - Uni
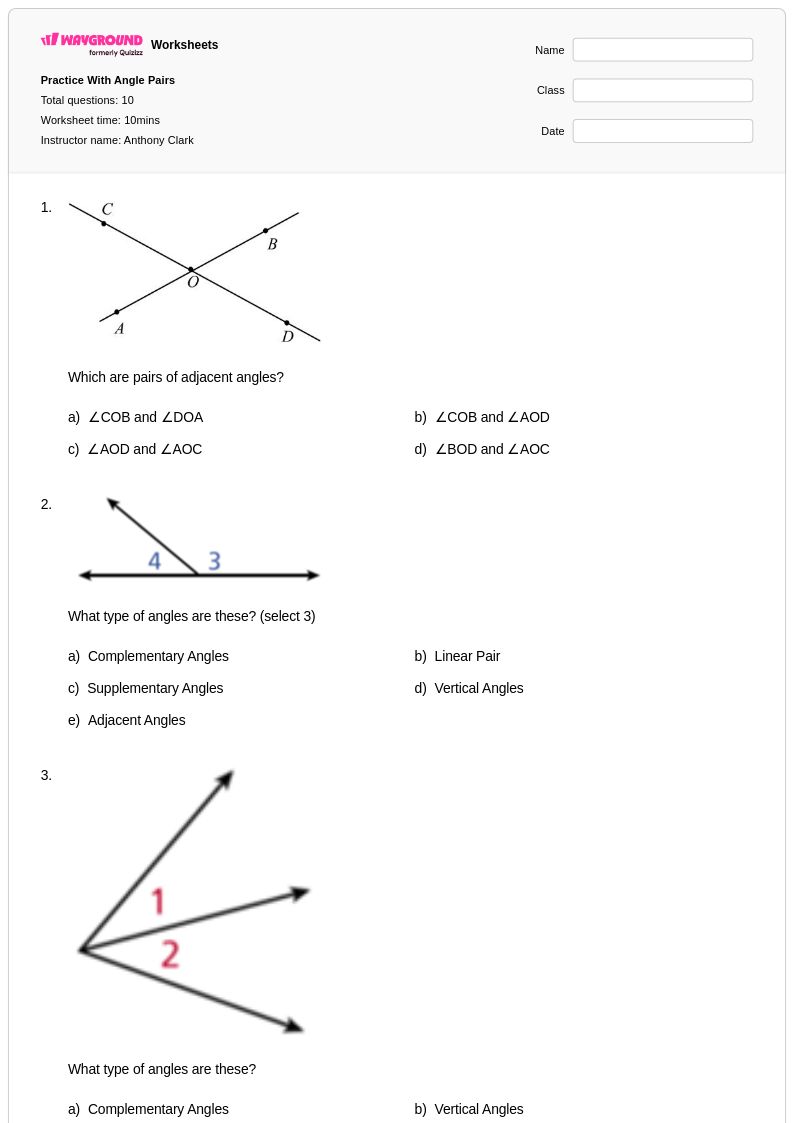
10 T
9th - Uni
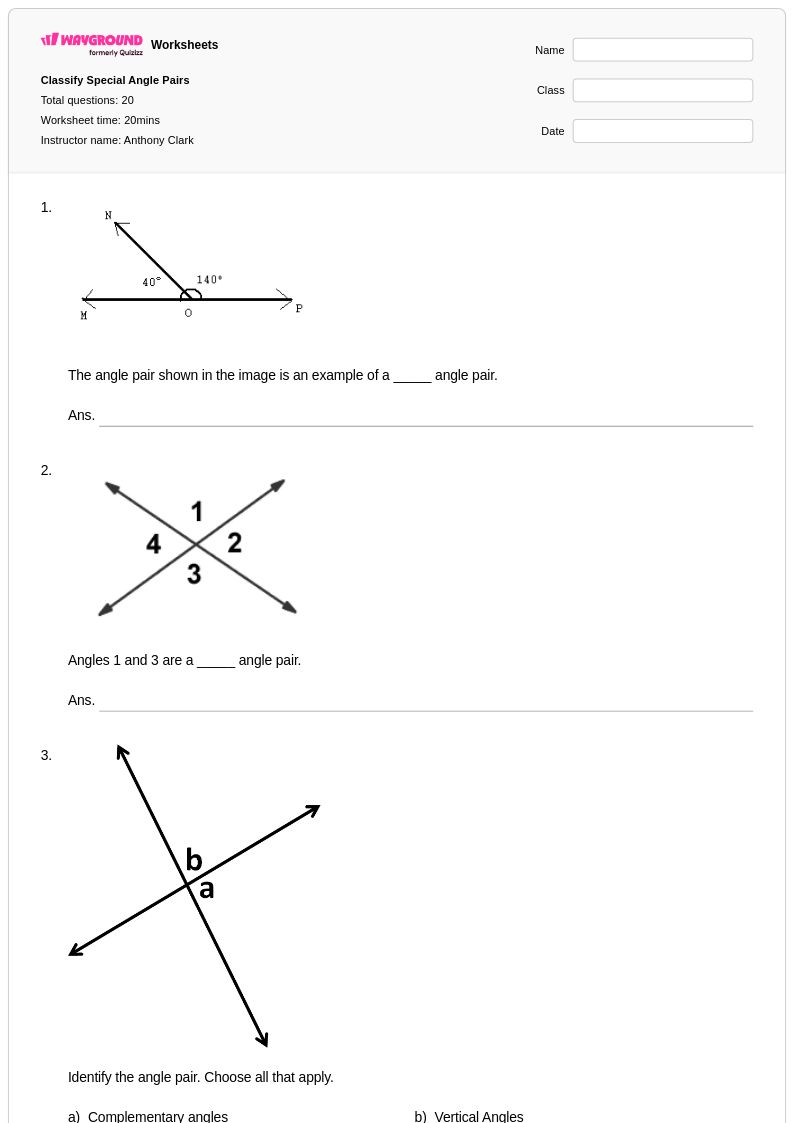
20 T
9th - Uni
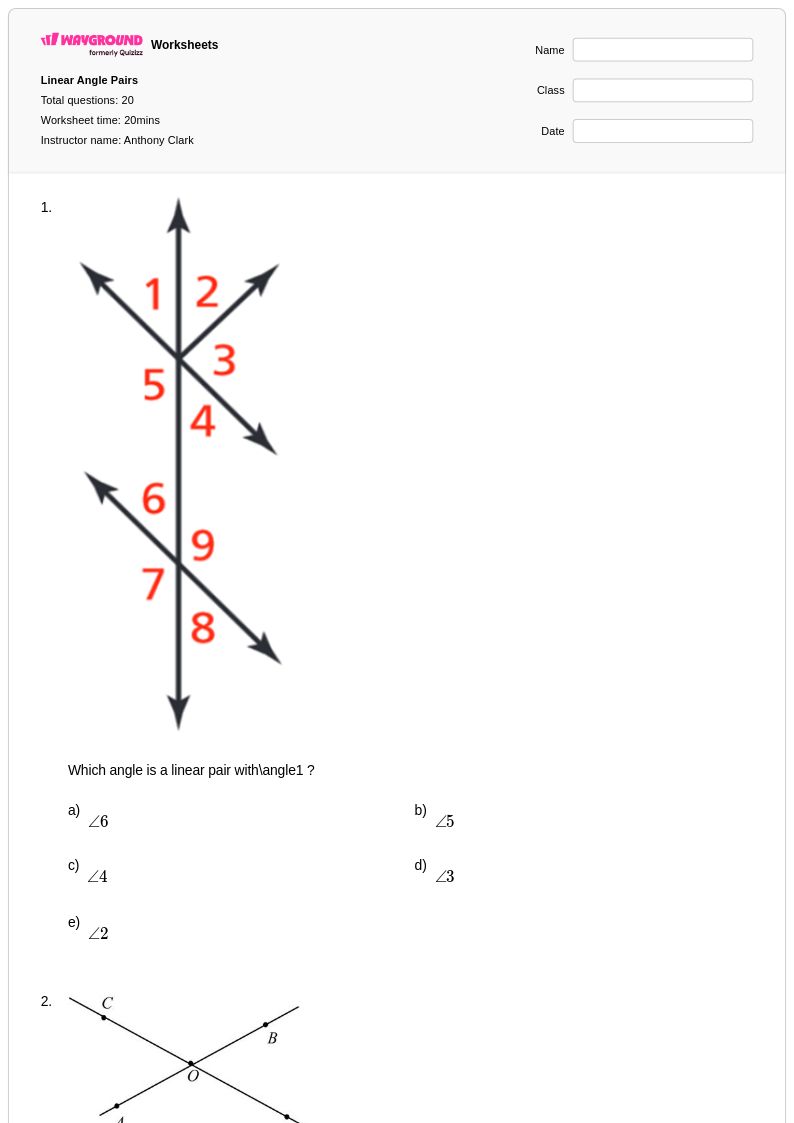
20 T
9th - Uni
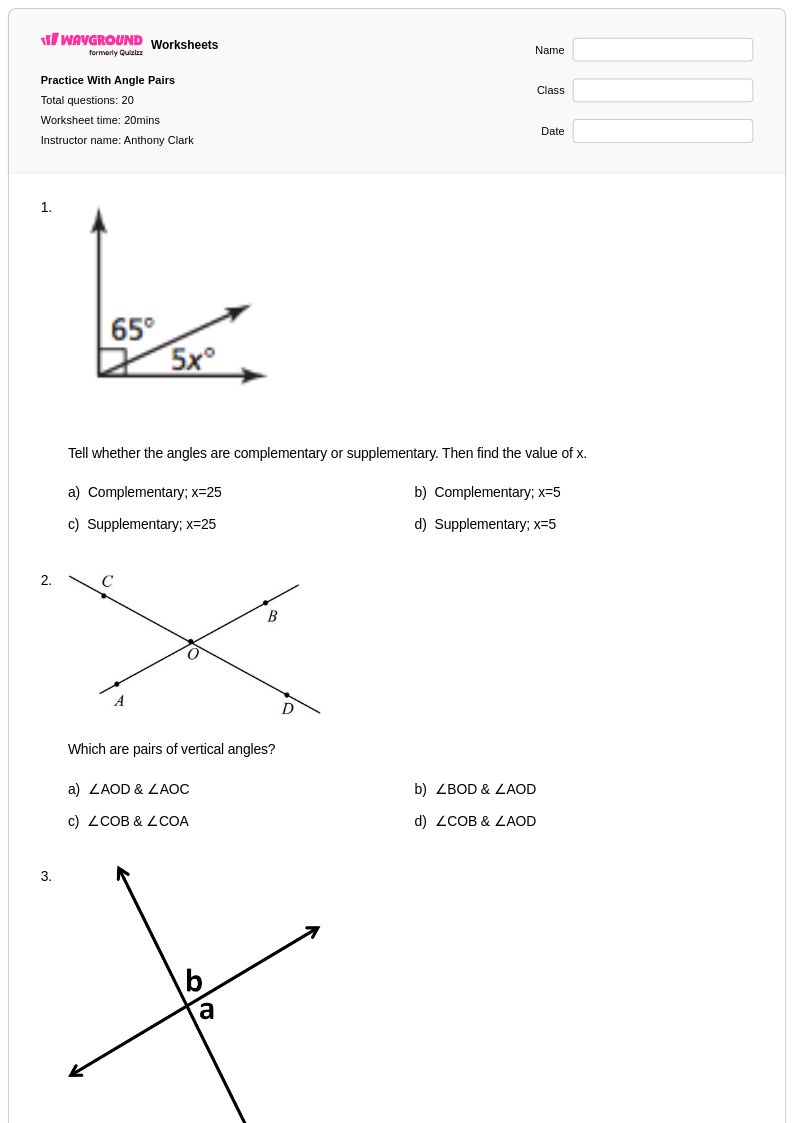
20 T
9th - Uni
20 T
9th - Uni
14 T
9th - 12th
Jelajahi Lembar Kerja Mata Pelajaran Lainnya untuk ระดับ 10
สำรวจแผ่นงาน คู่มุม ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 10
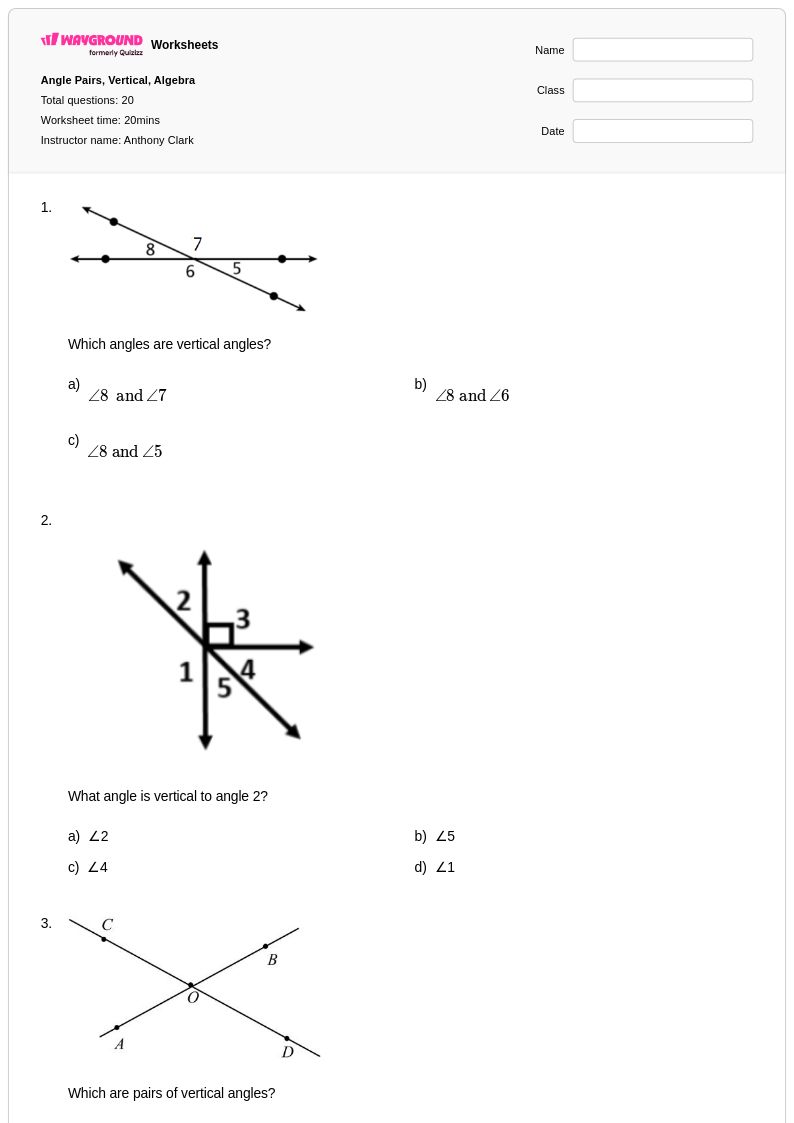
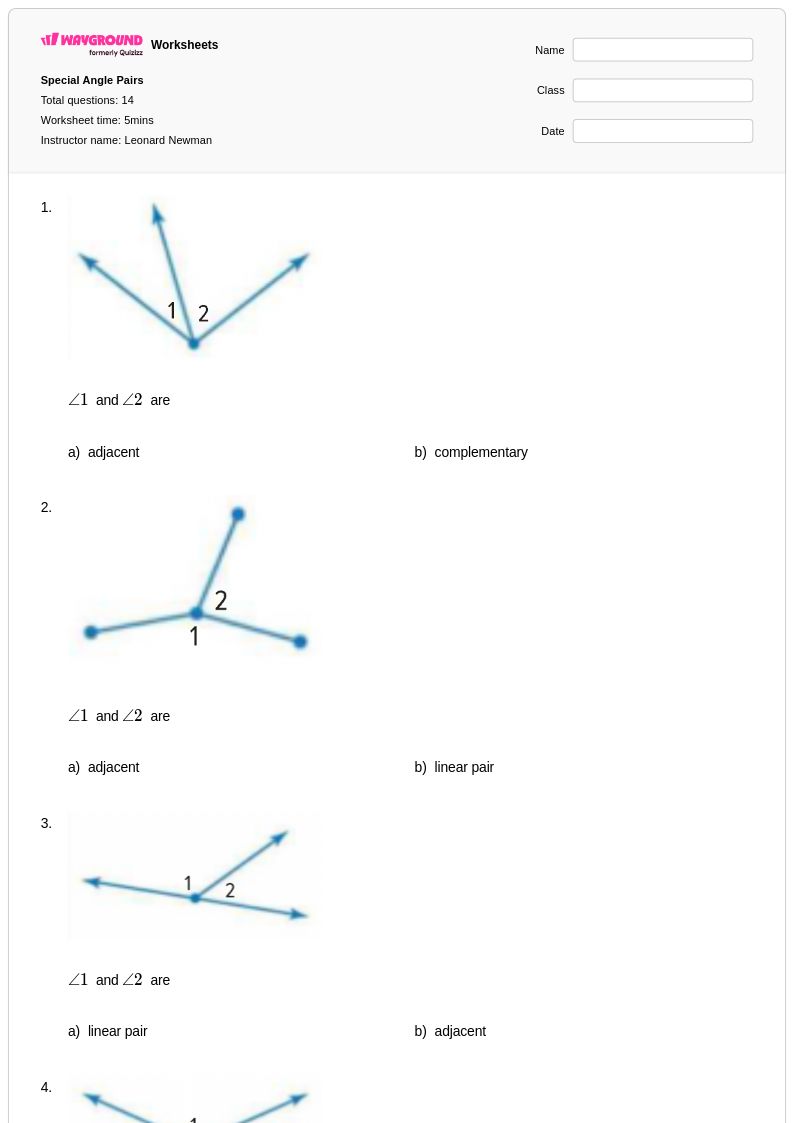
แบบฝึกหัดเรื่องคู่มุมสำหรับนักเรียนชั้นมัธยมศึกษาปีที่ 4 จาก Wayground (เดิมชื่อ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมเกี่ยวกับความสัมพันธ์ทางเรขาคณิตพื้นฐาน ซึ่งเป็นรากฐานของการให้เหตุผลทางคณิตศาสตร์ขั้นสูง แหล่งข้อมูลที่ออกแบบมาอย่างเชี่ยวชาญเหล่านี้ช่วยเสริมสร้างความสามารถของนักเรียนในการระบุ จำแนก และคำนวณขนาดของมุมประกอบ มุมเสริม มุมตรงข้าม มุมประชิด และมุมเส้นตรง ผ่านแบบฝึกหัดที่มีโครงสร้างอย่างรอบคอบ ซึ่งค่อยๆ พัฒนาจากการระบุขั้นพื้นฐานไปจนถึงการคำนวณหลายขั้นตอนที่ซับซ้อน แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียด และมีให้ดาวน์โหลดเป็นไฟล์ PDF ฟรี ช่วยให้ครูสามารถบูรณาการแนวคิดเรื่องคู่มุมเข้ากับหลักสูตรเรขาคณิตได้อย่างราบรื่น พร้อมทั้งให้ข้อเสนอแนะแก่นักเรียนเกี่ยวกับการให้เหตุผลทางคณิตศาสตร์และความถูกต้องในการคำนวณได้ทันที
Wayground (เดิมชื่อ Quizizz) ช่วยให้ครูเข้าถึงแหล่งข้อมูลคู่มุมที่สร้างโดยครูผู้สอนนับล้านรายการ ซึ่งมีระบบค้นหาและกรองข้อมูลที่มีประสิทธิภาพ ช่วยให้ค้นพบสื่อการเรียนรู้ที่สอดคล้องกับวัตถุประสงค์การเรียนรู้และมาตรฐานหลักสูตรได้อย่างรวดเร็ว เครื่องมือการปรับระดับความยากง่ายที่ซับซ้อนของแพลตฟอร์มนี้ ช่วยให้ผู้สอนสามารถปรับแต่งแบบฝึกหัดให้เหมาะสมกับระดับความสามารถที่แตกต่างกันในห้องเรียนระดับชั้นมัธยมศึกษาปีที่ 4 ได้ ในขณะที่รูปแบบไฟล์ PDF ที่พิมพ์ได้และเวอร์ชันดิจิทัลแบบโต้ตอบได้นั้น ยืดหยุ่นและรองรับสภาพแวดล้อมการสอนที่หลากหลายและความต้องการของนักเรียนได้ดี คุณสมบัติที่ครอบคลุมเหล่านี้ช่วยให้การวางแผนบทเรียนง่ายขึ้น โดยการจัดเตรียมสื่อการเรียนรู้ที่พร้อมใช้งานสำหรับการฝึกฝนทักษะ การแก้ไขปัญหาเฉพาะจุดสำหรับผู้เรียนที่มีปัญหา และโอกาสในการเสริมสร้างความรู้สำหรับนักเรียนที่มีความสามารถสูง ทำให้มั่นใจได้ว่านักเรียนชั้นมัธยมศึกษาปีที่ 4 ทุกคนจะสามารถเชี่ยวชาญความสัมพันธ์ของคู่มุมที่สำคัญ ซึ่งจำเป็นต่อความสำเร็จในหลักสูตรเรขาคณิตและตรีโกณมิติระดับสูง
