
10 คิว
8th - Uni

66 คิว
8th
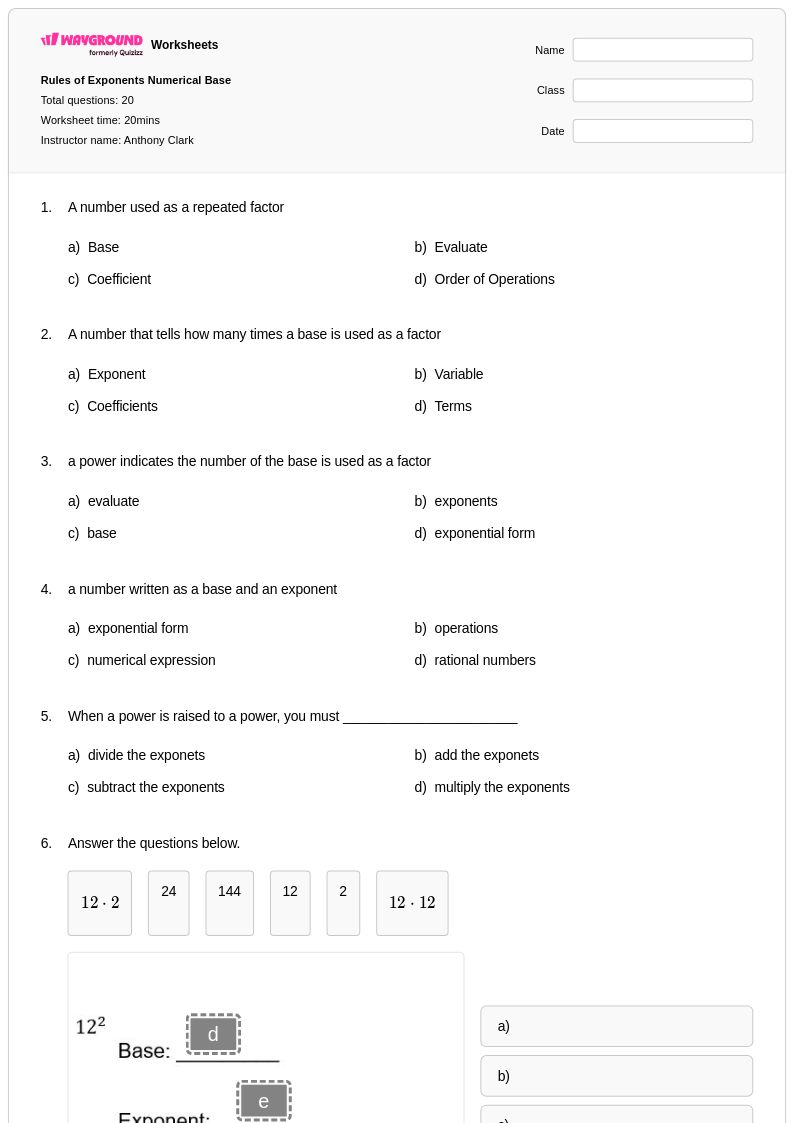
20 คิว
8th - Uni

20 คิว
8th - 9th

22 คิว
8th

10 คิว
8th

15 คิว
8th

12 คิว
8th

20 คิว
8th

34 คิว
8th

15 คิว
8th

25 คิว
8th

22 คิว
8th
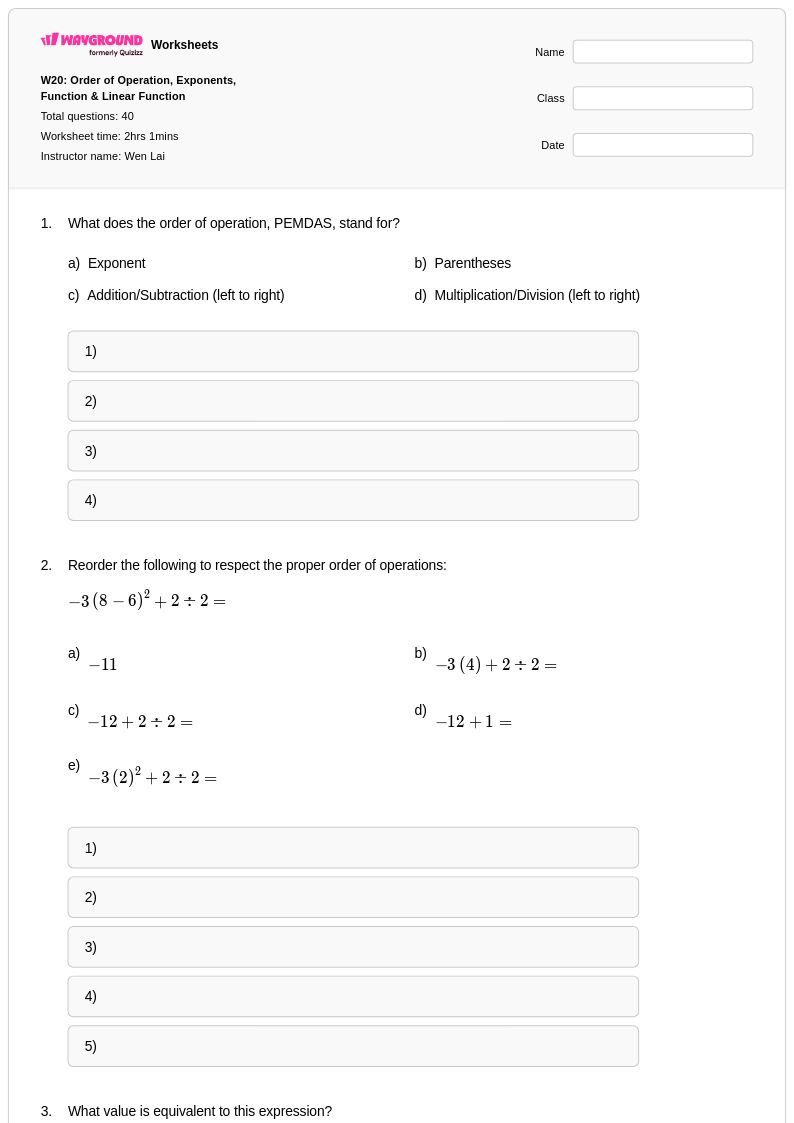
40 คิว
8th

18 คิว
6th - Uni

11 คิว
8th - 9th

10 คิว
8th

10 คิว
8th

25 คิว
8th

30 คิว
6th - Uni

20 คิว
6th - Uni

14 คิว
8th

20 คิว
8th

14 คิว
8th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 8
สำรวจแผ่นงาน การดำเนินการยกกำลัง ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 8
การคำนวณเลขยกกำลังเป็นแนวคิดทางคณิตศาสตร์ที่สำคัญสำหรับนักเรียนชั้น ม.2 ซึ่งต้องอาศัยความเข้าใจในกฎพื้นฐานที่ควบคุมการทำงานร่วมกันของเลขยกกำลังและฐานในนิพจน์พีชคณิต ชุดแบบฝึกหัดการคำนวณเลขยกกำลังที่ครอบคลุมของ Wayground ช่วยให้นักเรียนพัฒนาทักษะที่จำเป็นได้อย่างคล่องแคล่ว รวมถึงการคูณและการหารเลขยกกำลังที่มีฐานเดียวกัน การยกกำลังซ้ำ และการทำงานกับเลขยกกำลังติดลบและศูนย์ แบบฝึกหัดที่ออกแบบมาอย่างพิถีพิถันเหล่านี้จะนำผู้เรียนไปสู่การสำรวจกฎของเลขยกกำลังอย่างเป็นระบบ เสริมสร้างความเข้าใจเชิงแนวคิดพร้อมทั้งสร้างความแม่นยำในการคำนวณ แบบฝึกหัดแต่ละชุดมีเฉลยคำตอบโดยละเอียด ช่วยให้สามารถศึกษาด้วยตนเองและเรียนรู้ได้จากผู้สอน พร้อมไฟล์ PDF ที่พิมพ์ได้ฟรี เพื่อให้เข้าถึงได้ในสภาพแวดล้อมการเรียนรู้ที่หลากหลาย
คลังแบบฝึกหัดที่กว้างขวางของ Wayground รวบรวมจากแหล่งข้อมูลนับล้านที่สร้างโดยครูผู้สอน ซึ่งออกแบบมาโดยเฉพาะเพื่อสนับสนุนการสอนที่มีประสิทธิภาพเกี่ยวกับการคำนวณเลขยกกำลังและแนวคิดทางคณิตศาสตร์ที่เกี่ยวข้อง แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาสื่อการเรียนการสอนที่สอดคล้องกับมาตรฐานและวัตถุประสงค์การเรียนรู้ได้อย่างรวดเร็ว ในขณะที่เครื่องมือการปรับระดับความยากง่ายในตัว ช่วยให้สามารถปรับแต่งสื่อการเรียนการสอนได้อย่างราบรื่นสำหรับระดับความสามารถที่แตกต่างกันในห้องเรียนระดับชั้น ม.2 ครูสามารถเข้าถึงแหล่งข้อมูลเหล่านี้ได้ทั้งในรูปแบบสิ่งพิมพ์และดิจิทัล รวมถึงไฟล์ PDF ที่ดาวน์โหลดได้ ซึ่งช่วยให้การวางแผนและดำเนินการสอนมีความยืดหยุ่นมากขึ้น แนวทางที่ครอบคลุมนี้สนับสนุนการแก้ไขปัญหาอย่างตรงจุดสำหรับนักเรียนที่เรียนรู้ช้า ให้โอกาสในการเสริมสร้างความรู้สำหรับนักเรียนที่มีความสามารถสูง และมอบการฝึกฝนทักษะอย่างสม่ำเสมอซึ่งช่วยเสริมสร้างความเข้าใจพื้นฐานเกี่ยวกับความสัมพันธ์แบบเลขยกกำลัง ซึ่งจำเป็นต่อความสำเร็จในวิชาคณิตศาสตร์ระดับสูง
